人教B版(2019)高中数学选择性必修第一册 2.3.1 圆的标准方程(共22张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 2.3.1 圆的标准方程(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 837.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览








文档简介
2.3.1 圆的标准方程
核心素养
1.掌握圆的定义及标准方程.(数学抽象)
2.能根据圆心、半径写出圆的标准方程,并能解决一些简单的实际问题.(数学模型)
3.会用待定系数法求圆的标准方程.(数学运算)
4.能借助圆的几何性质处理与圆心及半径有关的问题.(直观想象)
思维脉络
激趣诱思
知识点拨
拉达尔公路隧道位于挪威西部,是世界上最长的公路隧道.拉达尔隧道位于挪威西部的拉达尔和艾于兰之间,全长24.51千米.于1995年3月开始动工兴建,2000年11月27日正式通车.隧道
中也蕴含着丰富的数学知识,比如,隧道横截面可近似看成半圆形,测出相关数据可以解决车辆能否通过的问题.
提出问题已知隧道的截面是半径为4 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?
提示:以某一截面半圆的圆心为坐标原点,半圆的直径AB所在直线为x轴,建立直角坐标系,则半圆的方程为x2+y2=16(y≥0),将x=2.7代
即在离隧道中心线2.7 m处,隧道的高度低于货车的高度,因此货车不能驶入这个隧道.
激趣诱思
知识点拨
1.圆的定义
平面内到一定点的距离等于定长的点的集合是圆,其中定点是圆心,定长是圆的半径.
微思考
平面内到一个定点的距离小于或等于定长的点的集合是什么?
提示:是一个以定点为圆心,以定长为半径的圆面.
激趣诱思
知识点拨
2.圆的标准方程
一般地,如果平面直角坐标系中☉C的圆心为C(a,b),半径为r(r>0),设M(x,y)为平面直角坐标系中任意一点,则点M在☉C上的充要条件是|CM|=r,即 =r,两边平方,得(x-a)2+(y-b)2=r2,通常称为圆的标准方程.
激趣诱思
知识点拨
微判断
(1)(x-a)2+(y-b)2=r2一定表示圆的方程.( )
直线y=b下方的半圆弧.( )
答案:(1)× (2)√
微思考
在平面直角坐标系中,圆是函数的图像吗?
提示:根据函数知识,对于平面直角坐标系中的某一曲线,如果垂直于x轴的直线与此曲线至多有一个交点,那么这条曲线是函数的图像,否则,不是函数的图像.对于平面直角坐标系中的圆,垂直于x轴的直线与其至多有两个交点,因此圆不是函数的图像.
激趣诱思
知识点拨
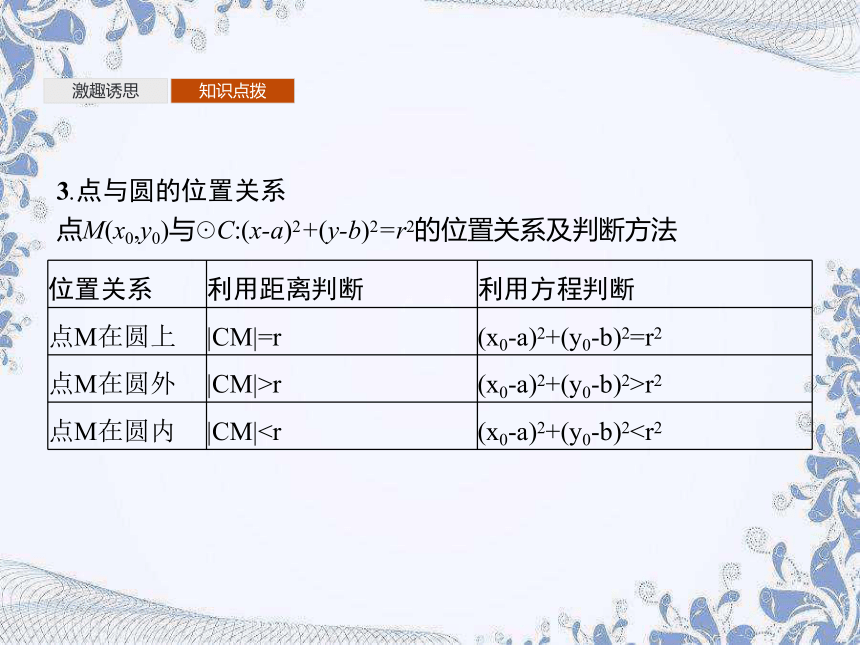
3.点与圆的位置关系
点M(x0,y0)与☉C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
利用方程判断
点M在圆上
|CM|=r
(x0-a)2+(y0-b)2=r2
点M在圆外
|CM|>r
(x0-a)2+(y0-b)2>r2
点M在圆内
|CM| (x0-a)2+(y0-b)2激趣诱思
知识点拨
微练习
点P(1,3)与圆x2+y2=24的位置关系是( )
A.在圆外
B.在圆内
C.在圆上
D.不确定
答案:B
探究一
探究二
素养形成
当堂检测
求圆的标准方程
例1(1)圆心在点C(2,1),半径长是 的圆的标准方程为 .?
(2)圆心在点C(8,-3),且过点P(5,1)的圆的标准方程为 .?
(3)已知两点A(-1,-3),B(3,a),以线段AB为直径的圆经过原点,则该圆的标准方程为 .?
探究一
探究二
素养形成
当堂检测
因为以线段AB为直径的圆经过原点,
故(0,0)代入①成立,解得a=-1.
故圆的标准方程为(x-1)2+(y+2)2=5.
答案:(1)(x-2)2+(y-1)2=3
(2)(x-8)2+(y+3)2=25
(3)(x-1)2+(y+2)2=5
探究一
探究二
素养形成
当堂检测
反思感悟 1.确定圆的标准方程只需确定圆心坐标和半径,因此用直接法求圆的标准方程时,要首先求出圆心坐标和半径,然后直接写出圆的标准方程.
2.确定圆心和半径时,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”,“两条弦的中垂线的交点必为圆心”等.
探究一
探究二
素养形成
当堂检测
变式训练(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x+1)2+(y+2)2=100
B.(x-1)2+(y-2)2=100
C.(x+1)2+(y+2)2=25
D.(x-1)2+(y-2)2=25
(2)与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程为 .?
探究一
探究二
素养形成
当堂检测
解析:(1)∵AB为直径,∴AB的中点(1,2)为圆心,
∴该圆的标准方程为(x-1)2+(y-2)2=25.
(2)∵圆心坐标为(-5,-3),又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为(x+5)2+(y+3)2=25.
答案:(1)D (2)(x+5)2+(y+3)2=25
探究一
探究二
素养形成
当堂检测
点与圆的位置关系
例2已知在平面直角坐标系中有A(0,1),B(2,1),C(3,4),D(-1,2)四点,这四点能否在同一个圆上,为什么?
分析先确定出过其中三点的一个圆的方程,再验证第四个点是否在这个圆上,即可得出答案.
所以,经过A,B,C三点的圆的标准方程是(x-1)2+(y-3)2=5.
把点D的坐标(-1,2)代入上述圆的方程,得(-1-1)2+(2-3)2=5.
所以,点D在经过A,B,C三点的圆上,即A,B,C,D四点能在同一个圆上.
探究一
探究二
素养形成
当堂检测
反思感悟 判断点P(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系有几何法和代数法两种:
(1)对于几何法,主要是利用点与圆心的距离与半径比较大小;
(2)对于代数法,主要把点的坐标代入圆的标准方程,左端与r2比较.
延伸探究 试求过三点A(0,1),B(2,1),C(3,4)的圆的方程,并且判断点(3,6)与所求圆的关系.
解:所求方程同例题中的结论(x-1)2+(y-3)2=5.
经判断,因为点(3,6)代入圆方程左边可得(3-1)2+(6-3)2=13>5,因此点(3,6)在该圆外.
探究一
探究二
素养形成
当堂检测
一题多解——待定系数法与几何法求圆的标准方程
案例 求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
归纳提升(1)待定系数法求圆的标准方程的一般步骤
(2)几何法即是利用平面几何知识,求出圆心和半径,然后写出圆的标准方程.
(3)有时待定系数法和几何法交叉使用,体现数形结合的数学思想.
探究一
探究二
素养形成
当堂检测
1.圆心为(3,1),半径为5的圆的标准方程是( )
A.(x+3)2+(y+1)2=5 B.(x+3)2+(y+1)2=25
C.(x-3)2+(y-1)2=5 D.(x-3)2+(y-1)2=25
答案:D
2.若点(5a+1,12a)在圆(x-1)2+y2=1的内部,则实数a满足( )
答案:D
探究一
探究二
素养形成
当堂检测
3.圆心在y轴上,半径为1,且过点(1,2)的圆的标准方程是( )
A.x2+(y-2)2=1 B.x2+(y+2)2=1
C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1
解析:方法一:直接法
∴b=2,
∴圆的标准方程是x2+(y-2)2=1.
方法二:数形结合法
作图(如图),根据点(1,2)到圆心的距离为1易知,
圆心为(0,2),故圆的标准方程是x2+(y-2)2=1.
答案:A
探究一
探究二
素养形成
当堂检测
4.圆(x-3)2+(y+1)2=1关于直线x+y-3=0对称的圆的标准方程是 .?
解析:设圆心A(3,-1)关于直线x+y-3=0对称的点B的坐标为(a,b),
故所求圆的标准方程为(x-4)2+y2=1.
答案:(x-4)2+y2=1
探究一
探究二
素养形成
当堂检测
5.求过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的标准方程.
解:设圆的标准方程为(x-a)2+(y-b)2=r2,
根据已知条件可得
所以所求圆的标准方程为(x-1)2+(y-1)2=4.
核心素养
1.掌握圆的定义及标准方程.(数学抽象)
2.能根据圆心、半径写出圆的标准方程,并能解决一些简单的实际问题.(数学模型)
3.会用待定系数法求圆的标准方程.(数学运算)
4.能借助圆的几何性质处理与圆心及半径有关的问题.(直观想象)
思维脉络
激趣诱思
知识点拨
拉达尔公路隧道位于挪威西部,是世界上最长的公路隧道.拉达尔隧道位于挪威西部的拉达尔和艾于兰之间,全长24.51千米.于1995年3月开始动工兴建,2000年11月27日正式通车.隧道
中也蕴含着丰富的数学知识,比如,隧道横截面可近似看成半圆形,测出相关数据可以解决车辆能否通过的问题.
提出问题已知隧道的截面是半径为4 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?
提示:以某一截面半圆的圆心为坐标原点,半圆的直径AB所在直线为x轴,建立直角坐标系,则半圆的方程为x2+y2=16(y≥0),将x=2.7代
即在离隧道中心线2.7 m处,隧道的高度低于货车的高度,因此货车不能驶入这个隧道.
激趣诱思
知识点拨
1.圆的定义
平面内到一定点的距离等于定长的点的集合是圆,其中定点是圆心,定长是圆的半径.
微思考
平面内到一个定点的距离小于或等于定长的点的集合是什么?
提示:是一个以定点为圆心,以定长为半径的圆面.
激趣诱思
知识点拨
2.圆的标准方程
一般地,如果平面直角坐标系中☉C的圆心为C(a,b),半径为r(r>0),设M(x,y)为平面直角坐标系中任意一点,则点M在☉C上的充要条件是|CM|=r,即 =r,两边平方,得(x-a)2+(y-b)2=r2,通常称为圆的标准方程.
激趣诱思
知识点拨
微判断
(1)(x-a)2+(y-b)2=r2一定表示圆的方程.( )
直线y=b下方的半圆弧.( )
答案:(1)× (2)√
微思考
在平面直角坐标系中,圆是函数的图像吗?
提示:根据函数知识,对于平面直角坐标系中的某一曲线,如果垂直于x轴的直线与此曲线至多有一个交点,那么这条曲线是函数的图像,否则,不是函数的图像.对于平面直角坐标系中的圆,垂直于x轴的直线与其至多有两个交点,因此圆不是函数的图像.
激趣诱思
知识点拨
3.点与圆的位置关系
点M(x0,y0)与☉C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
利用方程判断
点M在圆上
|CM|=r
(x0-a)2+(y0-b)2=r2
点M在圆外
|CM|>r
(x0-a)2+(y0-b)2>r2
点M在圆内
|CM|
知识点拨
微练习
点P(1,3)与圆x2+y2=24的位置关系是( )
A.在圆外
B.在圆内
C.在圆上
D.不确定
答案:B
探究一
探究二
素养形成
当堂检测
求圆的标准方程
例1(1)圆心在点C(2,1),半径长是 的圆的标准方程为 .?
(2)圆心在点C(8,-3),且过点P(5,1)的圆的标准方程为 .?
(3)已知两点A(-1,-3),B(3,a),以线段AB为直径的圆经过原点,则该圆的标准方程为 .?
探究一
探究二
素养形成
当堂检测
因为以线段AB为直径的圆经过原点,
故(0,0)代入①成立,解得a=-1.
故圆的标准方程为(x-1)2+(y+2)2=5.
答案:(1)(x-2)2+(y-1)2=3
(2)(x-8)2+(y+3)2=25
(3)(x-1)2+(y+2)2=5
探究一
探究二
素养形成
当堂检测
反思感悟 1.确定圆的标准方程只需确定圆心坐标和半径,因此用直接法求圆的标准方程时,要首先求出圆心坐标和半径,然后直接写出圆的标准方程.
2.确定圆心和半径时,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”,“两条弦的中垂线的交点必为圆心”等.
探究一
探究二
素养形成
当堂检测
变式训练(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x+1)2+(y+2)2=100
B.(x-1)2+(y-2)2=100
C.(x+1)2+(y+2)2=25
D.(x-1)2+(y-2)2=25
(2)与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程为 .?
探究一
探究二
素养形成
当堂检测
解析:(1)∵AB为直径,∴AB的中点(1,2)为圆心,
∴该圆的标准方程为(x-1)2+(y-2)2=25.
(2)∵圆心坐标为(-5,-3),又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为(x+5)2+(y+3)2=25.
答案:(1)D (2)(x+5)2+(y+3)2=25
探究一
探究二
素养形成
当堂检测
点与圆的位置关系
例2已知在平面直角坐标系中有A(0,1),B(2,1),C(3,4),D(-1,2)四点,这四点能否在同一个圆上,为什么?
分析先确定出过其中三点的一个圆的方程,再验证第四个点是否在这个圆上,即可得出答案.
所以,经过A,B,C三点的圆的标准方程是(x-1)2+(y-3)2=5.
把点D的坐标(-1,2)代入上述圆的方程,得(-1-1)2+(2-3)2=5.
所以,点D在经过A,B,C三点的圆上,即A,B,C,D四点能在同一个圆上.
探究一
探究二
素养形成
当堂检测
反思感悟 判断点P(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系有几何法和代数法两种:
(1)对于几何法,主要是利用点与圆心的距离与半径比较大小;
(2)对于代数法,主要把点的坐标代入圆的标准方程,左端与r2比较.
延伸探究 试求过三点A(0,1),B(2,1),C(3,4)的圆的方程,并且判断点(3,6)与所求圆的关系.
解:所求方程同例题中的结论(x-1)2+(y-3)2=5.
经判断,因为点(3,6)代入圆方程左边可得(3-1)2+(6-3)2=13>5,因此点(3,6)在该圆外.
探究一
探究二
素养形成
当堂检测
一题多解——待定系数法与几何法求圆的标准方程
案例 求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
归纳提升(1)待定系数法求圆的标准方程的一般步骤
(2)几何法即是利用平面几何知识,求出圆心和半径,然后写出圆的标准方程.
(3)有时待定系数法和几何法交叉使用,体现数形结合的数学思想.
探究一
探究二
素养形成
当堂检测
1.圆心为(3,1),半径为5的圆的标准方程是( )
A.(x+3)2+(y+1)2=5 B.(x+3)2+(y+1)2=25
C.(x-3)2+(y-1)2=5 D.(x-3)2+(y-1)2=25
答案:D
2.若点(5a+1,12a)在圆(x-1)2+y2=1的内部,则实数a满足( )
答案:D
探究一
探究二
素养形成
当堂检测
3.圆心在y轴上,半径为1,且过点(1,2)的圆的标准方程是( )
A.x2+(y-2)2=1 B.x2+(y+2)2=1
C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1
解析:方法一:直接法
∴b=2,
∴圆的标准方程是x2+(y-2)2=1.
方法二:数形结合法
作图(如图),根据点(1,2)到圆心的距离为1易知,
圆心为(0,2),故圆的标准方程是x2+(y-2)2=1.
答案:A
探究一
探究二
素养形成
当堂检测
4.圆(x-3)2+(y+1)2=1关于直线x+y-3=0对称的圆的标准方程是 .?
解析:设圆心A(3,-1)关于直线x+y-3=0对称的点B的坐标为(a,b),
故所求圆的标准方程为(x-4)2+y2=1.
答案:(x-4)2+y2=1
探究一
探究二
素养形成
当堂检测
5.求过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的标准方程.
解:设圆的标准方程为(x-a)2+(y-b)2=r2,
根据已知条件可得
所以所求圆的标准方程为(x-1)2+(y-1)2=4.
