人教B版(2019)高中数学选择性必修第一册 2.3.4 圆与圆的位置关系(共29张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 2.3.4 圆与圆的位置关系(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览








文档简介
2.3.4 圆与圆的位置关系
核心素养
1.理解圆与圆的位置关系的种类.(数学抽象)
2.掌握圆与圆的位置关系的代数判断方法与几何判断方法.(逻辑推理)
3.能够利用上述方法判断两圆的位置关系.(逻辑推理)
4.体会根据圆的对称性灵活处理问题的方法和它的优越性.(直观想象)
思维脉络
激趣诱思
知识点拨
魔术钢圈有很多的版本,通常有三连环和四连环.三连环中,有一个环是有缺口的,而另外两个环是密封的;而四连环的原理基本相同,唯一不同的是有两个环本来
就连在一起,其余是一个有缺口的环和一个密封的环.表演时基本的手法是敲击法和摩擦法.敲击法:一手拿一个环,右手拿的是有缺口的环.缺口环的口要在右手的尾指处.用右手的环敲击左手的环.先装作敲两下,第三下时右手的环迅速向下敲,同时让左手的环的上端穿过右手的环的缺口,穿进去后便连在一起.摩擦法:同样一手拿一个环,其中一个当然是缺口环,不过你哪一只手拿缺口环都行.把两个环靠在一起,让两个环的一端进行摩擦.当然,缺口不能让别人看到,要用食指捂住.当两个环摩擦时,趁机让普通环的一端直接滑入缺口环的缺口处.成功滑入后,再摩擦两下,拉直两个环就行啦.
激趣诱思
知识点拨
在魔术师美轮美奂的表演中,对于圈而言,有时分开,有时相连;如果把魔术圈看成圆,那么图中两个圆的位置关系能否用圆心和半径来刻画呢?
激趣诱思
知识点拨
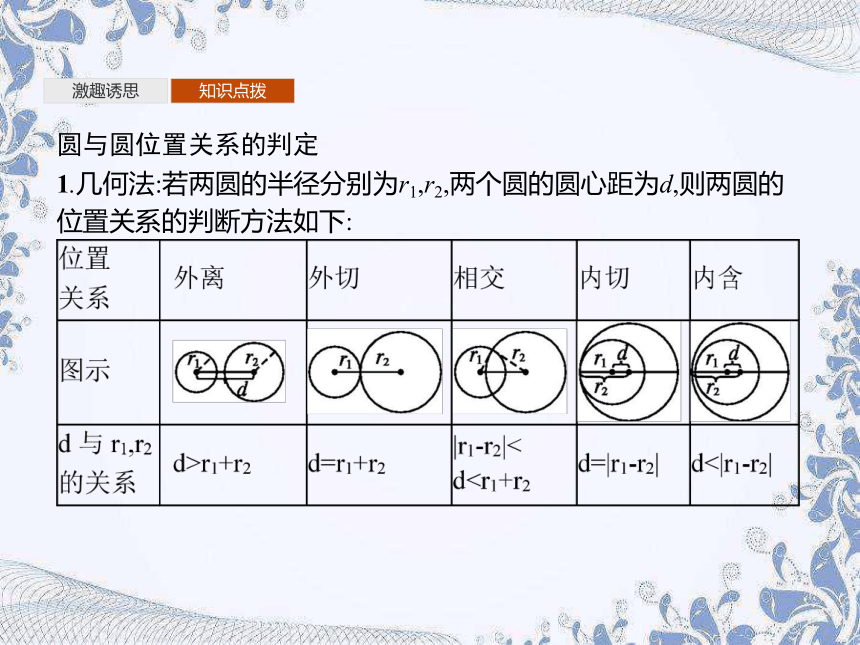
圆与圆位置关系的判定
1.几何法:若两圆的半径分别为r1,r2,两个圆的圆心距为d,则两圆的位置关系的判断方法如下:
激趣诱思
知识点拨
微判断
(1)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )
(2)若两圆有公共点,则|r1-r2|≤d≤r1+r2.( )
答案:(1)× (2)√
微思考
当两圆外离、外切、相交、内切、内含时,两圆的公切线分别有几条?
提示:两圆外离时,公切线有4条,外切时有3条,相交时有2条,内切时有1条,内含时没有公切线.
激趣诱思
知识点拨
方程组解的个数
2
1
0
两圆的公共点的个数
2
1
0
两圆的位置关系
相交
外切或内切
外离或内含
激趣诱思
知识点拨
微判断
如果两个圆的方程组成的方程组只有一组实数解,则两圆外切. ( )
答案:×
微思考
如果两圆相交,如何得到这两圆的公共弦所在的直线方程?
提示:当两圆相交时,可解两圆的方程所组成的方程组,得到两交点坐标,利用两点式得到两圆的公共弦所在的直线方程,也可以把两圆的方程作差消去x2和y2,就得到两圆的公共弦所在的直线方程.
探究一
探究二
探究三
素养形成
当堂检测
两圆位置关系的判断
例1(1)圆O1:x2+y2-2x=0与圆O2:x2+y2-2y=0的位置关系是( )
A.外离 B.相交 C.外切 D.内切
(2)圆O1:(x+2)2+(y-2)2=1与圆O2:(x-2)2+(y-5)2=16的位置关系为 .?
答案:(1)B (2)外切
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 判断两圆的位置关系常用两种方法
几何法和代数法,但一般情况下用几何法,即用两圆半径和圆心距之间的关系来刻画,此种方法形象直观,关键是明确圆心和半径,再套用圆与圆位置关系的关系式进行求解或判断.
延伸探究 若本例(1)中条件不变,所求改为“求圆O1与圆O2的公切线条数”结论又如何?
解:根据例题中结论☉O1与☉O2相交,则由平面几何知识可知,公切线条数为2.
探究一
探究二
探究三
素养形成
当堂检测
变式训练1已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,当m为何值时,分别满足下列情况:
(1)圆C1与圆C2外切;(2)圆C1与圆C2内含.
解:易得圆C1:(x-m)2+(y+2)2=9,圆心C1(m,-2),半径r1=3;
圆C2:(x+1)2+(y-m)2=4,圆心C2(-1,m),半径r2=2.
(1)如果圆C1与圆C2外切,
探究一
探究二
探究三
素养形成
当堂检测
两圆的公共弦问题
例2已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.
(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程,若不相交,请说明理由;
(2)求公共弦的长度.
探究一
探究二
探究三
素养形成
当堂检测
解:(1)相交.
将两圆方程配方化为标准方程,则
C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
∴|r1-r2|<|C1C2| 将两圆方程相减,得公共弦所在的直线方程为x-2y+4=0.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.当两圆相交时,公共弦所在的直线方程的求法
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在的直线方程为(D1-D2)x+(E1-E2)y+F1-F2=0.
2.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2(1)若圆x2+y2-2x+F=0和圆x2+y2+2x+Ey-4=0的公共弦所在的直线方程是x-y+1=0,则( )
A.E=-4,F=8 B.E=4,F=-8
C.E=-4,F=-8 D.E=4,F=8
(2)两圆x2+y2-10x-10y=0,x2+y2+6x+2y-40=0的公共弦的长为( )
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
圆系方程的应用
例3(1)对于任意实数λ,曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0恒过定点 .?
解析:曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0可化为(x2+y2+6x-16)+λ(x2+y2-4x-6)=0,
∴x2+y2+6x-16=0且x2+y2-4x-6=0,
可得恒过定点(1,3)和(1,-3).
答案:(1,3)和(1,-3)
探究一
探究二
探究三
素养形成
当堂检测
(2)求过直线x+y+4=0与圆x2+y2+4x-2y-4=0的交点且与直线y=x相切的圆的方程.
反思感悟 1.当经过两圆的交点时,圆的方程可设为(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0,然后用待定系数法求出λ即可.
2.当给出的方程结构中参数比较分散时,要注意将含参数的合并在一起,进而讨论过定点或交点问题.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3求圆心在直线x-y-4=0上,且过圆x2+y2-4x-6=0和圆x2+y2-4y-6=0的交点的圆的方程.
解:方法一:设经过两圆交点的圆系方程为x2+y2-4x-6+λ(x2+y2-4y-6)=0(λ≠-1),
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
易错点——因方程丢解而致错
案例 已知集合A={(x,y)|x2+y2=4},B={(x,y)|(x-3)2+(y-4)2=a2},若A∩B中有且仅有一个元素,求a的值.
错解:由条件A∩B中有且仅有一个元素可知两圆相切,所以|O1O2|=5=a+2或5=a-2.所以a=3或a=7.
错因分析本题错解产生的根源是误认为参数a是正数了.
正解:由A∩B中有且仅有一个元素,可知两圆相切,
所以|O1O2|=5=|a|+2或5=||a|-2|,
解得a=±3或a=±7.
综上所述,a的值为±3或±7.
探究一
探究二
探究三
素养形成
当堂检测
防范措施在圆的标准方程(x-a)2+(y-b)2=r2中要明确各个参数的含义,尤其是r这个量,当r代表圆的半径时,理所当然r>0.但在一些情景下,圆的标准方程(x-a)2+(y-b)2=m2只要保证等式右边是正数即可.也就是只需m2>0即可,这样m≠0即可.
探究一
探究二
探究三
素养形成
当堂检测
1.圆(x-3)2+(y+2)2=1与圆x2+y2-14x-2y+14=0的位置关系是( )
A.外切 B.内切 C.相交 D.外离
解析:圆x2+y2-14x-2y+14=0变形为(x-7)2+(y-1)2=36,圆心坐标为(7,1),半径为r1=6,圆(x-3)2+(y+2)2=1的圆心坐标为(3,-2),半径为
答案:B
探究一
探究二
探究三
素养形成
当堂检测
2.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程是( )
A.x+y+3=0 B.2x-y-5=0
C.3x-y-9=0 D.4x-3y+7=0
解析:AB的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A,B,D.
答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.若圆C1:(x+2)2+(y-m)2=9与圆C2:(x-m)2+(y+1)2=4外切,则m的值为 .?
解析:两圆的圆心坐标分别为(-2,m),(m,-1),
两圆的半径分别为3,2,
解得m=2或-5.
答案:2或-5
探究一
探究二
探究三
素养形成
当堂检测
4.圆C1:x2+y2-2x-8=0与圆C2:x2+y2+2x-4y-4=0的公共弦长为 .?
探究一
探究二
探究三
素养形成
当堂检测
5.已知圆C1:x2+y2+4x+1=0和圆C2:x2+y2+2x+2y+1=0,求以圆C1与圆C2的公共弦为直径的圆的方程.
核心素养
1.理解圆与圆的位置关系的种类.(数学抽象)
2.掌握圆与圆的位置关系的代数判断方法与几何判断方法.(逻辑推理)
3.能够利用上述方法判断两圆的位置关系.(逻辑推理)
4.体会根据圆的对称性灵活处理问题的方法和它的优越性.(直观想象)
思维脉络
激趣诱思
知识点拨
魔术钢圈有很多的版本,通常有三连环和四连环.三连环中,有一个环是有缺口的,而另外两个环是密封的;而四连环的原理基本相同,唯一不同的是有两个环本来
就连在一起,其余是一个有缺口的环和一个密封的环.表演时基本的手法是敲击法和摩擦法.敲击法:一手拿一个环,右手拿的是有缺口的环.缺口环的口要在右手的尾指处.用右手的环敲击左手的环.先装作敲两下,第三下时右手的环迅速向下敲,同时让左手的环的上端穿过右手的环的缺口,穿进去后便连在一起.摩擦法:同样一手拿一个环,其中一个当然是缺口环,不过你哪一只手拿缺口环都行.把两个环靠在一起,让两个环的一端进行摩擦.当然,缺口不能让别人看到,要用食指捂住.当两个环摩擦时,趁机让普通环的一端直接滑入缺口环的缺口处.成功滑入后,再摩擦两下,拉直两个环就行啦.
激趣诱思
知识点拨
在魔术师美轮美奂的表演中,对于圈而言,有时分开,有时相连;如果把魔术圈看成圆,那么图中两个圆的位置关系能否用圆心和半径来刻画呢?
激趣诱思
知识点拨
圆与圆位置关系的判定
1.几何法:若两圆的半径分别为r1,r2,两个圆的圆心距为d,则两圆的位置关系的判断方法如下:
激趣诱思
知识点拨
微判断
(1)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )
(2)若两圆有公共点,则|r1-r2|≤d≤r1+r2.( )
答案:(1)× (2)√
微思考
当两圆外离、外切、相交、内切、内含时,两圆的公切线分别有几条?
提示:两圆外离时,公切线有4条,外切时有3条,相交时有2条,内切时有1条,内含时没有公切线.
激趣诱思
知识点拨
方程组解的个数
2
1
0
两圆的公共点的个数
2
1
0
两圆的位置关系
相交
外切或内切
外离或内含
激趣诱思
知识点拨
微判断
如果两个圆的方程组成的方程组只有一组实数解,则两圆外切. ( )
答案:×
微思考
如果两圆相交,如何得到这两圆的公共弦所在的直线方程?
提示:当两圆相交时,可解两圆的方程所组成的方程组,得到两交点坐标,利用两点式得到两圆的公共弦所在的直线方程,也可以把两圆的方程作差消去x2和y2,就得到两圆的公共弦所在的直线方程.
探究一
探究二
探究三
素养形成
当堂检测
两圆位置关系的判断
例1(1)圆O1:x2+y2-2x=0与圆O2:x2+y2-2y=0的位置关系是( )
A.外离 B.相交 C.外切 D.内切
(2)圆O1:(x+2)2+(y-2)2=1与圆O2:(x-2)2+(y-5)2=16的位置关系为 .?
答案:(1)B (2)外切
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 判断两圆的位置关系常用两种方法
几何法和代数法,但一般情况下用几何法,即用两圆半径和圆心距之间的关系来刻画,此种方法形象直观,关键是明确圆心和半径,再套用圆与圆位置关系的关系式进行求解或判断.
延伸探究 若本例(1)中条件不变,所求改为“求圆O1与圆O2的公切线条数”结论又如何?
解:根据例题中结论☉O1与☉O2相交,则由平面几何知识可知,公切线条数为2.
探究一
探究二
探究三
素养形成
当堂检测
变式训练1已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,当m为何值时,分别满足下列情况:
(1)圆C1与圆C2外切;(2)圆C1与圆C2内含.
解:易得圆C1:(x-m)2+(y+2)2=9,圆心C1(m,-2),半径r1=3;
圆C2:(x+1)2+(y-m)2=4,圆心C2(-1,m),半径r2=2.
(1)如果圆C1与圆C2外切,
探究一
探究二
探究三
素养形成
当堂检测
两圆的公共弦问题
例2已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.
(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程,若不相交,请说明理由;
(2)求公共弦的长度.
探究一
探究二
探究三
素养形成
当堂检测
解:(1)相交.
将两圆方程配方化为标准方程,则
C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
∴|r1-r2|<|C1C2|
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.当两圆相交时,公共弦所在的直线方程的求法
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在的直线方程为(D1-D2)x+(E1-E2)y+F1-F2=0.
2.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2(1)若圆x2+y2-2x+F=0和圆x2+y2+2x+Ey-4=0的公共弦所在的直线方程是x-y+1=0,则( )
A.E=-4,F=8 B.E=4,F=-8
C.E=-4,F=-8 D.E=4,F=8
(2)两圆x2+y2-10x-10y=0,x2+y2+6x+2y-40=0的公共弦的长为( )
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
圆系方程的应用
例3(1)对于任意实数λ,曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0恒过定点 .?
解析:曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0可化为(x2+y2+6x-16)+λ(x2+y2-4x-6)=0,
∴x2+y2+6x-16=0且x2+y2-4x-6=0,
可得恒过定点(1,3)和(1,-3).
答案:(1,3)和(1,-3)
探究一
探究二
探究三
素养形成
当堂检测
(2)求过直线x+y+4=0与圆x2+y2+4x-2y-4=0的交点且与直线y=x相切的圆的方程.
反思感悟 1.当经过两圆的交点时,圆的方程可设为(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0,然后用待定系数法求出λ即可.
2.当给出的方程结构中参数比较分散时,要注意将含参数的合并在一起,进而讨论过定点或交点问题.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3求圆心在直线x-y-4=0上,且过圆x2+y2-4x-6=0和圆x2+y2-4y-6=0的交点的圆的方程.
解:方法一:设经过两圆交点的圆系方程为x2+y2-4x-6+λ(x2+y2-4y-6)=0(λ≠-1),
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
易错点——因方程丢解而致错
案例 已知集合A={(x,y)|x2+y2=4},B={(x,y)|(x-3)2+(y-4)2=a2},若A∩B中有且仅有一个元素,求a的值.
错解:由条件A∩B中有且仅有一个元素可知两圆相切,所以|O1O2|=5=a+2或5=a-2.所以a=3或a=7.
错因分析本题错解产生的根源是误认为参数a是正数了.
正解:由A∩B中有且仅有一个元素,可知两圆相切,
所以|O1O2|=5=|a|+2或5=||a|-2|,
解得a=±3或a=±7.
综上所述,a的值为±3或±7.
探究一
探究二
探究三
素养形成
当堂检测
防范措施在圆的标准方程(x-a)2+(y-b)2=r2中要明确各个参数的含义,尤其是r这个量,当r代表圆的半径时,理所当然r>0.但在一些情景下,圆的标准方程(x-a)2+(y-b)2=m2只要保证等式右边是正数即可.也就是只需m2>0即可,这样m≠0即可.
探究一
探究二
探究三
素养形成
当堂检测
1.圆(x-3)2+(y+2)2=1与圆x2+y2-14x-2y+14=0的位置关系是( )
A.外切 B.内切 C.相交 D.外离
解析:圆x2+y2-14x-2y+14=0变形为(x-7)2+(y-1)2=36,圆心坐标为(7,1),半径为r1=6,圆(x-3)2+(y+2)2=1的圆心坐标为(3,-2),半径为
答案:B
探究一
探究二
探究三
素养形成
当堂检测
2.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程是( )
A.x+y+3=0 B.2x-y-5=0
C.3x-y-9=0 D.4x-3y+7=0
解析:AB的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A,B,D.
答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.若圆C1:(x+2)2+(y-m)2=9与圆C2:(x-m)2+(y+1)2=4外切,则m的值为 .?
解析:两圆的圆心坐标分别为(-2,m),(m,-1),
两圆的半径分别为3,2,
解得m=2或-5.
答案:2或-5
探究一
探究二
探究三
素养形成
当堂检测
4.圆C1:x2+y2-2x-8=0与圆C2:x2+y2+2x-4y-4=0的公共弦长为 .?
探究一
探究二
探究三
素养形成
当堂检测
5.已知圆C1:x2+y2+4x+1=0和圆C2:x2+y2+2x+2y+1=0,求以圆C1与圆C2的公共弦为直径的圆的方程.
