人教B版(2019)高中数学选择性必修第一册 2.5.1 椭圆的标准方程(共35张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 2.5.1 椭圆的标准方程(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览









文档简介
2.5.1 椭圆的标准方程
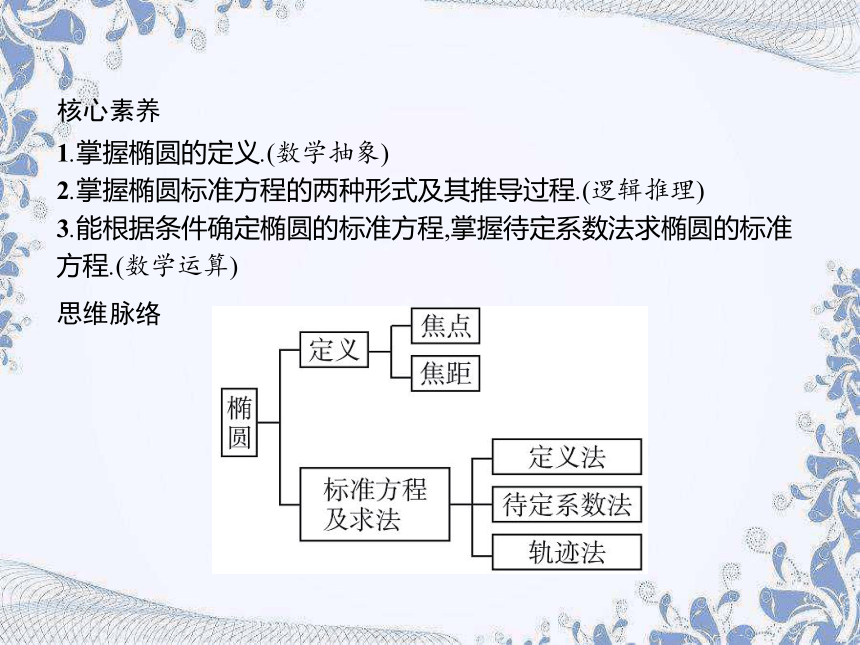
核心素养
1.掌握椭圆的定义.(数学抽象)
2.掌握椭圆标准方程的两种形式及其推导过程.(逻辑推理)
3.能根据条件确定椭圆的标准方程,掌握待定系数法求椭圆的标准方程.(数学运算)
思维脉络
激趣诱思
知识点拨
在2 000多年以前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果.其中数学家阿波罗尼奥斯采用平面截割圆锥的方法来研究这种曲线,他的著作《圆锥曲线论》是古代光辉的科学成果.下面探究几个最基础的问题:
激趣诱思
知识点拨
问题1 通过平面截割圆锥的方法你能得到几种曲线?
提示:用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,就能得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;继续用余下的倾斜角度的平面截割,可得到双曲线,见下图所示.
问题2 从集合或轨迹的角度,类比圆的定义,如何定义椭圆?
提示:平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
激趣诱思
知识点拨
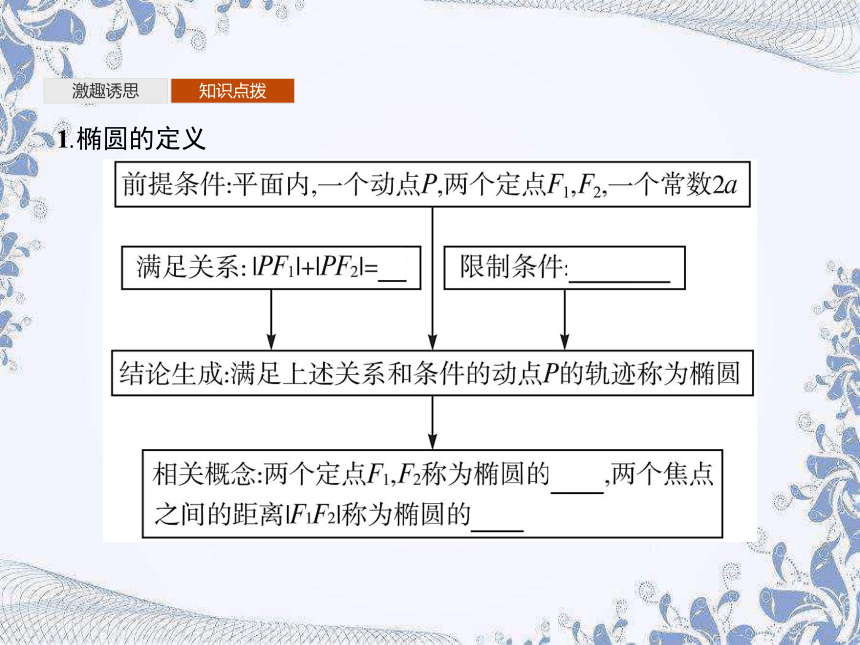
1.椭圆的定义
激趣诱思
知识点拨
微思考
椭圆的定义中去掉限制条件后,动点P的轨迹还是椭圆吗?
提示:不是.当2a<|F1F2|时,动点P的轨迹不存在.
当2a=|F1F2|时,动点P的轨迹为线段F1F2.
微练习
到两个定点F1(-7,0)和F2(7,0)的距离之和为14的点P的轨迹是( )
A.椭圆 B.线段
C.圆 D.以上都不对
解析:∵点P到两定点的距离之和为14等于|F1F2|,
∴轨迹是一条线段.
答案:B
激趣诱思
知识点拨
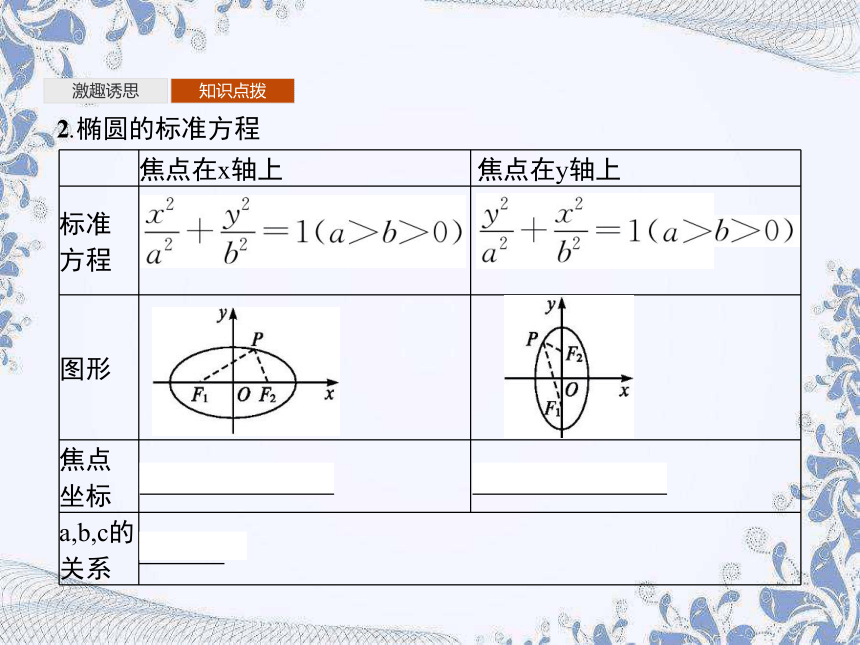
2.椭圆的标准方程
?
焦点在x轴上
焦点在y轴上
标准
方程
图形
焦点
坐标
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a,b,c的关系
b2=a2-c2
激趣诱思
知识点拨
名师点析 (1)在已知椭圆的标准方程解题时,应特别注意a>b>0这个条件.
(2)焦点三角形中常用的关系式
①|PF1|+|PF2|=2a.
激趣诱思
知识点拨
微练习
激趣诱思
知识点拨
解析:(2)设椭圆的左、右焦点分别为F1,F2,若|PF1|=2,
结合椭圆定义|PF2|+|PF1|=10,可得|PF2|=8.
答案:(1)D (2)D (3)C
激趣诱思
知识点拨
微思考
能否根据椭圆的标准方程,判定焦点位置?
提示:能.根据x2与y2的分母的大小来判定,哪个的分母大,焦点就在哪个轴上.
探究一
探究二
探究三
素养形成
当堂检测
待定系数法求椭圆的标准方程
例1求适合下列条件的椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
如果中心在原点,但焦点的位置不能明确是在x轴上,还是在y轴上,那么方程可以设为mx2+ny2=1(m>0,n>0,m≠n),进而求解.
2.待定系数法求圆锥曲线方程能有力地明晰数学运算的目标性和方向性,能较好地体现运用解析法进行数学运算的核心素养.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
定义法求椭圆的标准方程
例2求适合下列条件的椭圆的标准方程.
(1)焦点在y轴上,且经过两个点(0,2)和(1,0);
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 用定义法求椭圆的标准方程,先根据椭圆定义,确定a2,b2的值,再结合焦点位置写出椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2已知椭圆两个焦点的坐标分别是(0,5),(0,-5),椭圆上一点P到两焦点的距离之和为26,求满足条件的椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
椭圆定义的应用
例3如图所示,已知动圆P过定点A(-3,0),并且在定圆B:(x-3)2+y2=64的内部与其内切,求动圆圆心P的轨迹方程.
解:设动圆P和定圆B内切于点M,动圆圆心P到两定点A(-3,0)和B(3,0)的距离之和恰好等于定圆半径,
即|PA|+|PB|=|PM|+|PB|=|BM|=8>|AB|,
所以动圆圆心P的轨迹是以A,B为左、右焦点
的椭圆,其中c=3,a=4,b2=a2-c2=42-32=7,
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 利用椭圆定义求动点轨迹方程的三个步骤
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 (1)椭圆上一点P(不与焦点共线)与椭圆的两个焦点F1,F2构成的△PF1F2称为焦点三角形.解关于椭圆的焦点三角形的问题,通常要利用椭圆的定义,再结合正弦定理、余弦定理等知识求解.
(2)焦点三角形的常用公式
①焦点三角形的周长L=2a+2c.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究 若将例4中“ ∠F1PF2=60°”变为“∠PF1F2=90°”,求△F1PF2的面积.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
(3)由直线AB过椭圆的一个焦点F1,
知|AB|=|F1A|+|F1B|,
所以在△F2AB中,|F2A|+|F2B|+|AB|=4a=20,
又|F2A|+|F2B|=12,所以|AB|=8.
答案:(1)C (2)A (3)8
探究一
探究二
探究三
素养形成
当堂检测
易错点——因对椭圆的标准方程认识不清而致错
错因分析错解中没有注意到椭圆方程中a>b>0这一条件,当a=b时,方程并不表示椭圆.
探究一
探究二
探究三
素养形成
当堂检测
1.已知椭圆的焦点为(-1,0)和(1,0),点P(2,0)在椭圆上,则椭圆的方程为( )
答案:A
探究一
探究二
探究三
素养形成
当堂检测
2.若方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(0,+∞) B.(0,2)
C.(1,+∞) D.(0,1)
答案:D
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:4
探究一
探究二
探究三
素养形成
当堂检测
5.如图所示,在圆C:(x+1)2+y2=25内有一点A(1,0).Q为圆C上任意一点,线段AQ的垂直平分线与C,Q的连线交于点M,当点Q在圆C上运动时,求点M的轨迹方程.
探究一
探究二
探究三
素养形成
当堂检测
解:如图所示,连接MA.
由题意知点M在线段CQ上,
从而有|CQ|=|MQ|+|CM|.
又点M在AQ的垂直平分线上,
则|MA|=|MQ|,
故|MA|+|MC|=|CQ|=5>|AC|=2.
又A(1,0),C(-1,0),
故点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,
且2a=5,c=1,
核心素养
1.掌握椭圆的定义.(数学抽象)
2.掌握椭圆标准方程的两种形式及其推导过程.(逻辑推理)
3.能根据条件确定椭圆的标准方程,掌握待定系数法求椭圆的标准方程.(数学运算)
思维脉络
激趣诱思
知识点拨
在2 000多年以前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果.其中数学家阿波罗尼奥斯采用平面截割圆锥的方法来研究这种曲线,他的著作《圆锥曲线论》是古代光辉的科学成果.下面探究几个最基础的问题:
激趣诱思
知识点拨
问题1 通过平面截割圆锥的方法你能得到几种曲线?
提示:用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,就能得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;继续用余下的倾斜角度的平面截割,可得到双曲线,见下图所示.
问题2 从集合或轨迹的角度,类比圆的定义,如何定义椭圆?
提示:平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
激趣诱思
知识点拨
1.椭圆的定义
激趣诱思
知识点拨
微思考
椭圆的定义中去掉限制条件后,动点P的轨迹还是椭圆吗?
提示:不是.当2a<|F1F2|时,动点P的轨迹不存在.
当2a=|F1F2|时,动点P的轨迹为线段F1F2.
微练习
到两个定点F1(-7,0)和F2(7,0)的距离之和为14的点P的轨迹是( )
A.椭圆 B.线段
C.圆 D.以上都不对
解析:∵点P到两定点的距离之和为14等于|F1F2|,
∴轨迹是一条线段.
答案:B
激趣诱思
知识点拨
2.椭圆的标准方程
?
焦点在x轴上
焦点在y轴上
标准
方程
图形
焦点
坐标
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a,b,c的关系
b2=a2-c2
激趣诱思
知识点拨
名师点析 (1)在已知椭圆的标准方程解题时,应特别注意a>b>0这个条件.
(2)焦点三角形中常用的关系式
①|PF1|+|PF2|=2a.
激趣诱思
知识点拨
微练习
激趣诱思
知识点拨
解析:(2)设椭圆的左、右焦点分别为F1,F2,若|PF1|=2,
结合椭圆定义|PF2|+|PF1|=10,可得|PF2|=8.
答案:(1)D (2)D (3)C
激趣诱思
知识点拨
微思考
能否根据椭圆的标准方程,判定焦点位置?
提示:能.根据x2与y2的分母的大小来判定,哪个的分母大,焦点就在哪个轴上.
探究一
探究二
探究三
素养形成
当堂检测
待定系数法求椭圆的标准方程
例1求适合下列条件的椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
如果中心在原点,但焦点的位置不能明确是在x轴上,还是在y轴上,那么方程可以设为mx2+ny2=1(m>0,n>0,m≠n),进而求解.
2.待定系数法求圆锥曲线方程能有力地明晰数学运算的目标性和方向性,能较好地体现运用解析法进行数学运算的核心素养.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
定义法求椭圆的标准方程
例2求适合下列条件的椭圆的标准方程.
(1)焦点在y轴上,且经过两个点(0,2)和(1,0);
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 用定义法求椭圆的标准方程,先根据椭圆定义,确定a2,b2的值,再结合焦点位置写出椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2已知椭圆两个焦点的坐标分别是(0,5),(0,-5),椭圆上一点P到两焦点的距离之和为26,求满足条件的椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
椭圆定义的应用
例3如图所示,已知动圆P过定点A(-3,0),并且在定圆B:(x-3)2+y2=64的内部与其内切,求动圆圆心P的轨迹方程.
解:设动圆P和定圆B内切于点M,动圆圆心P到两定点A(-3,0)和B(3,0)的距离之和恰好等于定圆半径,
即|PA|+|PB|=|PM|+|PB|=|BM|=8>|AB|,
所以动圆圆心P的轨迹是以A,B为左、右焦点
的椭圆,其中c=3,a=4,b2=a2-c2=42-32=7,
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 利用椭圆定义求动点轨迹方程的三个步骤
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 (1)椭圆上一点P(不与焦点共线)与椭圆的两个焦点F1,F2构成的△PF1F2称为焦点三角形.解关于椭圆的焦点三角形的问题,通常要利用椭圆的定义,再结合正弦定理、余弦定理等知识求解.
(2)焦点三角形的常用公式
①焦点三角形的周长L=2a+2c.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究 若将例4中“ ∠F1PF2=60°”变为“∠PF1F2=90°”,求△F1PF2的面积.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
(3)由直线AB过椭圆的一个焦点F1,
知|AB|=|F1A|+|F1B|,
所以在△F2AB中,|F2A|+|F2B|+|AB|=4a=20,
又|F2A|+|F2B|=12,所以|AB|=8.
答案:(1)C (2)A (3)8
探究一
探究二
探究三
素养形成
当堂检测
易错点——因对椭圆的标准方程认识不清而致错
错因分析错解中没有注意到椭圆方程中a>b>0这一条件,当a=b时,方程并不表示椭圆.
探究一
探究二
探究三
素养形成
当堂检测
1.已知椭圆的焦点为(-1,0)和(1,0),点P(2,0)在椭圆上,则椭圆的方程为( )
答案:A
探究一
探究二
探究三
素养形成
当堂检测
2.若方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(0,+∞) B.(0,2)
C.(1,+∞) D.(0,1)
答案:D
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:4
探究一
探究二
探究三
素养形成
当堂检测
5.如图所示,在圆C:(x+1)2+y2=25内有一点A(1,0).Q为圆C上任意一点,线段AQ的垂直平分线与C,Q的连线交于点M,当点Q在圆C上运动时,求点M的轨迹方程.
探究一
探究二
探究三
素养形成
当堂检测
解:如图所示,连接MA.
由题意知点M在线段CQ上,
从而有|CQ|=|MQ|+|CM|.
又点M在AQ的垂直平分线上,
则|MA|=|MQ|,
故|MA|+|MC|=|CQ|=5>|AC|=2.
又A(1,0),C(-1,0),
故点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,
且2a=5,c=1,
