人教B版(2019)高中数学选择性必修第一册 2.6.2 双曲线的几何性质(共52张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 2.6.2 双曲线的几何性质(共52张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览










文档简介
2.6.2 双曲线的几何性质
核心素养
1.掌握双曲线的简单几何性质.(直观想象)
2.理解双曲线离心率的定义、取值范围和渐近线方程.(逻辑推理)
3.通过具体实例初步了解直线与双曲线相交的相关问题.(数学运算)
思维脉络
激趣诱思
知识点拨
火电厂、核电站的循环水自然通风冷却塔是一种大型薄壳型构筑物.建在水源不十分充足的地区的电厂,为了节约用水,需建造一个循环冷却水系统,以使得冷却器中排出的热水在其中冷却后可重复使用.大型电厂采用的冷却构筑物多为双曲线型冷却塔.这样从结构上最稳定,强度高,能够获得更大的容积,气流顺畅,对流冷却效果好,造型美观.
激趣诱思
知识点拨
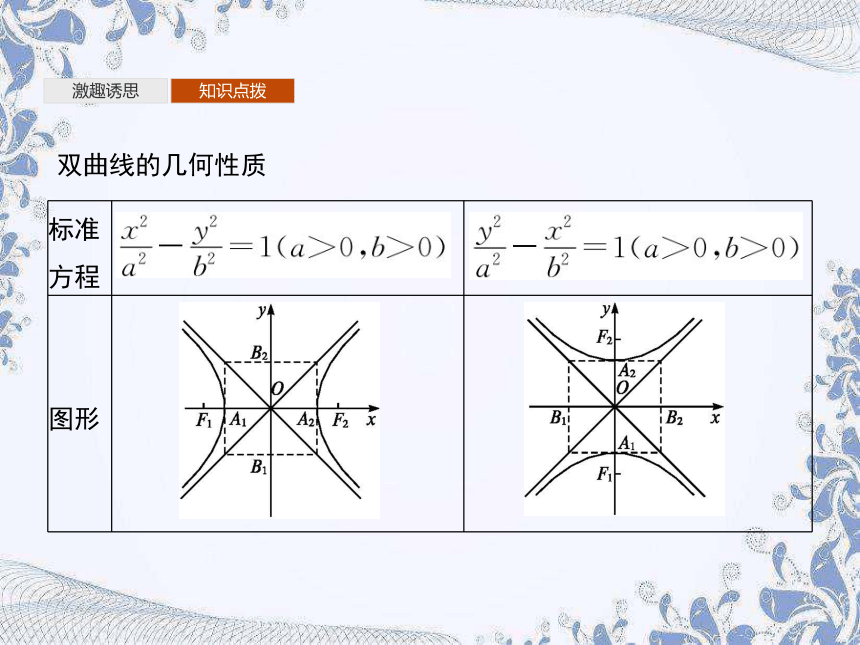
双曲线的几何性质
标准方程
图形
激趣诱思
知识点拨
标准方程
性
质
范围
x≤-a或x≥a y∈R
y≤-a或y≥a x∈R
对称性
对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
实轴:线段A1A2,长:2a;
虚轴:线段B1B2,长:2b;
半实轴长:a,半虚轴长:b
渐近线
y=± x
y=± x
离心率
a,b,c间的关系
c2=a2+b2(c>a>0,c>b>0)
名师点析 (1)双曲线与椭圆的六个不同点:
?
双曲线
椭圆
曲线
两支曲线
封闭的曲线
顶点
两个顶点
四个顶点
轴
实、虚轴
长、短轴
渐近线
有渐近线
无渐近线
离心率
e>1
0 a,b,c关系
a2+b2=c2
a2-b2=c2
(2)等轴双曲线是实轴和虚轴等长的双曲线,它的渐近线方程是y=±x,离心率为 .
(3)共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.
激趣诱思
知识点拨
激趣诱思
知识点拨
微练习
A.-5 B.-35
C.19 D.-11
答案:B
激趣诱思
知识点拨
答案:A
激趣诱思
知识点拨
微判断
答案:(1)√ (2)× (3)√
激趣诱思
知识点拨
微思考
(1)双曲线的离心率对开口大小有怎样的影响?
提示:双曲线的离心率e= 反映了双曲线开口的大小,e越大,双曲线的开口就越大.
(2)一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点?
提示:1个.
探究一
探究二
探究三
素养形成
当堂检测
由双曲线方程研究其几何性质
例1求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 由双曲线的方程研究其几何性质的注意点
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究 求双曲线nx2-my2=mn(m>0,n>0)的半实轴长、半虚轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
探究一
探究二
探究三
素养形成
当堂检测
例2已知F1,F2为双曲线 (a>0,b>0)的左、右焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°,求该双曲线的渐近线方程.
分析求双曲线的渐近线方程就必须求渐近线的斜率,也就是求a,b间的关系.本题利用双曲线的定义和直角三角形边、角之间的关系,求a,b间的关系.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.根据双曲线的标准方程求它的渐近线方程的方法中,最简单且实用的是把双曲线标准方程中等号右边的“1”改成“0”,就得到了此双曲线的渐近线方程.
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
由双曲线的几何性质求标准方程
例3根据以下条件,求双曲线的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.根据双曲线的某些几何性质求双曲线的标准方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
探究一
探究二
探究三
素养形成
当堂检测
2.巧设双曲线方程的六种方法与技巧
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
探究一
探究二
探究三
素养形成
当堂检测
变式训练2求适合下列条件的双曲线的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
直线与双曲线的位置关系
例4(1)已知平面上两点M(-5,0)和N(5,0),若直线上存在点P使|PM|-|PN|=6,则称该直线为“单曲型直线”,下列直线中:
①y=x+1;②y=2;③y= x;④y=2x+1.
其中是“单曲型直线”的是 .?
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:①②
探究一
探究二
探究三
素养形成
当堂检测
(2)已知双曲线焦距为4,焦点在x轴上,且过点P(2,3).
①求该双曲线的标准方程;
②若直线m经过该双曲线的右焦点且斜率为1,求直线m被双曲线截得的弦长.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.直线与双曲线位置关系的判定方法
通常把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考查方程的判别式.
(1)Δ>0时,直线与双曲线有两个不同的公共点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ<0时,直线与双曲线没有公共点.
当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点.
探究一
探究二
探究三
素养形成
当堂检测
2.双曲线的弦长公式
和直线与椭圆相交所得的弦的长度求法一样.设直线y=kx+b与双
3.如果利用“点差法”解题,其过程是无法保证直线与双曲线相交的,因此必须对所得直线方程的存在性进行验证.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3(1)已知双曲线方程为x2- =1,过点P(1,0)的直线l与双曲线只有一个公共点,则l共有 ( )
A.4条 B.3条 C.2条 D.1条
解析:因为双曲线方程为x2- =1,则P(1,0)是双曲线的右顶点,所以过P(1,0)并且和x轴垂直的直线是双曲线的一条切线,与双曲线只有一个公共点,另外两条就是过P(1,0)分别和两条渐近线平行的直线,所以符合要求的有3条.
答案:B
探究一
探究二
探究三
素养形成
当堂检测
(2)已知双曲线2x2-y2=2,过点B(1,1)能否作直线l,使l与所给双曲线交于点Q1,Q2,且B是弦Q1Q2的中点,若存在这样的直线l,求出它的方程;若不存在,请说明理由.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
(3)已知双曲线C:x2-y2=1及直线l:y=kx-1.
①若直线l与双曲线C有两个不同的交点,求实数k的取值范围;
②若直线l与双曲线C交于A,B两点,O是坐标原点,且△AOB的面积为 ,求实数k的值.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
专项探究 离心率问题
答案:A
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
归纳总结求双曲线的离心率
(1)求双曲线的离心率或其范围的方法
②列出含有a,b,c的齐次方程或不等式,借助于b2=c2-a2消去b,然后转化成关于e的方程或不等式求解.
(2)求解时,若用到特殊几何图形,可运用几何性质使问题简化.
探究一
探究二
探究三
素养形成
当堂检测
迁移应用1(2019浙江,2)渐近线方程为x±y=0的双曲线的离心率是( )
答案:C
探究一
探究二
探究三
素养形成
当堂检测
答案:D
探究一
探究二
探究三
素养形成
当堂检测
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )
答案:C
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:AD
探究一
探究二
探究三
素养形成
当堂检测
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲线的方程是 .?
解析:令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
答案:x2-y2=8
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:②④⑤
探究一
探究二
探究三
素养形成
当堂检测
|PF|-|AP|=2a=4,①
|QF|-|QA|=2a=4,②
①+②得|PF|+|QF|-|PQ|=8,
∴周长为|PF|+|QF|+|PQ|=8+2|PQ|=32.
答案:32
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
核心素养
1.掌握双曲线的简单几何性质.(直观想象)
2.理解双曲线离心率的定义、取值范围和渐近线方程.(逻辑推理)
3.通过具体实例初步了解直线与双曲线相交的相关问题.(数学运算)
思维脉络
激趣诱思
知识点拨
火电厂、核电站的循环水自然通风冷却塔是一种大型薄壳型构筑物.建在水源不十分充足的地区的电厂,为了节约用水,需建造一个循环冷却水系统,以使得冷却器中排出的热水在其中冷却后可重复使用.大型电厂采用的冷却构筑物多为双曲线型冷却塔.这样从结构上最稳定,强度高,能够获得更大的容积,气流顺畅,对流冷却效果好,造型美观.
激趣诱思
知识点拨
双曲线的几何性质
标准方程
图形
激趣诱思
知识点拨
标准方程
性
质
范围
x≤-a或x≥a y∈R
y≤-a或y≥a x∈R
对称性
对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
实轴:线段A1A2,长:2a;
虚轴:线段B1B2,长:2b;
半实轴长:a,半虚轴长:b
渐近线
y=± x
y=± x
离心率
a,b,c间的关系
c2=a2+b2(c>a>0,c>b>0)
名师点析 (1)双曲线与椭圆的六个不同点:
?
双曲线
椭圆
曲线
两支曲线
封闭的曲线
顶点
两个顶点
四个顶点
轴
实、虚轴
长、短轴
渐近线
有渐近线
无渐近线
离心率
e>1
0
a2+b2=c2
a2-b2=c2
(2)等轴双曲线是实轴和虚轴等长的双曲线,它的渐近线方程是y=±x,离心率为 .
(3)共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.
激趣诱思
知识点拨
激趣诱思
知识点拨
微练习
A.-5 B.-35
C.19 D.-11
答案:B
激趣诱思
知识点拨
答案:A
激趣诱思
知识点拨
微判断
答案:(1)√ (2)× (3)√
激趣诱思
知识点拨
微思考
(1)双曲线的离心率对开口大小有怎样的影响?
提示:双曲线的离心率e= 反映了双曲线开口的大小,e越大,双曲线的开口就越大.
(2)一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点?
提示:1个.
探究一
探究二
探究三
素养形成
当堂检测
由双曲线方程研究其几何性质
例1求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 由双曲线的方程研究其几何性质的注意点
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究 求双曲线nx2-my2=mn(m>0,n>0)的半实轴长、半虚轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
探究一
探究二
探究三
素养形成
当堂检测
例2已知F1,F2为双曲线 (a>0,b>0)的左、右焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°,求该双曲线的渐近线方程.
分析求双曲线的渐近线方程就必须求渐近线的斜率,也就是求a,b间的关系.本题利用双曲线的定义和直角三角形边、角之间的关系,求a,b间的关系.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.根据双曲线的标准方程求它的渐近线方程的方法中,最简单且实用的是把双曲线标准方程中等号右边的“1”改成“0”,就得到了此双曲线的渐近线方程.
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
由双曲线的几何性质求标准方程
例3根据以下条件,求双曲线的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.根据双曲线的某些几何性质求双曲线的标准方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
探究一
探究二
探究三
素养形成
当堂检测
2.巧设双曲线方程的六种方法与技巧
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
探究一
探究二
探究三
素养形成
当堂检测
变式训练2求适合下列条件的双曲线的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
直线与双曲线的位置关系
例4(1)已知平面上两点M(-5,0)和N(5,0),若直线上存在点P使|PM|-|PN|=6,则称该直线为“单曲型直线”,下列直线中:
①y=x+1;②y=2;③y= x;④y=2x+1.
其中是“单曲型直线”的是 .?
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:①②
探究一
探究二
探究三
素养形成
当堂检测
(2)已知双曲线焦距为4,焦点在x轴上,且过点P(2,3).
①求该双曲线的标准方程;
②若直线m经过该双曲线的右焦点且斜率为1,求直线m被双曲线截得的弦长.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.直线与双曲线位置关系的判定方法
通常把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考查方程的判别式.
(1)Δ>0时,直线与双曲线有两个不同的公共点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ<0时,直线与双曲线没有公共点.
当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点.
探究一
探究二
探究三
素养形成
当堂检测
2.双曲线的弦长公式
和直线与椭圆相交所得的弦的长度求法一样.设直线y=kx+b与双
3.如果利用“点差法”解题,其过程是无法保证直线与双曲线相交的,因此必须对所得直线方程的存在性进行验证.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3(1)已知双曲线方程为x2- =1,过点P(1,0)的直线l与双曲线只有一个公共点,则l共有 ( )
A.4条 B.3条 C.2条 D.1条
解析:因为双曲线方程为x2- =1,则P(1,0)是双曲线的右顶点,所以过P(1,0)并且和x轴垂直的直线是双曲线的一条切线,与双曲线只有一个公共点,另外两条就是过P(1,0)分别和两条渐近线平行的直线,所以符合要求的有3条.
答案:B
探究一
探究二
探究三
素养形成
当堂检测
(2)已知双曲线2x2-y2=2,过点B(1,1)能否作直线l,使l与所给双曲线交于点Q1,Q2,且B是弦Q1Q2的中点,若存在这样的直线l,求出它的方程;若不存在,请说明理由.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
(3)已知双曲线C:x2-y2=1及直线l:y=kx-1.
①若直线l与双曲线C有两个不同的交点,求实数k的取值范围;
②若直线l与双曲线C交于A,B两点,O是坐标原点,且△AOB的面积为 ,求实数k的值.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
专项探究 离心率问题
答案:A
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
归纳总结求双曲线的离心率
(1)求双曲线的离心率或其范围的方法
②列出含有a,b,c的齐次方程或不等式,借助于b2=c2-a2消去b,然后转化成关于e的方程或不等式求解.
(2)求解时,若用到特殊几何图形,可运用几何性质使问题简化.
探究一
探究二
探究三
素养形成
当堂检测
迁移应用1(2019浙江,2)渐近线方程为x±y=0的双曲线的离心率是( )
答案:C
探究一
探究二
探究三
素养形成
当堂检测
答案:D
探究一
探究二
探究三
素养形成
当堂检测
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )
答案:C
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:AD
探究一
探究二
探究三
素养形成
当堂检测
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲线的方程是 .?
解析:令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
答案:x2-y2=8
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
答案:②④⑤
探究一
探究二
探究三
素养形成
当堂检测
|PF|-|AP|=2a=4,①
|QF|-|QA|=2a=4,②
①+②得|PF|+|QF|-|PQ|=8,
∴周长为|PF|+|QF|+|PQ|=8+2|PQ|=32.
答案:32
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
