人教B版(2019)高中数学选择性必修第一册 1.2.2 空间中的平面与空间向量(共56张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 1.2.2 空间中的平面与空间向量(共56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览











文档简介
1.2.2 空间中的平面与空间向量
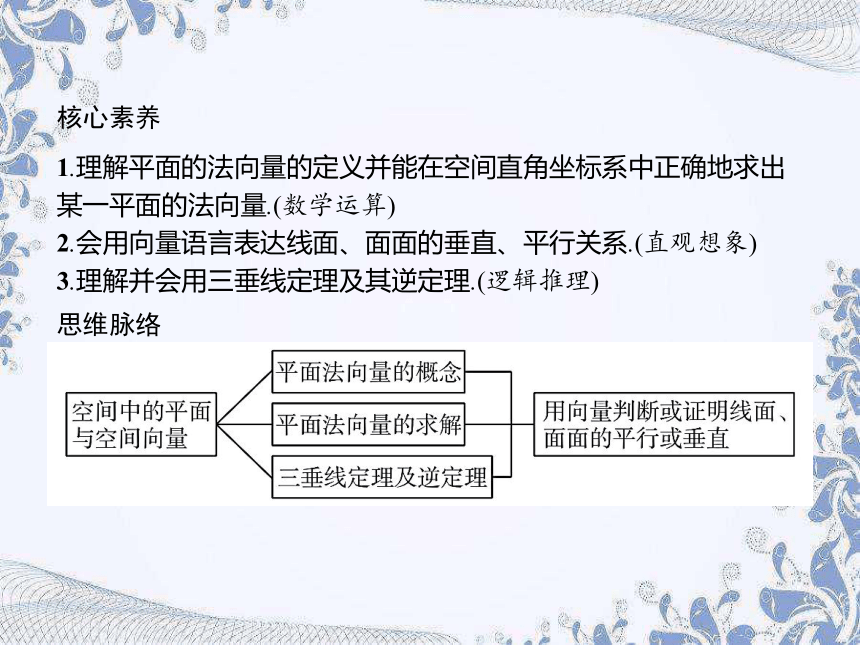
核心素养
1.理解平面的法向量的定义并能在空间直角坐标系中正确地求出某一平面的法向量.(数学运算)
2.会用向量语言表达线面、面面的垂直、平行关系.(直观想象)
3.理解并会用三垂线定理及其逆定理.(逻辑推理)
思维脉络
激趣诱思
知识点拨
牌楼,与牌坊类似,是中国传统建筑之一,最早见于周朝.在园林、寺观、宫苑、陵墓和街道常有建造.旧时牌楼主要有木、石、木石、砖木、琉璃等几种,多设于要道口.牌楼中有一种柱门形结构,一般较高大.如图,牌楼的柱子与地面是垂直的,如果牌楼上部的下边线与柱子垂直,我们就能知道下边线与地面平行.这是为什么呢?
激趣诱思
知识点拨
1.平面的法向量
如果α是空间中的一个平面,n是空间中的一个非零向量,且表示n的有向线段所在的直线与平面α垂直,则称n为平面α的一个法向量.此时,也称n与平面α垂直,记作n⊥α.
微思考
一个平面的法向量是否唯一?
提示:不唯一,一个平面的法向量有无数多个.
激趣诱思
知识点拨
2.平面的法向量的求法
在空间直角坐标系下,求平面的法向量的一般步骤:
(1)设平面的法向量为n=(x,y,z);
(2)找出(求出)平面内的两个不共线的向量a=(a1,b1,c1),b=(a2,b2,c2);
(4)解方程组,取其中的一组解,即得平面的一个法向量.
激趣诱思
知识点拨
微练习
点A(a,0,0),B(0,b,0),C(0,0,c),则平面ABC的一个法向量为( )
A.(bc,ac,ab) B.(ac,ab,bc)
C.(bc,ab,ac) D.(ab,ac,bc)
答案:A
激趣诱思
知识点拨
3.用空间向量处理平行或垂直关系
(1)如果v是直线l的一个方向向量,n是平面α的一个法向量,则n∥v?l⊥α;n⊥v?l∥α,或l?α.
(2)如果n1是平面α1的一个法向量,n2是平面α2的一个法向量,则
n1⊥n2?α1⊥α2;n1∥n2?α1∥α2,或α1与α2重合.
名师点析 解答这类问题的关键:一是要清楚直线的方向向量,平面的法向量和直线、平面的位置关系之间的内在联系;二是熟练掌握判断向量共线、垂直的方法.在把向量问题转化为几何问题时,要注意两者的区别,直线的方向向量和平面平行,则直线可能在平面内,也可能与平面平行.
激趣诱思
知识点拨
微练习
设直线l的一个方向向量d=(6,2,3),平面α的一个法向量n=(-1,3,0),则直线l与平面α的位置关系是( )
A.垂直 B.平行
C.直线l在平面α内 D.直线l在平面α内或平行
答案:D
激趣诱思
知识点拨
微判断
(1)若平面外的一条直线的方向向量与平面的法向量垂直,则该直线与平面平行.( )
(2)直线的方向向量与平面的法向量的方向相同或相反时,直线与平面垂直.( )
(3)两个平面的法向量平行,则这两个平面平行或重合;两个平面的法向量垂直,则这两个平面垂直.( )
答案:(1)√ (2)√ (3)√
激趣诱思
知识点拨
4.三垂线定理及三垂线定理的逆定理
三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直.
三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直.
微思考
三垂线定理及其逆定理有何区别与联系?
提示:联系:都是一面四线,三种垂直关系.
区别:①从条件或结论上看,三垂线定理是“线与射影垂直?线与斜线垂直”,而逆定理恰好相反;②从作用上看,三垂线定理是“共面直线垂直?异面直线垂直”,而逆定理恰好相反.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
求平面的法向量
例1
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.AB=AP=1,AD= ,试建立恰当的空间直角坐标系,求平面ACE的一个法向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 通过此类例题的解答,在求平面的法向量时要注意:
(1)选向量:在选取平面内的向量时,要选取不共线的两个向量.
(2)取特值:在求n的坐标时,可令x,y,z中一个为特殊值得另两个值,得到平面的一个法向量.
(3)注意0:提前假定法向量n=(x,y,z)的某个坐标为某特定值时一定要注意这个坐标不为0.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
延伸探究 本例条件不变,试求直线PC的一个方向向量和平面PCD的一个法向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练1已知△ABC的三个顶点的坐标分别为A(2,1,0),B(0,2,3),C(1,1,3),试求出平面ABC的一个法向量.
解:设平面ABC的法向量为n=(x,y,z).
∵A(2,1,0),B(0,2,3),C(1,1,3),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
利用空间向量证明平行问题
例2已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:(1)建立如图所示的空间直角坐标系Dxyz,
则D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 证明线面、面面平行问题的方法
(1)用向量法证明线面平行:①证明直线的方向向量与平面内的某一向量是共线向量且直线不在平面内;②证明直线的方向向量可以用平面内两个不共线向量表示且直线不在平面内;③证明直线的方向向量与平面的法向量垂直且直线不在平面内,如(1)中,FC1?平面ADE一定不能漏掉.
(2)利用空间向量证明面面平行,通常是证明两平面的法向量平行.当然要注意当法向量坐标中有0时,要使用n1=λn2这一形式.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练2
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC= AD=1,问在棱PD上是否存在一点E,使CE∥平面PAB?若存在,求出E点的位置;若不存在,请说明理由.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
解:存在点E使CE∥平面PAB.
以A为坐标原点,分别以AB,AD,AP所在直线为x轴,y轴,z轴建立空间直角坐标系Axyz,
∴P(0,0,1),C(1,1,0),D(0,2,0),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明线面垂直问题
例3如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:如图所示,取BC的中点O,连接AO.
因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,且平面ABC∩平面BCC1B1=BC,AO?平面ABC,所以AO⊥平面BCC1B1.
取B1C1的中点O1,以O为坐标原点,OB,OO1,OA所在直线分别为x轴,y轴,z轴,建立空间直角坐标系Oxyz,
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 1.用坐标法证明线面垂直的常用方法:
方法一:基向量法
(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)找出平面内两条相交直线,并用坐标表示它们的方向向量.
(4)分别计算两组向量的数量积,得到数量积为0.
方法二:坐标法
(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)求出平面的法向量.
(4)判断直线的方向向量与平面的法向量平行.
2.对于容易建系的几何载体要尽量用坐标法处理有关垂直问题,如果只用基向量法解决涉及的线性运算和数量积运算比较复杂.而建系后只需一切交给坐标即可.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
延伸探究 本例中增加条件,E,F分别是BC,BB1的中点,求证:EF⊥平面ADE.
即EF⊥EA,EF⊥ED,
又EA∩ED=E,EA,ED?平面ADE,
∴EF⊥平面ADE.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练3如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:方法一 设正方体的棱长为2,建立如图所示的空间直角坐标系,
则A(2,0,0),C(0,2,0),B1(2,2,2),E(2,2,1),F(1,1,2).
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明面面垂直问题
例4
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,
求证:平面ADE⊥平面ABE.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:取BE的中点O,连接OC,又AB⊥平面BCE,所以以O为原点建立空间直角坐标系Oxyz(如图所示).
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
又AB⊥平面BCE,OC?平面BCE,
所以AB⊥OC.
因为BE⊥OC,AB∩BE=B,AB,BE?平面ABE,
所以OC⊥平面ABE.
反思感悟 证明面面垂直的两种方法
(1)常规法:利用面面垂直的判定定理转化为线面垂直、线线垂直去证明.
(2)向量法:证明两个平面的法向量互相垂直.此例就是用的向量法,关键是明确两个平面的法向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练4在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在直线AE上求一点M,使得A1M⊥平面AED.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
(1)证明:以D为坐标原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系Dxyz.
设正方体的棱长为2,则D(0,0,0),A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2),D1(0,0,2),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
三垂线定理及其逆定理
例5如图,空间四边形ABCD中,点A在平面BCD内的射影 O1是△BCD的垂心,求证:B在平面ACD内的射影O2必是△ACD的垂心.
分析应用三垂线定理一定要分清斜线与射影,并注意第三条垂线要与射影在同一平面内.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:连接DO1,BO1,AO2,CO2.
∵O1是△BCD的垂心,∴DO1⊥BC.
又AO1⊥平面BCD,∴BC⊥AD(三垂线定理).
∵BC是平面ACD的斜线,BO2⊥平面ACD,CO2是BC在平面ACD内的射影,
∴CO2⊥AD(三垂线定理的逆定理).
同理,AO2⊥CD.
∴O2是△ACD的垂心.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 1.三垂线定理及其逆定理常用于判定空间直线互相垂直,在引用时要清楚以下问题:
(1)从条件上看,三垂线定理的条件是“和射影垂直”;其逆定理的条件是“和斜线垂直”.显然本例中三垂线定理和三垂线定理的逆定理都充分利用了.
(2)从功能上看,三垂线定理用于解决已知共面垂直,证明异面垂直的问题;逆定理正好相反.解决垂心问题需要两次垂直的证明,都能用上定理和其逆定理的框架结构.
2.三垂线定理及其逆定理应用中的三个环节
用三垂线定理及其逆定理证明线线垂直的关键在于构造三垂线定理的基本图形,创设应用定理的环境.构造三垂线定理基本图形时要抓住下面三个环节:(1)确定投影面;(2)作出垂线;(3)确定射影.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练5
如图,BC是Rt△ABC的斜边,过点A作△ABC所在平面α的垂线AP,连接PB,PC,过点A作AD⊥BC于点D,连接PD,那么图中的直角三角形共有( )
A.4个 B.6个 C.7个 D.8个
解析:∵AP⊥平面α,
∴PD在平面α内的射影为AD,
∵AD⊥BC,
由三垂线定理可得,PD⊥BC,
∴△ABC,△ABD,△ACD,△PBD,△PCD,△PAB,△PAD,△PAC均为直角三角形,共8个.
故选D.
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练6
如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上.
已知:∠BAC在平面α内,点P在α外,PE⊥AB,PF⊥AC,PO⊥α,垂足分别是E,F,O,PE=PF.
求证:∠BAO=∠CAO.
证明:连接PA,OE,OF.
∵PE⊥AB,PF⊥AC,PO⊥α,
∴AB⊥OE,AC⊥OF(三垂线定理的逆定理),
∵PE=PF,PA=PA,∴Rt△PAE≌Rt△PAF.
∴AE=AF.又AO=AO,∴Rt△AOE≌Rt△AOF.
∴∠BAO=∠CAO.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
平行或垂直证明中的探索类问题
一、平行证明中的探索类问题
案例 1如图所示,在正方体AC1中,O为底面ABCD中心,P是DD1的中点,设Q是CC1上的点,当点Q在什么位置时,平面D1BQ∥平面PAO.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
解:如图所示,分别以DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,在CC1上任取一点Q,连接BQ,D1Q.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
归纳提升(1)求点的坐标:可设出对应点的坐标,根据面面平行的判定定理转化为向量共线问题或者利用两个平面的法向量共线,进而建立与所求点的坐标有关的等式.
(2)由结论推应具备的条件的逆向推理是逻辑推理中的一种基本形式,通过应用推理的方式与方法,能较好地培养学生的合乎逻辑的思维品质.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
二、垂直证明中的探索类问题
案例 2在正方体ABCD-A1B1C1D1中,E是棱BC的中点,试在棱CC1上求一点P,使得平面A1B1P⊥平面C1DE.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
解:如图,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.设正方体的棱长为1,
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
归纳提升立体几何中探索性、存在性问题的思维层次较高,分析时应特别注意.本例由题意设出探求点的坐标,利用两平面垂直,法向量的位置关系及严密的逻辑推理,从而得出点P的坐标.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
1.若直线l的方向向量a=(1,0,2),平面α的法向量为n=(-2,0,-4),则( )
A.l∥α
B.l⊥α
C.l?α
D.l与α斜交
解析:∵n=-2a,∴a∥n,即l⊥α.
答案:B
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
3.若平面α,β的法向量分别为a=(2,-1,0),b=(-1,-2,0),则α与β的位置关系是( )
A.平行
B.垂直
C.相交但不垂直
D.无法确定
解析:a·b=-2+2+0=0,∴a⊥b,∴α⊥β.
答案:B
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
4.如图,在△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的度数( )
A.逐渐变大 B.逐渐变小
C.不变 D.先变大再变小
解析:由题意可得,AC⊥BC.
∵PA⊥平面ABC,
由三垂线定理的逆定理可得,BC⊥PC.
∴∠PCB=90°,
即∠PCB的度数保持不变.
故选C.
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:①②③
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
6.如图所示,在空间图形P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,CD∥AB,∠ABC=∠BCD=90°,AB=4,CD=1,点M在PB上,且PB=4PM,∠PBC=30°,求证:CM∥平面PAD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
7.在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°,E,F分别是AC,AD的中点,求证:平面BEF⊥平面ABC.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
核心素养
1.理解平面的法向量的定义并能在空间直角坐标系中正确地求出某一平面的法向量.(数学运算)
2.会用向量语言表达线面、面面的垂直、平行关系.(直观想象)
3.理解并会用三垂线定理及其逆定理.(逻辑推理)
思维脉络
激趣诱思
知识点拨
牌楼,与牌坊类似,是中国传统建筑之一,最早见于周朝.在园林、寺观、宫苑、陵墓和街道常有建造.旧时牌楼主要有木、石、木石、砖木、琉璃等几种,多设于要道口.牌楼中有一种柱门形结构,一般较高大.如图,牌楼的柱子与地面是垂直的,如果牌楼上部的下边线与柱子垂直,我们就能知道下边线与地面平行.这是为什么呢?
激趣诱思
知识点拨
1.平面的法向量
如果α是空间中的一个平面,n是空间中的一个非零向量,且表示n的有向线段所在的直线与平面α垂直,则称n为平面α的一个法向量.此时,也称n与平面α垂直,记作n⊥α.
微思考
一个平面的法向量是否唯一?
提示:不唯一,一个平面的法向量有无数多个.
激趣诱思
知识点拨
2.平面的法向量的求法
在空间直角坐标系下,求平面的法向量的一般步骤:
(1)设平面的法向量为n=(x,y,z);
(2)找出(求出)平面内的两个不共线的向量a=(a1,b1,c1),b=(a2,b2,c2);
(4)解方程组,取其中的一组解,即得平面的一个法向量.
激趣诱思
知识点拨
微练习
点A(a,0,0),B(0,b,0),C(0,0,c),则平面ABC的一个法向量为( )
A.(bc,ac,ab) B.(ac,ab,bc)
C.(bc,ab,ac) D.(ab,ac,bc)
答案:A
激趣诱思
知识点拨
3.用空间向量处理平行或垂直关系
(1)如果v是直线l的一个方向向量,n是平面α的一个法向量,则n∥v?l⊥α;n⊥v?l∥α,或l?α.
(2)如果n1是平面α1的一个法向量,n2是平面α2的一个法向量,则
n1⊥n2?α1⊥α2;n1∥n2?α1∥α2,或α1与α2重合.
名师点析 解答这类问题的关键:一是要清楚直线的方向向量,平面的法向量和直线、平面的位置关系之间的内在联系;二是熟练掌握判断向量共线、垂直的方法.在把向量问题转化为几何问题时,要注意两者的区别,直线的方向向量和平面平行,则直线可能在平面内,也可能与平面平行.
激趣诱思
知识点拨
微练习
设直线l的一个方向向量d=(6,2,3),平面α的一个法向量n=(-1,3,0),则直线l与平面α的位置关系是( )
A.垂直 B.平行
C.直线l在平面α内 D.直线l在平面α内或平行
答案:D
激趣诱思
知识点拨
微判断
(1)若平面外的一条直线的方向向量与平面的法向量垂直,则该直线与平面平行.( )
(2)直线的方向向量与平面的法向量的方向相同或相反时,直线与平面垂直.( )
(3)两个平面的法向量平行,则这两个平面平行或重合;两个平面的法向量垂直,则这两个平面垂直.( )
答案:(1)√ (2)√ (3)√
激趣诱思
知识点拨
4.三垂线定理及三垂线定理的逆定理
三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直.
三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直.
微思考
三垂线定理及其逆定理有何区别与联系?
提示:联系:都是一面四线,三种垂直关系.
区别:①从条件或结论上看,三垂线定理是“线与射影垂直?线与斜线垂直”,而逆定理恰好相反;②从作用上看,三垂线定理是“共面直线垂直?异面直线垂直”,而逆定理恰好相反.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
求平面的法向量
例1
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.AB=AP=1,AD= ,试建立恰当的空间直角坐标系,求平面ACE的一个法向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 通过此类例题的解答,在求平面的法向量时要注意:
(1)选向量:在选取平面内的向量时,要选取不共线的两个向量.
(2)取特值:在求n的坐标时,可令x,y,z中一个为特殊值得另两个值,得到平面的一个法向量.
(3)注意0:提前假定法向量n=(x,y,z)的某个坐标为某特定值时一定要注意这个坐标不为0.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
延伸探究 本例条件不变,试求直线PC的一个方向向量和平面PCD的一个法向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练1已知△ABC的三个顶点的坐标分别为A(2,1,0),B(0,2,3),C(1,1,3),试求出平面ABC的一个法向量.
解:设平面ABC的法向量为n=(x,y,z).
∵A(2,1,0),B(0,2,3),C(1,1,3),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
利用空间向量证明平行问题
例2已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:(1)建立如图所示的空间直角坐标系Dxyz,
则D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 证明线面、面面平行问题的方法
(1)用向量法证明线面平行:①证明直线的方向向量与平面内的某一向量是共线向量且直线不在平面内;②证明直线的方向向量可以用平面内两个不共线向量表示且直线不在平面内;③证明直线的方向向量与平面的法向量垂直且直线不在平面内,如(1)中,FC1?平面ADE一定不能漏掉.
(2)利用空间向量证明面面平行,通常是证明两平面的法向量平行.当然要注意当法向量坐标中有0时,要使用n1=λn2这一形式.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练2
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC= AD=1,问在棱PD上是否存在一点E,使CE∥平面PAB?若存在,求出E点的位置;若不存在,请说明理由.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
解:存在点E使CE∥平面PAB.
以A为坐标原点,分别以AB,AD,AP所在直线为x轴,y轴,z轴建立空间直角坐标系Axyz,
∴P(0,0,1),C(1,1,0),D(0,2,0),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明线面垂直问题
例3如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:如图所示,取BC的中点O,连接AO.
因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,且平面ABC∩平面BCC1B1=BC,AO?平面ABC,所以AO⊥平面BCC1B1.
取B1C1的中点O1,以O为坐标原点,OB,OO1,OA所在直线分别为x轴,y轴,z轴,建立空间直角坐标系Oxyz,
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 1.用坐标法证明线面垂直的常用方法:
方法一:基向量法
(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)找出平面内两条相交直线,并用坐标表示它们的方向向量.
(4)分别计算两组向量的数量积,得到数量积为0.
方法二:坐标法
(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)求出平面的法向量.
(4)判断直线的方向向量与平面的法向量平行.
2.对于容易建系的几何载体要尽量用坐标法处理有关垂直问题,如果只用基向量法解决涉及的线性运算和数量积运算比较复杂.而建系后只需一切交给坐标即可.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
延伸探究 本例中增加条件,E,F分别是BC,BB1的中点,求证:EF⊥平面ADE.
即EF⊥EA,EF⊥ED,
又EA∩ED=E,EA,ED?平面ADE,
∴EF⊥平面ADE.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练3如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:方法一 设正方体的棱长为2,建立如图所示的空间直角坐标系,
则A(2,0,0),C(0,2,0),B1(2,2,2),E(2,2,1),F(1,1,2).
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明面面垂直问题
例4
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,
求证:平面ADE⊥平面ABE.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:取BE的中点O,连接OC,又AB⊥平面BCE,所以以O为原点建立空间直角坐标系Oxyz(如图所示).
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
又AB⊥平面BCE,OC?平面BCE,
所以AB⊥OC.
因为BE⊥OC,AB∩BE=B,AB,BE?平面ABE,
所以OC⊥平面ABE.
反思感悟 证明面面垂直的两种方法
(1)常规法:利用面面垂直的判定定理转化为线面垂直、线线垂直去证明.
(2)向量法:证明两个平面的法向量互相垂直.此例就是用的向量法,关键是明确两个平面的法向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练4在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在直线AE上求一点M,使得A1M⊥平面AED.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
(1)证明:以D为坐标原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系Dxyz.
设正方体的棱长为2,则D(0,0,0),A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2),D1(0,0,2),
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
三垂线定理及其逆定理
例5如图,空间四边形ABCD中,点A在平面BCD内的射影 O1是△BCD的垂心,求证:B在平面ACD内的射影O2必是△ACD的垂心.
分析应用三垂线定理一定要分清斜线与射影,并注意第三条垂线要与射影在同一平面内.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
证明:连接DO1,BO1,AO2,CO2.
∵O1是△BCD的垂心,∴DO1⊥BC.
又AO1⊥平面BCD,∴BC⊥AD(三垂线定理).
∵BC是平面ACD的斜线,BO2⊥平面ACD,CO2是BC在平面ACD内的射影,
∴CO2⊥AD(三垂线定理的逆定理).
同理,AO2⊥CD.
∴O2是△ACD的垂心.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 1.三垂线定理及其逆定理常用于判定空间直线互相垂直,在引用时要清楚以下问题:
(1)从条件上看,三垂线定理的条件是“和射影垂直”;其逆定理的条件是“和斜线垂直”.显然本例中三垂线定理和三垂线定理的逆定理都充分利用了.
(2)从功能上看,三垂线定理用于解决已知共面垂直,证明异面垂直的问题;逆定理正好相反.解决垂心问题需要两次垂直的证明,都能用上定理和其逆定理的框架结构.
2.三垂线定理及其逆定理应用中的三个环节
用三垂线定理及其逆定理证明线线垂直的关键在于构造三垂线定理的基本图形,创设应用定理的环境.构造三垂线定理基本图形时要抓住下面三个环节:(1)确定投影面;(2)作出垂线;(3)确定射影.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练5
如图,BC是Rt△ABC的斜边,过点A作△ABC所在平面α的垂线AP,连接PB,PC,过点A作AD⊥BC于点D,连接PD,那么图中的直角三角形共有( )
A.4个 B.6个 C.7个 D.8个
解析:∵AP⊥平面α,
∴PD在平面α内的射影为AD,
∵AD⊥BC,
由三垂线定理可得,PD⊥BC,
∴△ABC,△ABD,△ACD,△PBD,△PCD,△PAB,△PAD,△PAC均为直角三角形,共8个.
故选D.
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练6
如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上.
已知:∠BAC在平面α内,点P在α外,PE⊥AB,PF⊥AC,PO⊥α,垂足分别是E,F,O,PE=PF.
求证:∠BAO=∠CAO.
证明:连接PA,OE,OF.
∵PE⊥AB,PF⊥AC,PO⊥α,
∴AB⊥OE,AC⊥OF(三垂线定理的逆定理),
∵PE=PF,PA=PA,∴Rt△PAE≌Rt△PAF.
∴AE=AF.又AO=AO,∴Rt△AOE≌Rt△AOF.
∴∠BAO=∠CAO.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
平行或垂直证明中的探索类问题
一、平行证明中的探索类问题
案例 1如图所示,在正方体AC1中,O为底面ABCD中心,P是DD1的中点,设Q是CC1上的点,当点Q在什么位置时,平面D1BQ∥平面PAO.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
解:如图所示,分别以DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,在CC1上任取一点Q,连接BQ,D1Q.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
归纳提升(1)求点的坐标:可设出对应点的坐标,根据面面平行的判定定理转化为向量共线问题或者利用两个平面的法向量共线,进而建立与所求点的坐标有关的等式.
(2)由结论推应具备的条件的逆向推理是逻辑推理中的一种基本形式,通过应用推理的方式与方法,能较好地培养学生的合乎逻辑的思维品质.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
二、垂直证明中的探索类问题
案例 2在正方体ABCD-A1B1C1D1中,E是棱BC的中点,试在棱CC1上求一点P,使得平面A1B1P⊥平面C1DE.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
解:如图,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.设正方体的棱长为1,
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
归纳提升立体几何中探索性、存在性问题的思维层次较高,分析时应特别注意.本例由题意设出探求点的坐标,利用两平面垂直,法向量的位置关系及严密的逻辑推理,从而得出点P的坐标.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
1.若直线l的方向向量a=(1,0,2),平面α的法向量为n=(-2,0,-4),则( )
A.l∥α
B.l⊥α
C.l?α
D.l与α斜交
解析:∵n=-2a,∴a∥n,即l⊥α.
答案:B
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
3.若平面α,β的法向量分别为a=(2,-1,0),b=(-1,-2,0),则α与β的位置关系是( )
A.平行
B.垂直
C.相交但不垂直
D.无法确定
解析:a·b=-2+2+0=0,∴a⊥b,∴α⊥β.
答案:B
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
4.如图,在△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的度数( )
A.逐渐变大 B.逐渐变小
C.不变 D.先变大再变小
解析:由题意可得,AC⊥BC.
∵PA⊥平面ABC,
由三垂线定理的逆定理可得,BC⊥PC.
∴∠PCB=90°,
即∠PCB的度数保持不变.
故选C.
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:①②③
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
6.如图所示,在空间图形P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,CD∥AB,∠ABC=∠BCD=90°,AB=4,CD=1,点M在PB上,且PB=4PM,∠PBC=30°,求证:CM∥平面PAD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
7.在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°,E,F分别是AC,AD的中点,求证:平面BEF⊥平面ABC.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
