人教B版(2019)高中数学选择性必修第一册 1.2.4 二面角(共33张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 1.2.4 二面角(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 14:43:34 | ||
图片预览







文档简介
1.2.4 二面角
核心素养
1.掌握二面角的概念.(数学抽象)
2.理解二面角的平面角的含义.(直观想象、逻辑推理)
3.会用向量法解决二面角的计算问题.(数学运算)
思维脉络
激趣诱思
知识点拨
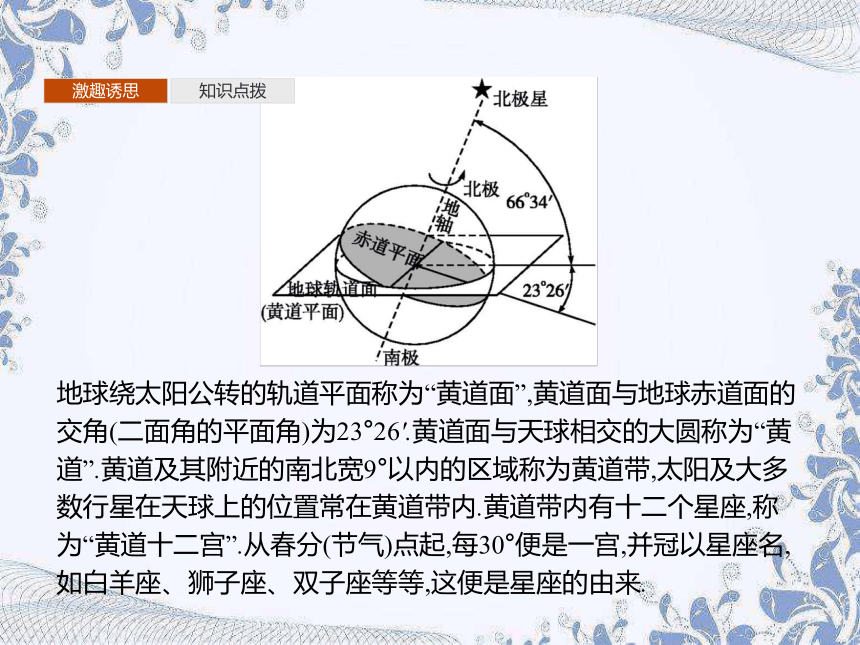
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面的交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆称为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,称为“黄道十二宫”.从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、狮子座、双子座等等,这便是星座的由来.
激趣诱思
知识点拨
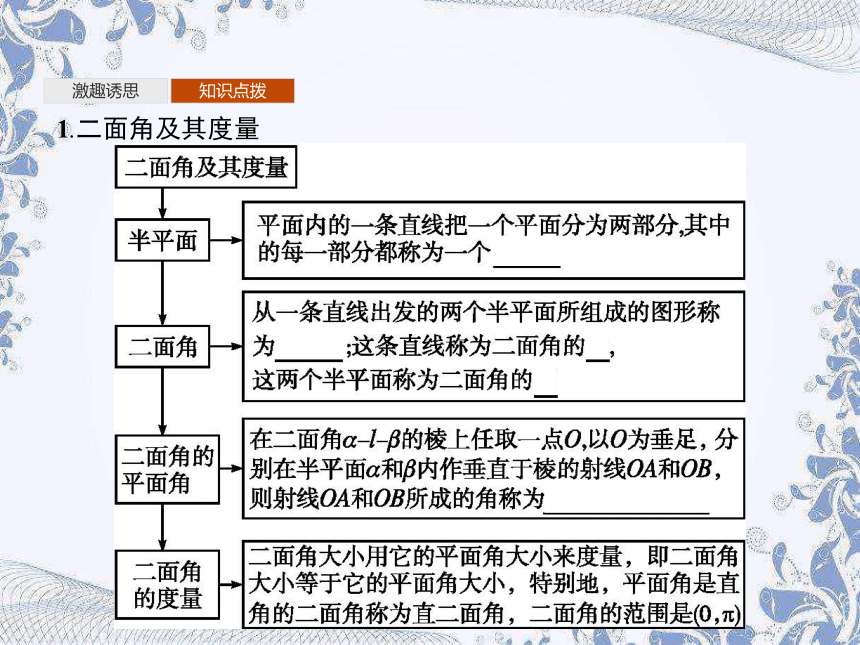
1.二面角及其度量
激趣诱思
知识点拨
微练习
在正方体ABCD-A1B1C1D1中,平面B1C1DA与平面BCDA所成二面角的大小为 .?
答案:45°
微思考
两个平面相交时,它们所成角的取值范围是什么?
提示:(0°,90°]
激趣诱思
知识点拨
2.用空间向量求二面角的大小
(1)如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,则有θ=或θ=π-,特别地,sin θ=sin.
(2)设二面角α-l-β为θ,平面α,β的法向量分别为n1,n2,
激趣诱思
知识点拨
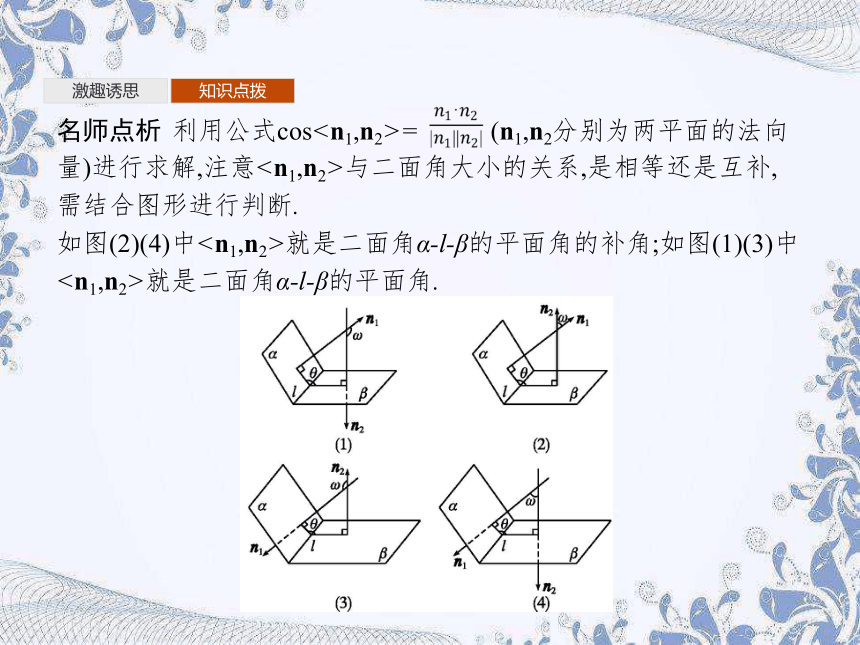
名师点析 利用公式cos= (n1,n2分别为两平面的法向量)进行求解,注意与二面角大小的关系,是相等还是互补,需结合图形进行判断.
如图(2)(4)中就是二面角α-l-β的平面角的补角;如图(1)(3)中就是二面角α-l-β的平面角.
激趣诱思
知识点拨
微判断
(1)二面角的大小就是该二面角两个半平面的法向量的夹角.( )
(2)若二面角两个半平面的法向量的夹角为120°,则该二面角的大小等于60°或120°.( )
答案:(1)× (2)√
激趣诱思
知识点拨
微练习
在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的角的余弦值为( )
激趣诱思
知识点拨
解析:
答案:B
探究一
探究二
素养形成
当堂检测
二面角的平面角问题
例1
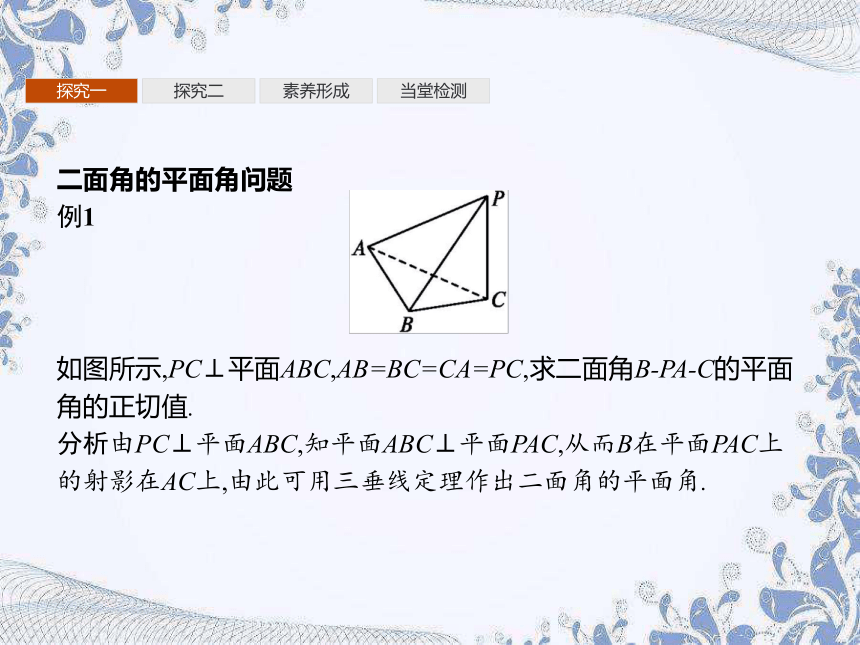
如图所示,PC⊥平面ABC,AB=BC=CA=PC,求二面角B-PA-C的平面角的正切值.
分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射影在AC上,由此可用三垂线定理作出二面角的平面角.
探究一
探究二
素养形成
当堂检测
解:∵PC⊥平面ABC,
∴平面PAC⊥平面ABC,交线为AC.作BD⊥AC于D点,据面面垂直性质定理,BD⊥平面PAC,作DE⊥PA于E点,连接BE,据三垂线定理,则BE⊥PA,从而∠BED是二面角B-PA-C的平面角.
设PC=a,依题意知△ABC是边长为a的正三角形,
探究一
探究二
素养形成
当堂检测
反思感悟 1.本题解法使用了三垂线定理来作出二面角的平面角后,再用解三角形的方法来求解.
2.二面角的定义求法主要有:
(1)由定义作出二面角的平面角;
(2)利用三垂线定理(逆定理)作出二面角的平面角;
(3)作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是二面角的平面角.
探究一
探究二
素养形成
当堂检测
变式训练1
如图,已知二面角α-a-β等于120°,PA⊥α,A∈α,PB⊥β,B∈β,求∠APB的大小.
解:设平面PAOB∩α=OA,平面PAOB∩β=OB.
∵PA⊥α,a?α,∴PA⊥a.
同理PB⊥a.∴a⊥平面PAOB.
又∵OA?平面PAOB,∴a⊥OA.
同理a⊥OB.
∴∠AOB是二面角α-a-β的平面角.
在四边形PAOB中,∠AOB=120°,
∠PAO=∠PBO=90°,所以∠APB=60°.
探究一
探究二
素养形成
当堂检测
利用空间向量求二面角
例2
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1-OB1-D的余弦值.
探究一
探究二
素养形成
当堂检测
(1)证明:因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,
又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,
因为AC∩BD=O,所以O1O⊥底面ABCD.
(2)解:因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD,又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.
如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.
设棱长为2,因为∠CBA=60°,
所以OB= ,OC=1,
所以O(0,0,0),B1( ,0,2),C1(0,1,2),
平面CB1D的一个法向量为n=(0,1,0),
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
反思感悟 利用向量方法求二面角的大小时,多采用求法向量的方法,即求出两个面的法向量,然后通过法向量的夹角来得到二面角的大小,但利用这种方法求解时,要注意结合图形观察分析,确定二面角是锐二面角还是钝二面角,不能将两个法向量的夹角与二面角的大小完全等同起来.
探究一
探究二
素养形成
当堂检测
延伸探究 如果本例条件不变,求二面角B-A1C-D的余弦值.
探究一
探究二
素养形成
当堂检测
变式训练2如图所示,在几何体S-ABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,求平面SAD与平面SAB所成角的余弦值.
探究一
探究二
素养形成
当堂检测
解:如图,过点D作DC的垂线交SC于E,以D为原点,以DC,DE,DA所在直线分别为x,y,z轴建立空间直角坐标系.
∵∠SDC=120°,∴∠SDE=30°,又SD=2,∴点S到y轴的距离为1,
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
用逆向思维解决二面角问题
案例
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,A1A=6,且A1A⊥底面ABCD,点P,Q分别在棱DD1,BC上.
(1)若P是DD1的中点,证明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二面角P-QD-A的余弦值为 ,求四面体ADPQ的体积.
探究一
探究二
素养形成
当堂检测
(1)证明:
由题设知,AA1,AB,AD两两垂直,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则相关各点的坐标为A(0,0,0),B1(3,0,6),D(0,6,0),D1(0,3,6),Q(6,m,0),其中m=BQ,0≤m≤6.
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
归纳提升此类问题属于结论探索类问题.解决此类问题要注意分析题目的整体结构,在此基础上建立空间直角坐标系,引入参数,将所求问题先转化为一个含参数的方程问题,参数确定后其他问题就迎刃而解.
探究一
探究二
素养形成
当堂检测
1.已知平面α内有一个以AB为直径的圆,PA⊥α,点C在圆周上(异于点A,B),点D,E分别是点A在PC,PB上的射影,则( )
A.∠ADE是二面角A-PC-B的平面角
B.∠AED是二面角A-PB-C的平面角
C.∠DAE是二面角B-PA-C的平面角
D.∠ACB是二面角A-PC-B的平面角
答案:B
探究一
探究二
素养形成
当堂检测
答案:C
探究一
探究二
素养形成
当堂检测
3.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为( )
A.45°
B.135°
C.45°或135°
D.90°
答案:C
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
5.在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD.SA=AB=BC=1,AD= ,求平面SCD与平面SAB所成角的余弦值.
探究一
探究二
素养形成
当堂检测
核心素养
1.掌握二面角的概念.(数学抽象)
2.理解二面角的平面角的含义.(直观想象、逻辑推理)
3.会用向量法解决二面角的计算问题.(数学运算)
思维脉络
激趣诱思
知识点拨
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面的交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆称为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,称为“黄道十二宫”.从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、狮子座、双子座等等,这便是星座的由来.
激趣诱思
知识点拨
1.二面角及其度量
激趣诱思
知识点拨
微练习
在正方体ABCD-A1B1C1D1中,平面B1C1DA与平面BCDA所成二面角的大小为 .?
答案:45°
微思考
两个平面相交时,它们所成角的取值范围是什么?
提示:(0°,90°]
激趣诱思
知识点拨
2.用空间向量求二面角的大小
(1)如果n1,n2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ,则有θ=
(2)设二面角α-l-β为θ,平面α,β的法向量分别为n1,n2,
激趣诱思
知识点拨
名师点析 利用公式cos
如图(2)(4)中
激趣诱思
知识点拨
微判断
(1)二面角的大小就是该二面角两个半平面的法向量的夹角.( )
(2)若二面角两个半平面的法向量的夹角为120°,则该二面角的大小等于60°或120°.( )
答案:(1)× (2)√
激趣诱思
知识点拨
微练习
在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的角的余弦值为( )
激趣诱思
知识点拨
解析:
答案:B
探究一
探究二
素养形成
当堂检测
二面角的平面角问题
例1
如图所示,PC⊥平面ABC,AB=BC=CA=PC,求二面角B-PA-C的平面角的正切值.
分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射影在AC上,由此可用三垂线定理作出二面角的平面角.
探究一
探究二
素养形成
当堂检测
解:∵PC⊥平面ABC,
∴平面PAC⊥平面ABC,交线为AC.作BD⊥AC于D点,据面面垂直性质定理,BD⊥平面PAC,作DE⊥PA于E点,连接BE,据三垂线定理,则BE⊥PA,从而∠BED是二面角B-PA-C的平面角.
设PC=a,依题意知△ABC是边长为a的正三角形,
探究一
探究二
素养形成
当堂检测
反思感悟 1.本题解法使用了三垂线定理来作出二面角的平面角后,再用解三角形的方法来求解.
2.二面角的定义求法主要有:
(1)由定义作出二面角的平面角;
(2)利用三垂线定理(逆定理)作出二面角的平面角;
(3)作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是二面角的平面角.
探究一
探究二
素养形成
当堂检测
变式训练1
如图,已知二面角α-a-β等于120°,PA⊥α,A∈α,PB⊥β,B∈β,求∠APB的大小.
解:设平面PAOB∩α=OA,平面PAOB∩β=OB.
∵PA⊥α,a?α,∴PA⊥a.
同理PB⊥a.∴a⊥平面PAOB.
又∵OA?平面PAOB,∴a⊥OA.
同理a⊥OB.
∴∠AOB是二面角α-a-β的平面角.
在四边形PAOB中,∠AOB=120°,
∠PAO=∠PBO=90°,所以∠APB=60°.
探究一
探究二
素养形成
当堂检测
利用空间向量求二面角
例2
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1-OB1-D的余弦值.
探究一
探究二
素养形成
当堂检测
(1)证明:因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,
又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,
因为AC∩BD=O,所以O1O⊥底面ABCD.
(2)解:因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD,又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.
如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.
设棱长为2,因为∠CBA=60°,
所以OB= ,OC=1,
所以O(0,0,0),B1( ,0,2),C1(0,1,2),
平面CB1D的一个法向量为n=(0,1,0),
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
反思感悟 利用向量方法求二面角的大小时,多采用求法向量的方法,即求出两个面的法向量,然后通过法向量的夹角来得到二面角的大小,但利用这种方法求解时,要注意结合图形观察分析,确定二面角是锐二面角还是钝二面角,不能将两个法向量的夹角与二面角的大小完全等同起来.
探究一
探究二
素养形成
当堂检测
延伸探究 如果本例条件不变,求二面角B-A1C-D的余弦值.
探究一
探究二
素养形成
当堂检测
变式训练2如图所示,在几何体S-ABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,求平面SAD与平面SAB所成角的余弦值.
探究一
探究二
素养形成
当堂检测
解:如图,过点D作DC的垂线交SC于E,以D为原点,以DC,DE,DA所在直线分别为x,y,z轴建立空间直角坐标系.
∵∠SDC=120°,∴∠SDE=30°,又SD=2,∴点S到y轴的距离为1,
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
用逆向思维解决二面角问题
案例
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,A1A=6,且A1A⊥底面ABCD,点P,Q分别在棱DD1,BC上.
(1)若P是DD1的中点,证明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二面角P-QD-A的余弦值为 ,求四面体ADPQ的体积.
探究一
探究二
素养形成
当堂检测
(1)证明:
由题设知,AA1,AB,AD两两垂直,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则相关各点的坐标为A(0,0,0),B1(3,0,6),D(0,6,0),D1(0,3,6),Q(6,m,0),其中m=BQ,0≤m≤6.
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
归纳提升此类问题属于结论探索类问题.解决此类问题要注意分析题目的整体结构,在此基础上建立空间直角坐标系,引入参数,将所求问题先转化为一个含参数的方程问题,参数确定后其他问题就迎刃而解.
探究一
探究二
素养形成
当堂检测
1.已知平面α内有一个以AB为直径的圆,PA⊥α,点C在圆周上(异于点A,B),点D,E分别是点A在PC,PB上的射影,则( )
A.∠ADE是二面角A-PC-B的平面角
B.∠AED是二面角A-PB-C的平面角
C.∠DAE是二面角B-PA-C的平面角
D.∠ACB是二面角A-PC-B的平面角
答案:B
探究一
探究二
素养形成
当堂检测
答案:C
探究一
探究二
素养形成
当堂检测
3.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为( )
A.45°
B.135°
C.45°或135°
D.90°
答案:C
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
5.在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD.SA=AB=BC=1,AD= ,求平面SCD与平面SAB所成角的余弦值.
探究一
探究二
素养形成
当堂检测
