湘教版数学八年级上册 4.4一元一次不等式的应用 课件(16张ppt)
文档属性
| 名称 | 湘教版数学八年级上册 4.4一元一次不等式的应用 课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 16:23:21 | ||
图片预览






文档简介
一元一次不等式(组)
4.4 一元一次不等式的应用
4
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点,如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶 ?(图4-6中数字表示出发点到山顶的路程.)
+ + ≤ 9
去时所花时间+休息时间+回来所花时间≤总时间
解:设从出发点到山顶的距离为xkm.
2
解这个不等式, 得x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
- - ≥900
推进新课
例1
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%.如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
销售额-成本-税费≥纯利润(900元)
解:设每套童装的售价是x元.
解这个不等式, 得 x≥125
答:每天童装的售价至少是125元.
40·x
90×40
40·x·10%
1.2×2
+ ≤4.5
一个人坐下时,不宜提举超过4.5kg的重物,以免受伤.小明坐在书桌前,桌上有两本各重1.2kg的画册和一批每本重0.4kg的记事本.如果小明想坐着搬动这两本画册和一些记事本.问他最多只应搬动多少本记事本?
例2
画册的总重+记事本的总重≤4.5kg
解:设小明应搬动x本记事本,则
解这个不等式,得x≤5.25
根据题意,x取整数,所以x的最大值为5.
答:小明最多只应搬动5本记事本.
0.4x
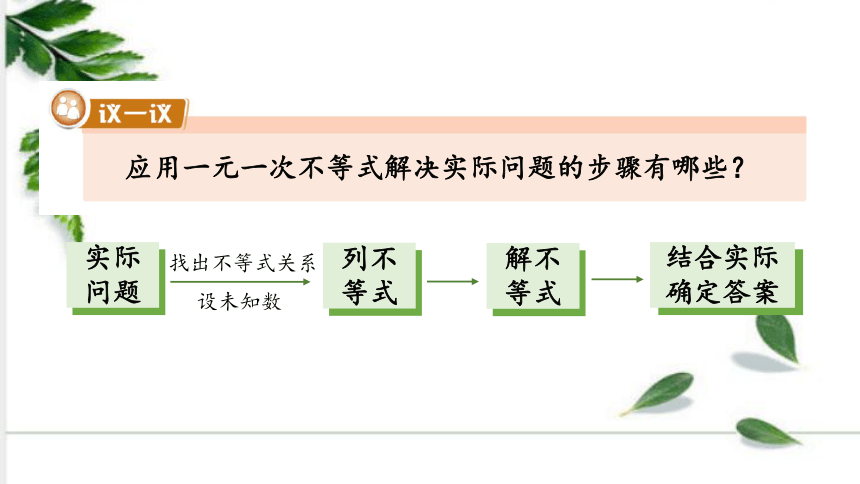
应用一元一次不等式解决实际问题的步骤有哪些?
实际问题
列不等式
解不等式
结合实际确定答案
找出不等式关系
设未知数
巩固练习
解:设至少需要购买x块,则
0.36x≥20
解得 x≥55.6
地板砖数目取整数,所以x的最小值为56
答:至少需要购买56块这样的地板砖.
解:设最多打了xmin电话.
则 0.22+(x-3)×0.11≤0.5
解得 x≤5.5
根据计费标准可知,x的最大值为5.
即她最多打了5min的电话.
“至 多”“最多”“不高于”(“至少”
“最少”“不低于”)对应不等号中的“小于”或“等于”(“大于或等于”),如果是列不等式,那么用“≤”(“≥”)连接.如果是求最后的答案,那么是求解集的最大
(小)值.
知识点睛
3.某厂生产一种零件,每个零件的成本为3元,售价5元,应纳税款为总销售额的10%. 如果要使纯利润不低于3万元,该零件至少要销售多少个?
解:设该零件至少要销售x个.
则 (5-3)x-5x·10%≥30000
解得 x≥20000
答:该零件至少要销售20000个.
4.根据篮球赛的规则,于3分线外投篮命中可得3分,于3分线内投篮命中得2分.若某球队在一场球赛中共投中45个球(只有2分球和3分球),而所得总分不大于100分,问该球队最多投中多少个3分球?
解:设最多投中x个三分球,
则 3x+2(45-x)≤100
解得 x≤10
答:该球队最多投中10个三分球.
5.甲班同学的平均体重是46kg,乙班同学的平均体重42kg,甲、乙两班同学的平均体重不超过44kg.已知甲班有50人,乙班至少有多少人?
解:设乙班至少有x人.
则46×50+42·x≤(50+x)×44
解得 x≥50.
答:乙班至少有50人.
7.某服装厂生产一种西装和领带,已知西装每套定价1200元,领带每条定价200元.厂方为促销,特向客户提供两种优惠方案:
(1)买一套西装送一条领带;
(2)西装和领带均按定价的90%付款.某商店采购员现要到该服装厂购买20套西装,领带x条(x>20).请你根据x的不同情况,帮助该采购员选择最省钱的购买方案.
设y=y1- y2=(20000+200x)-(21600+180x)=20x-1600
当y>0时,即x>80时,方案(2)比方案(1)更省钱.
当y=0时,即x=80时,两种方案相同.
当y<0时,即x<80时,方案(1)比方案(2)更省钱.
7.某服装厂生产一种西装和领带,已知西装每套定价1200元,领带每条定价200元.厂方为促销,特向客户提供两种优惠方案:
(1)买一套西装送一条领带;
(2)西装和领带均按定价的90%付款.某商店采购员现要到该服装厂购买20套西装,领带x条(x>20).请你根据x的不同情况,帮助该采购员选择最省钱的购买方案.
解:按方案(1)购买,应付款y1(元)
其中y1=1200×20+200(x-20)=20000+200x
若按方案(2)购买,应付款y2(元)
其中y2=(1200×20+200x)×90%=21600+180x
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
谢谢!
4.4 一元一次不等式的应用
4
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点,如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶 ?(图4-6中数字表示出发点到山顶的路程.)
+ + ≤ 9
去时所花时间+休息时间+回来所花时间≤总时间
解:设从出发点到山顶的距离为xkm.
2
解这个不等式, 得x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
- - ≥900
推进新课
例1
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%.如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
销售额-成本-税费≥纯利润(900元)
解:设每套童装的售价是x元.
解这个不等式, 得 x≥125
答:每天童装的售价至少是125元.
40·x
90×40
40·x·10%
1.2×2
+ ≤4.5
一个人坐下时,不宜提举超过4.5kg的重物,以免受伤.小明坐在书桌前,桌上有两本各重1.2kg的画册和一批每本重0.4kg的记事本.如果小明想坐着搬动这两本画册和一些记事本.问他最多只应搬动多少本记事本?
例2
画册的总重+记事本的总重≤4.5kg
解:设小明应搬动x本记事本,则
解这个不等式,得x≤5.25
根据题意,x取整数,所以x的最大值为5.
答:小明最多只应搬动5本记事本.
0.4x
应用一元一次不等式解决实际问题的步骤有哪些?
实际问题
列不等式
解不等式
结合实际确定答案
找出不等式关系
设未知数
巩固练习
解:设至少需要购买x块,则
0.36x≥20
解得 x≥55.6
地板砖数目取整数,所以x的最小值为56
答:至少需要购买56块这样的地板砖.
解:设最多打了xmin电话.
则 0.22+(x-3)×0.11≤0.5
解得 x≤5.5
根据计费标准可知,x的最大值为5.
即她最多打了5min的电话.
“至 多”“最多”“不高于”(“至少”
“最少”“不低于”)对应不等号中的“小于”或“等于”(“大于或等于”),如果是列不等式,那么用“≤”(“≥”)连接.如果是求最后的答案,那么是求解集的最大
(小)值.
知识点睛
3.某厂生产一种零件,每个零件的成本为3元,售价5元,应纳税款为总销售额的10%. 如果要使纯利润不低于3万元,该零件至少要销售多少个?
解:设该零件至少要销售x个.
则 (5-3)x-5x·10%≥30000
解得 x≥20000
答:该零件至少要销售20000个.
4.根据篮球赛的规则,于3分线外投篮命中可得3分,于3分线内投篮命中得2分.若某球队在一场球赛中共投中45个球(只有2分球和3分球),而所得总分不大于100分,问该球队最多投中多少个3分球?
解:设最多投中x个三分球,
则 3x+2(45-x)≤100
解得 x≤10
答:该球队最多投中10个三分球.
5.甲班同学的平均体重是46kg,乙班同学的平均体重42kg,甲、乙两班同学的平均体重不超过44kg.已知甲班有50人,乙班至少有多少人?
解:设乙班至少有x人.
则46×50+42·x≤(50+x)×44
解得 x≥50.
答:乙班至少有50人.
7.某服装厂生产一种西装和领带,已知西装每套定价1200元,领带每条定价200元.厂方为促销,特向客户提供两种优惠方案:
(1)买一套西装送一条领带;
(2)西装和领带均按定价的90%付款.某商店采购员现要到该服装厂购买20套西装,领带x条(x>20).请你根据x的不同情况,帮助该采购员选择最省钱的购买方案.
设y=y1- y2=(20000+200x)-(21600+180x)=20x-1600
当y>0时,即x>80时,方案(2)比方案(1)更省钱.
当y=0时,即x=80时,两种方案相同.
当y<0时,即x<80时,方案(1)比方案(2)更省钱.
7.某服装厂生产一种西装和领带,已知西装每套定价1200元,领带每条定价200元.厂方为促销,特向客户提供两种优惠方案:
(1)买一套西装送一条领带;
(2)西装和领带均按定价的90%付款.某商店采购员现要到该服装厂购买20套西装,领带x条(x>20).请你根据x的不同情况,帮助该采购员选择最省钱的购买方案.
解:按方案(1)购买,应付款y1(元)
其中y1=1200×20+200(x-20)=20000+200x
若按方案(2)购买,应付款y2(元)
其中y2=(1200×20+200x)×90%=21600+180x
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
谢谢!
同课章节目录
