第一章 特殊四边形(当堂检测)文

当堂检测(1.1 平行四边形及其性质---课时1)
1.ABCD的四个内角度数的比∠A：∠B：∠C：∠D可以是（ ）
A．2：3：3：2 B．2：3：2：3 C．1：2：3：4 D．2：2：1：1
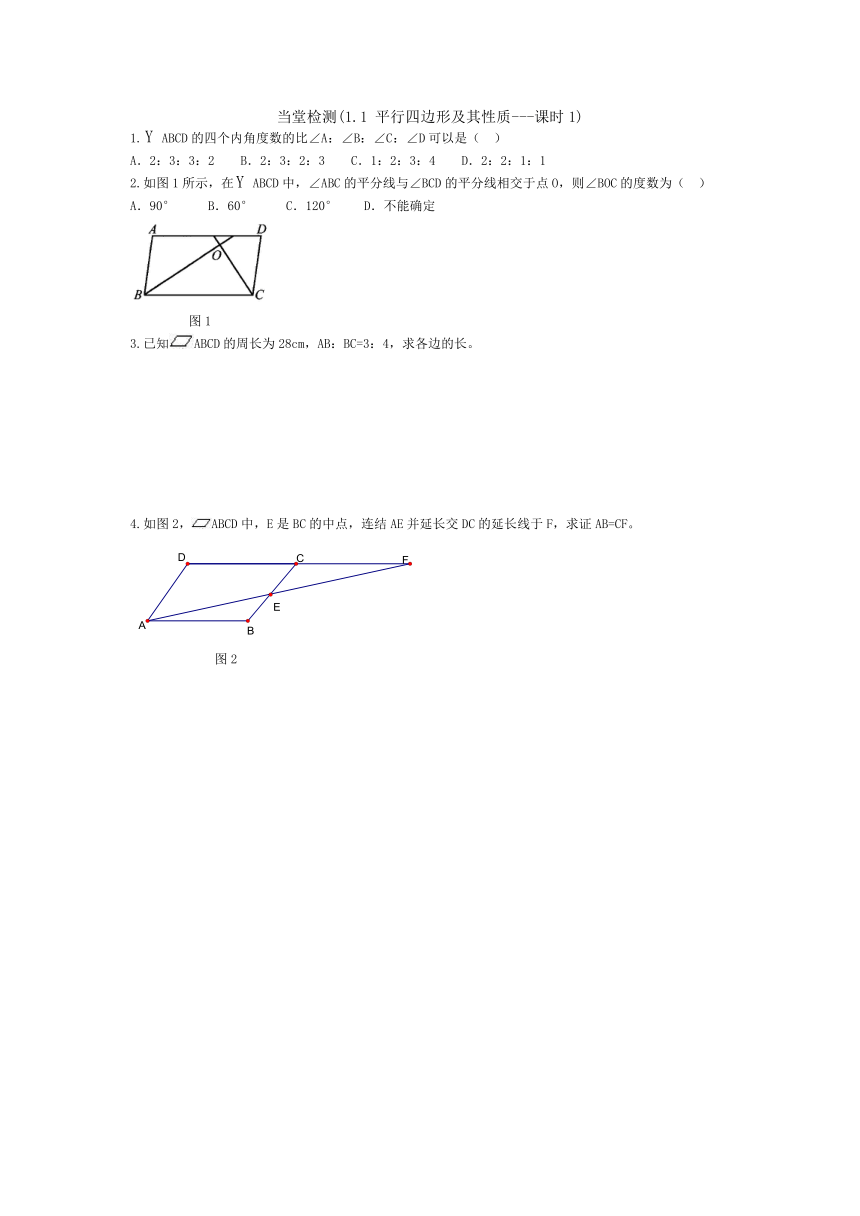
2.如图1所示，在ABCD中，∠ABC的平分线与∠BCD的平分线相交于点O，则∠BOC的度数为（ ）
A．90° B．60° C．120° D．不能确定
图1
3.已知ABCD的周长为28cm，AB：BC=3：4，求各边的长。
4.如图2，ABCD中，E是BC的中点，连结AE并延长交DC的延长线于F，求证AB=CF。
图2
当堂检测(1.1 平行四边形及其性质---课时2)
1. 如图3所示，在ABCD中，对角线交于点，下列式子中一定成立的是（ ）
图3
A． B． C． D．
2.平行四边形的一边长为10，那么它的两条对角线的长可以是（ ）
A.4和6 B.6和8 C. 8和12 D.20和30
3.如图4，平行四边形ABCD的对角线AC和BD相交于O,则其中全等的三角形有______对。
图4
4.如图5，在ABCD 中，已知对角线 AC 和BD相交于点O， △AOB的周长为 15 , AB=6 ，那么对角线 AC与BD的和是多少？
图5
5.一平行四边形两条对角线的长度分别是5cm和7cm，一边长为acm，则a 的取值范围是多少？
当堂检测(1.2平行四边形的判定----课时1)
1. 下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.两组邻角互补的四边形是平行四边形
C.相邻的两角都互补的四边形是平行四边形
D.一组对边平行,一组对角互补的四边形是平行四边形
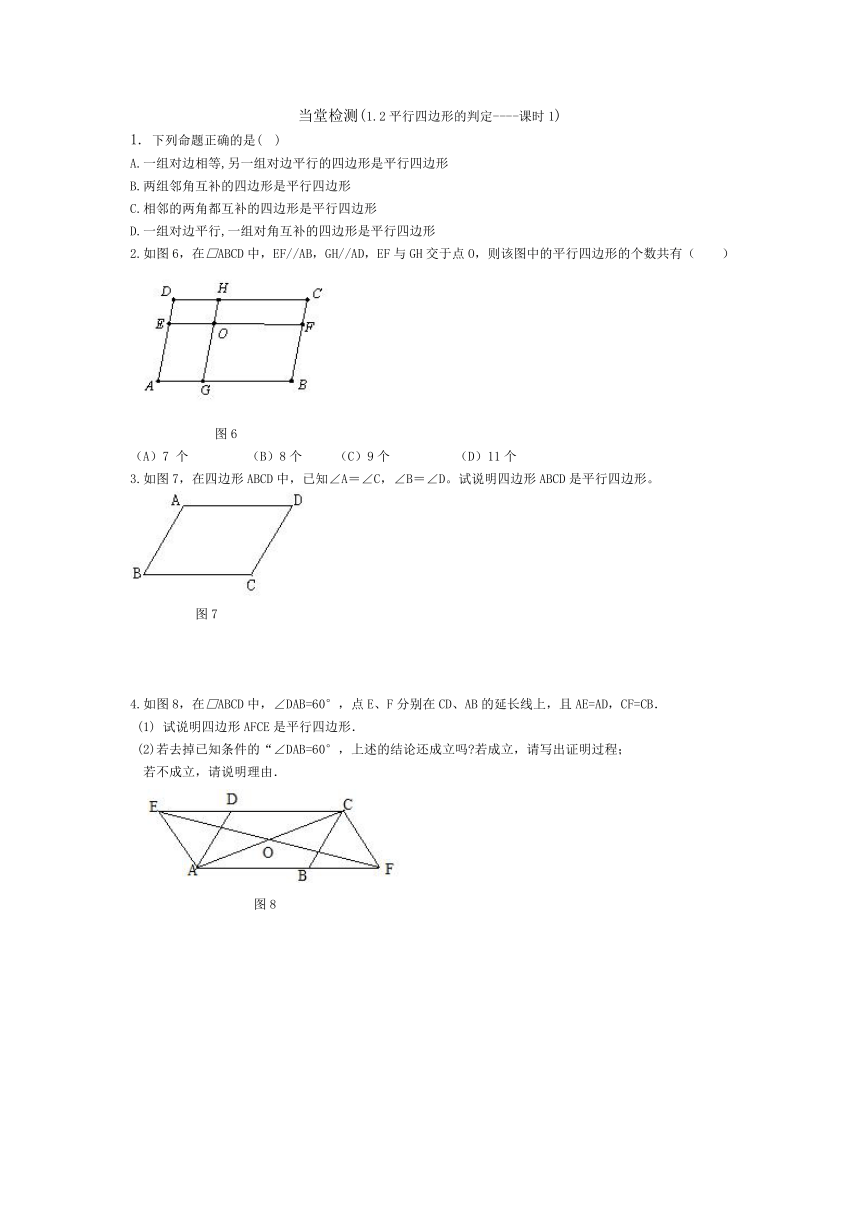
2.如图6，在□ABCD中，EF//AB，GH//AD，EF与GH交于点O，则该图中的平行四边形的个数共有（ ）
图6
（A）7 个 （B）8个 （C）9个 （D）11个
3.如图7，在四边形ABCD中，已知∠A＝∠C，∠B＝∠D。试说明四边形ABCD是平行四边形。
图7
4.如图8，在□ABCD中，∠DAB=60°，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．
(1) 试说明四边形AFCE是平行四边形．
(2)若去掉已知条件的“∠DAB=60°，上述的结论还成立吗 若成立，请写出证明过程；
若不成立，请说明理由．
图8
当堂检测(1.2平行四边形的判定----课时2)
1.下列命题中正确的是( )
A.有两组角分别相等的四边形是平行四边形
B.一组对边平行，一组对角相等的四边形是平行四边形
C.对角线相等的四边形是平行四边形
D.对角线互相垂直的四边形是平行四边形
2.如图9，从□ABCD的各个顶点引对角线的垂线AE、BF、CG、DH，垂足分别是E、F、G、H，连结EF、GH。
图9
求证：EF=HG.
当堂检测(1.3 特殊的平行四边形-----课时1 矩形的性质)
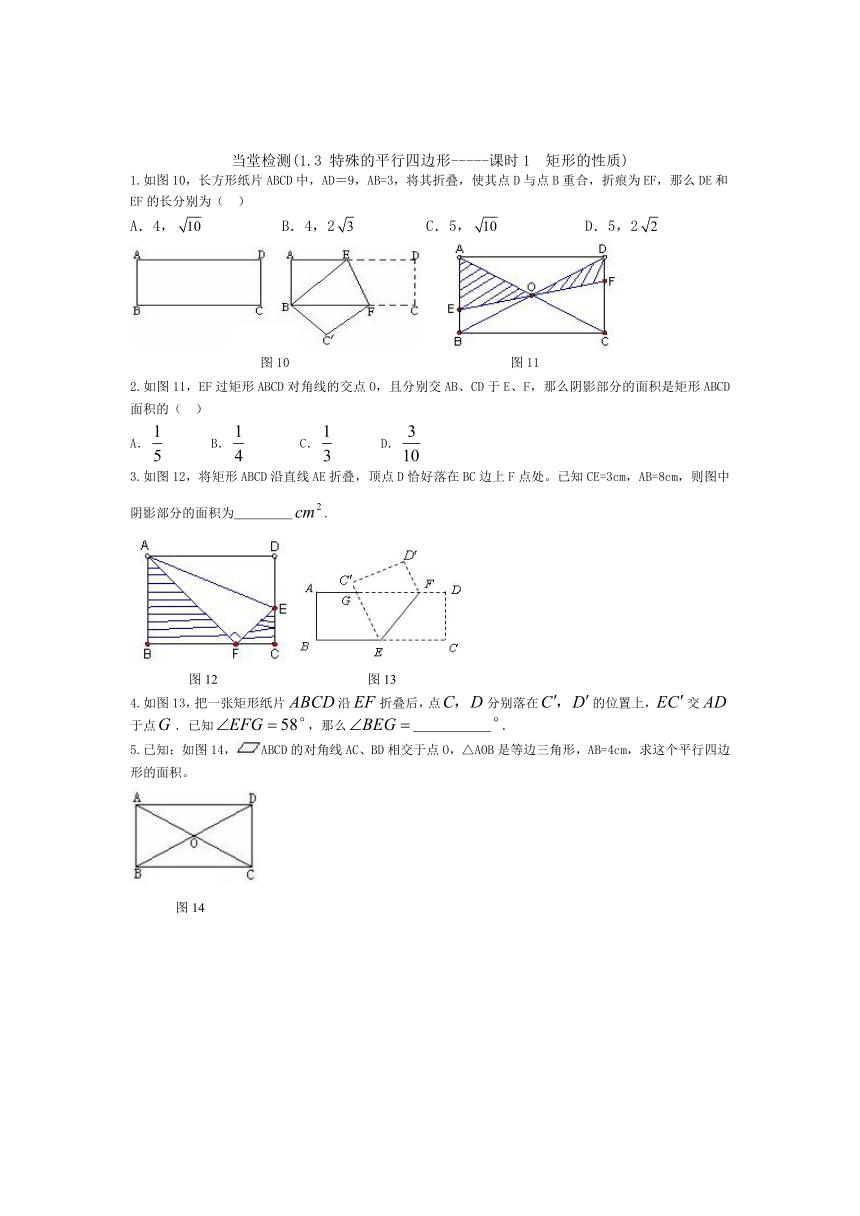
1.如图10，长方形纸片ABCD中，AD＝9，AB=3，将其折叠，使其点D与点B重合，折痕为EF，那么DE和EF的长分别为（ ）
A．4， B．4，2 C．5， D．5，2
图10 图11
2.如图11，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD面积的（ ）
A． B． C． D．
3.如图12，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F点处。已知CE=3cm，AB=8cm，则图中阴影部分的面积为 .
图12 图13
4.如图13，把一张矩形纸片沿折叠后，点分别落在的位置上，交于点．已知，那么 ．
5.已知：如图14，ABCD的对角线AC、BD相交于点O，△AOB是等边三角形，AB=4cm，求这个平行四边形的面积。
图14
当堂检测(1.3 特殊的平行四边形-----课时2 矩形的判定)
1.平行四边形ABCD中，AC，BD是两条对角线，如果添加一个条件，即可推出平行四边形ABCD是矩形，那么这个条件是（ ）
A． AB=BC B．AC=BD C． AC⊥BD D．AB⊥BD
2.(2009甘肃白银)如图15，四边形ABCD是平行四边形，使它为矩形的条件可以是　　　 　．
图15
3.求证：如果平行四边形四个内角的平分线能围成一个四边形，那么这个四边形是矩形。
4.学习了矩形的判定后，小明想用所学的数学知识检验一块木板是不是矩形的，可现在仅有一些足够长的细绳，小明不知道如何测量，你能帮他想办法进行检验吗？请说明理由。
5.如图16，E为矩形ABCD的边AD上一点，且BE=ED，P为对角线BD上一点，PF⊥BE于F， PG⊥AD于G。
图16
求证：PF+PG=AB.
当堂检测(1.3 特殊的平行四边形-----课时3 菱形)
1.(2009年河北)如图17，在菱形ABCD中，AB=5，∠BCD=120°，则对角线AC等于（ ）
A．20 B．15 C．10 D．5
图17 图18 图19
2.如图18，四边形是菱形，过点作的平行线交的延长线于点，则下列式子不成立的是( )
A. B. C. ° D.
3.如图18，四边形中，分别是边的中点．请你添加一个条件，使四边形为菱形，应添加的条件是 ．
4.如图20，已知菱形ABCD中，E是AB的中点，且DE⊥AB，AB=a，
图20
求：（1）∠ABC的度数；（2）对角线AC的长；（3）菱形ABCD的面积。
5.如图21，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．
图21
求证：四边形CDC′E是菱形．
当堂检测(1.3 特殊的平行四边形-----课时4 正方形)
1.(2009湖南郴州)如图22是一张矩形纸片ABCD，AD=10cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=6cm，则CD=（　　）
图22
A．4cm B．6cm C．8cm D．10cm
2.如图23，四边形ABCD是正方形，两条对角线相交于点O，OA=2，则∠AOB=_______,∠OAB=_______,BD =_________,AB=_______.
图23
3.若正方形的对角线长为2cm，则正方形的面积为____。
4.在正方形ABCD中，两条对角线交于点O，∠BAC的平分线交BD于E，若正方形ABCD的周长为16cm，则DE=_____cm.
5.已知：如图24，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE＝∠CBP，BE＝BP，
图24
求证：(1)△CPB≌△AEB；(2) PB⊥BE；
6.已知：如图25，EG、FH过正方形ABCD的对角线的交点O，EG⊥FH。
图25
求证：四边形EFGH是正方形。
当堂检测(1.4图形的中心对称)
1.图26是几种名车的标志，在这几个图形中既是中心对称图又是轴对称图形的是（ ）
图26
A．4个 B．3个 C．2个 D．1个
2.图中的图案都是由字母“m”经过变形、组合而成的，其中不是中心对称图形的是（ ）
3.3张扑克牌如图27（1）所示放在桌子上，小敏把其中一张旋转180 后得到如图27（2）所示，则她所旋转的牌从左数起是（ ）
A．第一张 B．第二张 C．第三张 D．第四张
图27
4.图28是我国古代数学赵爽所著的《勾股圆方图注》中所画的图形，它是由四个相同的直角三角形拼成的，下面关于此图形的说法正确的是( )
图28
A．它是轴对称图形，但不是中心对称图形 B．它是中心对称图形，但不是轴对称图形
C．它既是轴对称图形，又是中心对称图形 D．它既不是轴对称图形，又不是中心对称图形
5.如图29，已知△ABC和过点O的两条互相垂直的直线x、y，画出△ABC关于直线x对称的△A′B′C′，再画出△A′B′C′关于直线y对称的△A″B″C″，△A″B″C″与△ABC是否关于点O成中心对称？
图29
当堂检测(1.5 梯形)
1.课外活动课上，老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝，其面积为450cm2,则对角线所用的竹条至少需（ ）
A. B.30cm C.60cm D.
2.(2009山东临沂)如图30，在等腰梯形ABCD中，，对角线于点O，，垂足分别为E、F，设AD=a，BC=b，则四边形AEFD的周长是（ ）
图30
A． B． C． D．
3.在等腰梯形ABCD中，AB∥DC，AD=BC，已知AD=2，∠A=30°，CD=1则这个等腰梯形的面积是________。
4.在梯形ABCD中，DC∥AB，∠D=90°， AD=4cm,∠B=45°，AC平分∠DAB，求梯形ABCD的面积.
5. 已知：如图31，在等腰中，，，，　垂足分别为点，，连接．
图31
求证：四边形是等腰梯形．
当堂检测(1.6中位线定理-------课时1三角形的中位线)
1.如图32，在中，、分别是、边的中点，且，，，则等于（）
A．5 B．7 C．8 D．12
图32 图33 图34 图35
2.已知△ABC的三条边长分别是9cm，7cm，10cm，那么这个三角形的三条中位线所组成的三角形的周长是（ ）
A. 13cm B. 26cm C. 12cm D. 8cm
3.如图33，任意四边形ABCD各边中点分别是E、F、G、H，若对角线AC、BD的长都为20cm，则四边形EFGH的周长是（ ）
A．80cm B．40cm C．20cm D．10cm
4.已知：如图34，在平行四边形ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于G、H，请判断下列结论： ①BE=DF,②AG=GH=HC,③,④S ABE=3S AGE 其中正确的有（　 ）
A．1个　　B．2个　　C．3个　　D．4个
5.如图35，已知△ABC，D、E、F分别是BC、AB、AC边上的中点。
(1)若△ABC的周长为18cm，它的三条中位线围成的△DEF的周长是________
(2)图中有_____个平行四边形；(3)若∠B=40°，则∠EFD=______
6.已知： 如图36所示，在△ABC中，AD＝DB，BE＝EC，AF＝FC．
试说明 AE、DF互相平分．
图36
当堂检测(1.6中位线定理-------课时2梯形的中位线)
1.如图37(1)为一梯形ABCD，其中∠C=∠D=90°，且AD=6,BC=18，CD=12.将AD叠合在BC上，出现折线MN，如图(2)所示，则MN的长度为( )
图37
A.9 B.12 C.15 D.21
2.直角梯形ABCD，AD∥BC, ∠B=90°，AB=6，中位线EF=5，则梯形ABCD的面积等于______________。
3.一张梯子，相邻横梁之间的距离相等，最上面一根长为30cm，最低端一根长40cm，如果这张梯子共有7根横梁，则横梁的总长是_________________。
4.如图38，梯形ABCD中，AD∥BC，中位线EF交对角线BD于点O，EF=12,且EO:OF=1：2，则BC=_____________。
图38
5.已知：如图39，在梯形ABCD中，AD∥BC，E、F分别为AB、AC的中点，BD与EF交于点G，
图39
求证：GF=.