黑龙江省绥化肇东市第七中学、11中(五四学制)2019-2020学年七年级下学期期末联考数学试题(Word版 含答案)
文档属性
| 名称 | 黑龙江省绥化肇东市第七中学、11中(五四学制)2019-2020学年七年级下学期期末联考数学试题(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览

文档简介
初二数学期末测试题
(满分120分,考试时间90分钟) 2020.7.3
一、选择题(本题共10个小题,每小题3分,共30分)
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
2.在,,,,中,分式的个数为( )
A.2 B.3 C.4 D.5
3.下列代数运算正确的是( )
A.(x3)2=x5 B.(2x)2=2x2 C.(x+1)3?x2=x5 D.x3?x2=x5
4.下列因式分解正确的是( )
A.2x2﹣2=2(x+1)(x﹣1) B.x2+2x﹣1=(x﹣1)2
C.x2+1=(x+1)2 D.x2﹣x+2=x(x﹣1)+2
5.已知点A(a,2013)与点B(2014,b)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
6.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ).
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
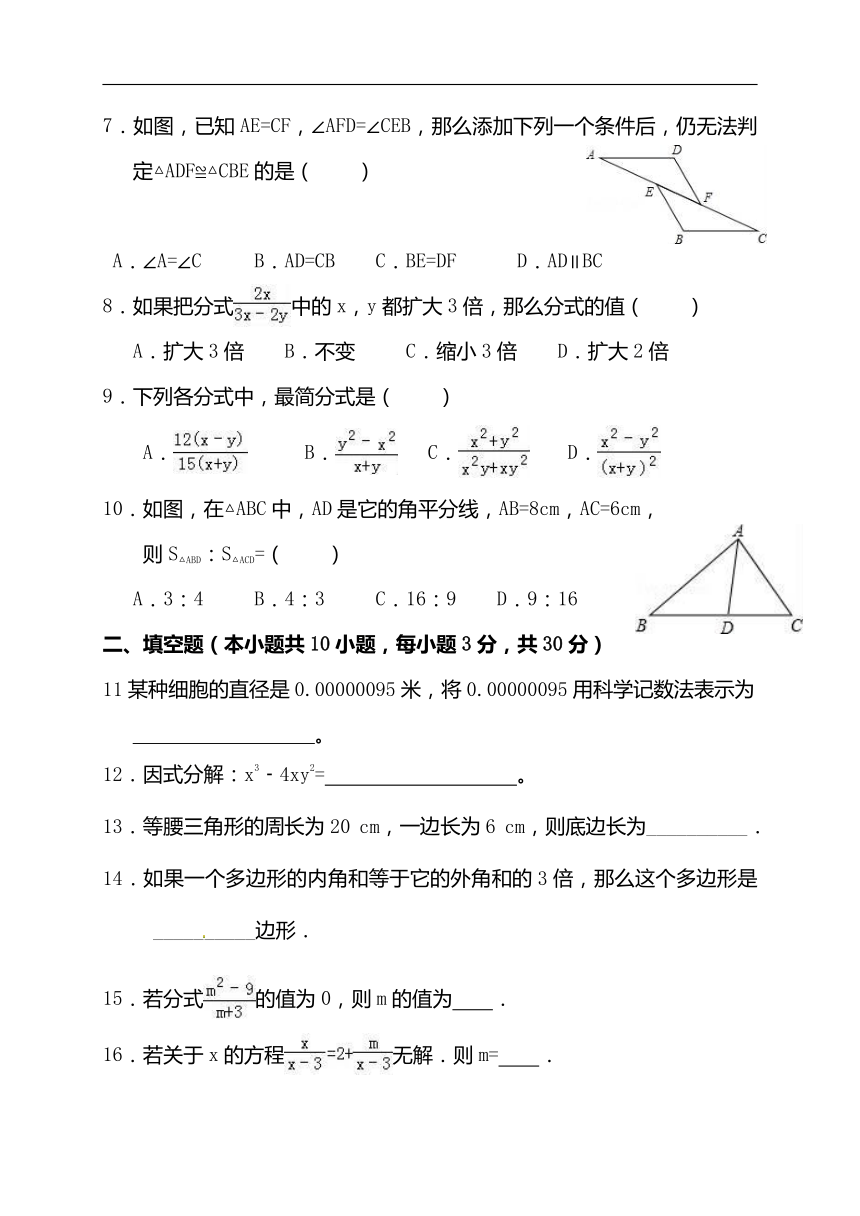
7.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC
8.如果把分式中的x,y都扩大3倍,那么分式的值( )
A.扩大3倍 B.不变 C.缩小3倍 D.扩大2倍
9.下列各分式中,最简分式是( )
A. B. C. D.
10.如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,
则S△ABD:S△ACD=( )
A.3:4 B.4:3 C.16:9 D.9:16
二、填空题(本小题共10小题,每小题3分,共30分)
11某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为
。
12.因式分解:x3﹣4xy2= 。
13.等腰三角形的周长为20 cm,一边长为6 cm,则底边长为__________.
14.如果一个多边形的内角和等于它的外角和的3倍,那么这个多边形是__________边形.
15.若分式的值为0,则m的值为 .
16.若关于x的方程无解.则m= .
17.如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为 cm.
18、=_________.
19、若,则的值为___ .
20、如图,点C在AB上,、均是等边三角形,、分别
与交于点,则下列结论:
① ② ③为等边三角形
④∥正确的有 (填序号)
三、解答题(本大题共8小题60分)
21、计算:(本题共2个小题,每小题4分,共8分)
(1)
(2)
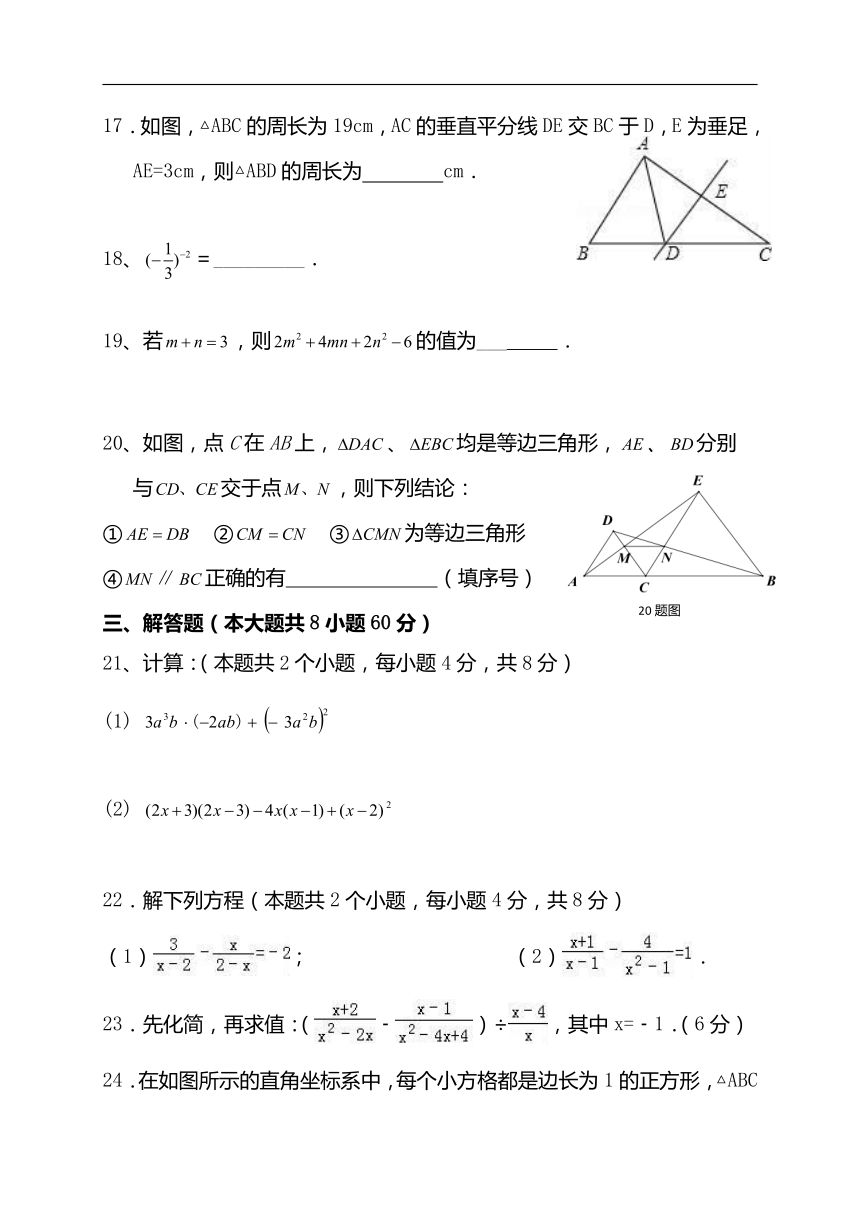
22.解下列方程(本题共2个小题,每小题4分,共8分)
(1); (2).
23.先化简,再求值:(﹣)÷,其中x=﹣1.(6分)
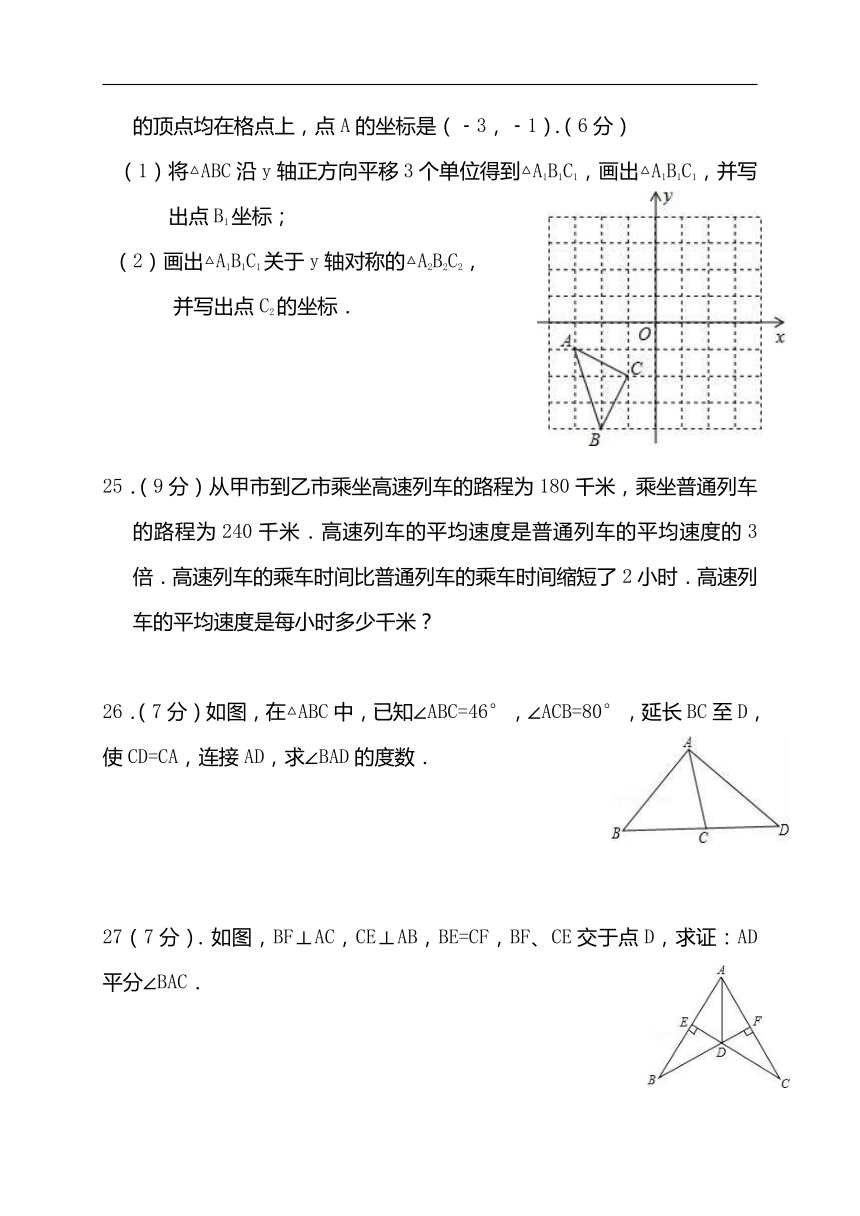
24.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).(6分)
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,
并写出点C2的坐标.
25.(9分)从甲市到乙市乘坐高速列车的路程为180千米,乘坐普通列车的路程为240千米.高速列车的平均速度是普通列车的平均速度的3倍.高速列车的乘车时间比普通列车的乘车时间缩短了2小时.高速列车的平均速度是每小时多少千米?
26.(7分)如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.
27(7分).如图,BF⊥AC,CE⊥AB,BE=CF,BF、CE交于点D,求证:AD平分∠BAC.
28.(9分)如图,正方形ABCD的边长为1,G为CD边上一动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
求证:①△BCG≌△DCE;②BH⊥DE.
八上数学期末测试参考答案
一、选择题(本小题共10小题,每小题3分,共30分)
1A.2A.3D.4A.5B.6 B. 7B.8B.9C . 10B.
二、填空题(本小题共10小题,每小题3分,共30分)
11. 12. x(x+2y)(x﹣2y) .
13.6或8 14.八 15,3 . 16. m= 3 . 17. 13
18.9 19. 12 20①②③④
三、解答题(本大题共8小题,60分)
21 (1) (2)
22.解下列方程
1)解:两边同乘x﹣2,得:3+x=﹣2(x﹣2),
去括号得:3+x=﹣2x+4, 移项合并得:3x=1, 解得:x=,
经检验,x=是原方程的解;
(2)两边同乘(x﹣1)(x+1),得:(x+1)2﹣4=x2﹣1,
去括号得:x2+2x+1﹣4=x2﹣1, 移项合并得:2x=2, 解得:x=1,
经检验,x=1是原方程的增根, 则原方程无解.
23解:原式=[﹣]÷
=[﹣]÷ =÷=×=
当x=﹣1时,原式=.
24.解:(1)如图所示:△A1B1C1,即为所求;点B1坐标为:(﹣2,﹣1);
(2)如图所示:△A2B2C2,即为所求,点C2的坐标为:(1,1).
25.解:设普通列车平均速度每小时x千米,则高速列车平均速度每小时3x千米,
根据题意得,﹣=2, 解得:x=90,
经检验,x=90是所列方程的根, 则3x=3×90=270.
答:高速列车平均速度为每小时270千米.
26.解:∵∠ACB=80° ∴∠ACD=180°﹣∠ACB=180°﹣80°=100°
又∵CD=CA ∴∠CAD=∠D ∵∠ACD+∠CAD+∠D=180° ∴∠CAD=∠D=40°
在△ABC内 ∴∠BAD=180°﹣∠ABC﹣∠D=180°﹣46°﹣40°=94°.
27.证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°.在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),∴DE=DF.∵DF⊥AC,DE⊥AB,∴AD平分∠BAC.
28证明:(1)在正方形ABCD中,∠BCG=90°,BC=CD
在正方形GCEF中,∠DCE=90°,CG=CE 在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS)
(2)∵△BCG≌△DCE,
∴∠1=∠2,∵∠2+∠DEC=90°∴∠1+∠DEC=90°
∴∠BHD=90°
∴BH⊥DE;
(满分120分,考试时间90分钟) 2020.7.3
一、选择题(本题共10个小题,每小题3分,共30分)
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
2.在,,,,中,分式的个数为( )
A.2 B.3 C.4 D.5
3.下列代数运算正确的是( )
A.(x3)2=x5 B.(2x)2=2x2 C.(x+1)3?x2=x5 D.x3?x2=x5
4.下列因式分解正确的是( )
A.2x2﹣2=2(x+1)(x﹣1) B.x2+2x﹣1=(x﹣1)2
C.x2+1=(x+1)2 D.x2﹣x+2=x(x﹣1)+2
5.已知点A(a,2013)与点B(2014,b)关于x轴对称,则a+b的值为( )
A.﹣1 B.1 C.2 D.3
6.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ).
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
7.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC
8.如果把分式中的x,y都扩大3倍,那么分式的值( )
A.扩大3倍 B.不变 C.缩小3倍 D.扩大2倍
9.下列各分式中,最简分式是( )
A. B. C. D.
10.如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,
则S△ABD:S△ACD=( )
A.3:4 B.4:3 C.16:9 D.9:16
二、填空题(本小题共10小题,每小题3分,共30分)
11某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为
。
12.因式分解:x3﹣4xy2= 。
13.等腰三角形的周长为20 cm,一边长为6 cm,则底边长为__________.
14.如果一个多边形的内角和等于它的外角和的3倍,那么这个多边形是__________边形.
15.若分式的值为0,则m的值为 .
16.若关于x的方程无解.则m= .
17.如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为 cm.
18、=_________.
19、若,则的值为___ .
20、如图,点C在AB上,、均是等边三角形,、分别
与交于点,则下列结论:
① ② ③为等边三角形
④∥正确的有 (填序号)
三、解答题(本大题共8小题60分)
21、计算:(本题共2个小题,每小题4分,共8分)
(1)
(2)
22.解下列方程(本题共2个小题,每小题4分,共8分)
(1); (2).
23.先化简,再求值:(﹣)÷,其中x=﹣1.(6分)
24.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).(6分)
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,
并写出点C2的坐标.
25.(9分)从甲市到乙市乘坐高速列车的路程为180千米,乘坐普通列车的路程为240千米.高速列车的平均速度是普通列车的平均速度的3倍.高速列车的乘车时间比普通列车的乘车时间缩短了2小时.高速列车的平均速度是每小时多少千米?
26.(7分)如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.
27(7分).如图,BF⊥AC,CE⊥AB,BE=CF,BF、CE交于点D,求证:AD平分∠BAC.
28.(9分)如图,正方形ABCD的边长为1,G为CD边上一动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
求证:①△BCG≌△DCE;②BH⊥DE.
八上数学期末测试参考答案
一、选择题(本小题共10小题,每小题3分,共30分)
1A.2A.3D.4A.5B.6 B. 7B.8B.9C . 10B.
二、填空题(本小题共10小题,每小题3分,共30分)
11. 12. x(x+2y)(x﹣2y) .
13.6或8 14.八 15,3 . 16. m= 3 . 17. 13
18.9 19. 12 20①②③④
三、解答题(本大题共8小题,60分)
21 (1) (2)
22.解下列方程
1)解:两边同乘x﹣2,得:3+x=﹣2(x﹣2),
去括号得:3+x=﹣2x+4, 移项合并得:3x=1, 解得:x=,
经检验,x=是原方程的解;
(2)两边同乘(x﹣1)(x+1),得:(x+1)2﹣4=x2﹣1,
去括号得:x2+2x+1﹣4=x2﹣1, 移项合并得:2x=2, 解得:x=1,
经检验,x=1是原方程的增根, 则原方程无解.
23解:原式=[﹣]÷
=[﹣]÷ =÷=×=
当x=﹣1时,原式=.
24.解:(1)如图所示:△A1B1C1,即为所求;点B1坐标为:(﹣2,﹣1);
(2)如图所示:△A2B2C2,即为所求,点C2的坐标为:(1,1).
25.解:设普通列车平均速度每小时x千米,则高速列车平均速度每小时3x千米,
根据题意得,﹣=2, 解得:x=90,
经检验,x=90是所列方程的根, 则3x=3×90=270.
答:高速列车平均速度为每小时270千米.
26.解:∵∠ACB=80° ∴∠ACD=180°﹣∠ACB=180°﹣80°=100°
又∵CD=CA ∴∠CAD=∠D ∵∠ACD+∠CAD+∠D=180° ∴∠CAD=∠D=40°
在△ABC内 ∴∠BAD=180°﹣∠ABC﹣∠D=180°﹣46°﹣40°=94°.
27.证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°.在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),∴DE=DF.∵DF⊥AC,DE⊥AB,∴AD平分∠BAC.
28证明:(1)在正方形ABCD中,∠BCG=90°,BC=CD
在正方形GCEF中,∠DCE=90°,CG=CE 在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS)
(2)∵△BCG≌△DCE,
∴∠1=∠2,∵∠2+∠DEC=90°∴∠1+∠DEC=90°
∴∠BHD=90°
∴BH⊥DE;
同课章节目录
