湖南省娄底市娄星区2019-2020学年八年级下学期期末考试数学试题(Word版 含答案)
文档属性
| 名称 | 湖南省娄底市娄星区2019-2020学年八年级下学期期末考试数学试题(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 441.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 11:21:48 | ||
图片预览


文档简介
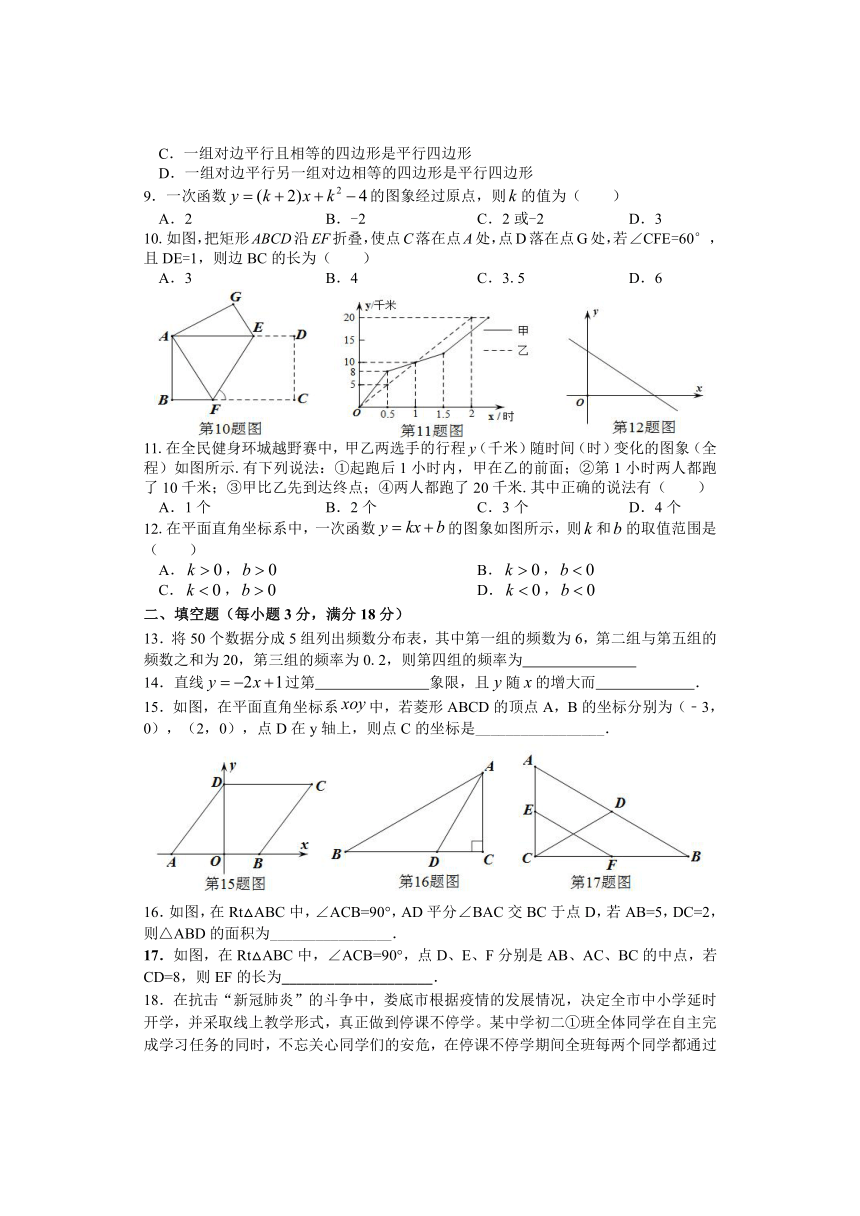
2020年上学期期末文化素质检测试卷
八 年 级 数 学
时量:120分钟 满分:120分 责任人:贺坚章
题号 一 二 三 四 五 六 总分
得分
一、选择题(每小题3分,共12小题,满分36分。每小题给出的四个选项中,只有一个选项是符合题目要求的,请把表示正确答案的字母填入下表中对应的题号下.)
题次 1 2 3 4 5 6 7 8 9 10 11 12
答案
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( ).
2.下列长度的三条线段能组成直角三角形的是( ).
A.2,3,4 B.3,4,5 C.4,5,6 D.6,8,11
3.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,BD=2,则AD的长度是( ).
A.6 B.8 C.12 D.16
4.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
5.如图,在ABCD中,BE平分∠ABC,交AD于点E,AE=3,ED=1,则四边形ABCD的周长为( )
A.10 B.12 C.14 D.16
6.一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360° B.外角和增加360°
C.对角线增加一条 D.内角和增加180°
7.已知P(,)到两坐标轴的距离相等,则的值为( )
A. B.-1 C.或-1 D.或1
8.下列说法中,不正确是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行另一组对边相等的四边形是平行四边形
9.一次函数的图象经过原点,则的值为( )
A.2 B.-2 C.2或-2 D.3
10.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长为( )
A.3 B.4 C.3.5 D.6
11.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
12.在平面直角坐标系中,一次函数的图象如图所示,则和的取值范围是( )
A., B.,
C., D.,
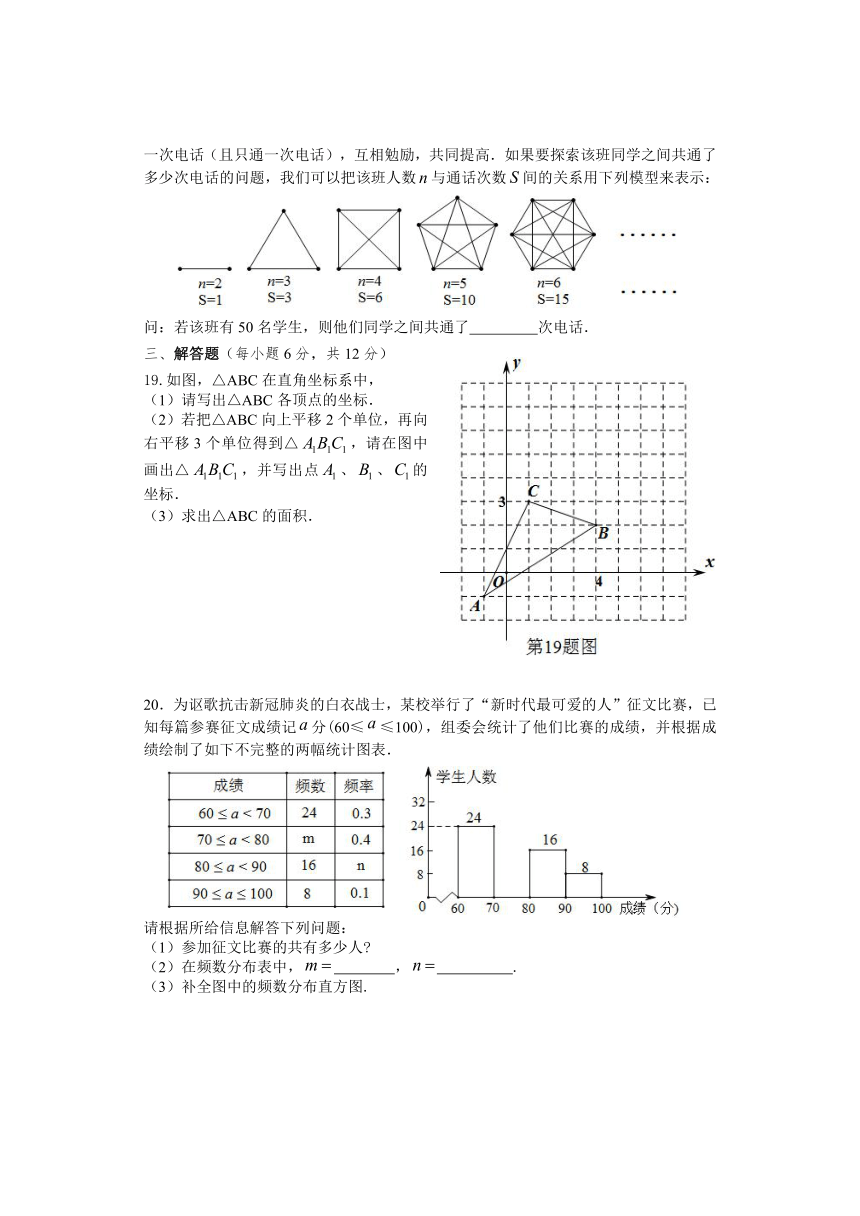
二、填空题(每小题3分,满分18分)
13.将50个数据分成5组列出频数分布表,其中第一组的频数为6,第二组与第五组的频数之和为20,第三组的频率为0.2,则第四组的频率为
14.直线过第 象限,且随的增大而 .
15.如图,在平面直角坐标系中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是_________________.
16.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,若AB=5,DC=2,则△ABD的面积为________________.
17.如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=8,则EF的长为____________________.
18.在抗击“新冠肺炎”的斗争中,娄底市根据疫情的发展情况,决定全市中小学延时开学,并采取线上教学形式,真正做到停课不停学。某中学初二①班全体同学在自主完成学习任务的同时,不忘关心同学们的安危,在停课不停学期间全班每两个同学都通过一次电话(且只通一次电话),互相勉励,共同提高.如果要探索该班同学之间共通了多少次电话的问题,我们可以把该班人数与通话次数间的关系用下列模型来表示:
问:若该班有50名学生,则他们同学之间共通了 次电话.
解答题(每小题6分,共12分)
如图,△ABC在直角坐标系中,
(1)请写出△ABC各顶点的坐标.
(2)若把△ABC向上平移2个单位,再向右平移3个单位得到△,请在图中画出△,并写出点、、的坐标.
(3)求出△ABC的面积.
20.为讴歌抗击新冠肺炎的白衣战士,某校举行了“新时代最可爱的人”征文比赛,已知每篇参赛征文成绩记分(60≤≤100),组委会统计了他们比赛的成绩,并根据成绩绘制了如下不完整的两幅统计图表.
请根据所给信息解答下列问题:
(1)参加征文比赛的共有多少人?
(2)在频数分布表中, , .
(3)补全图中的频数分布直方图.
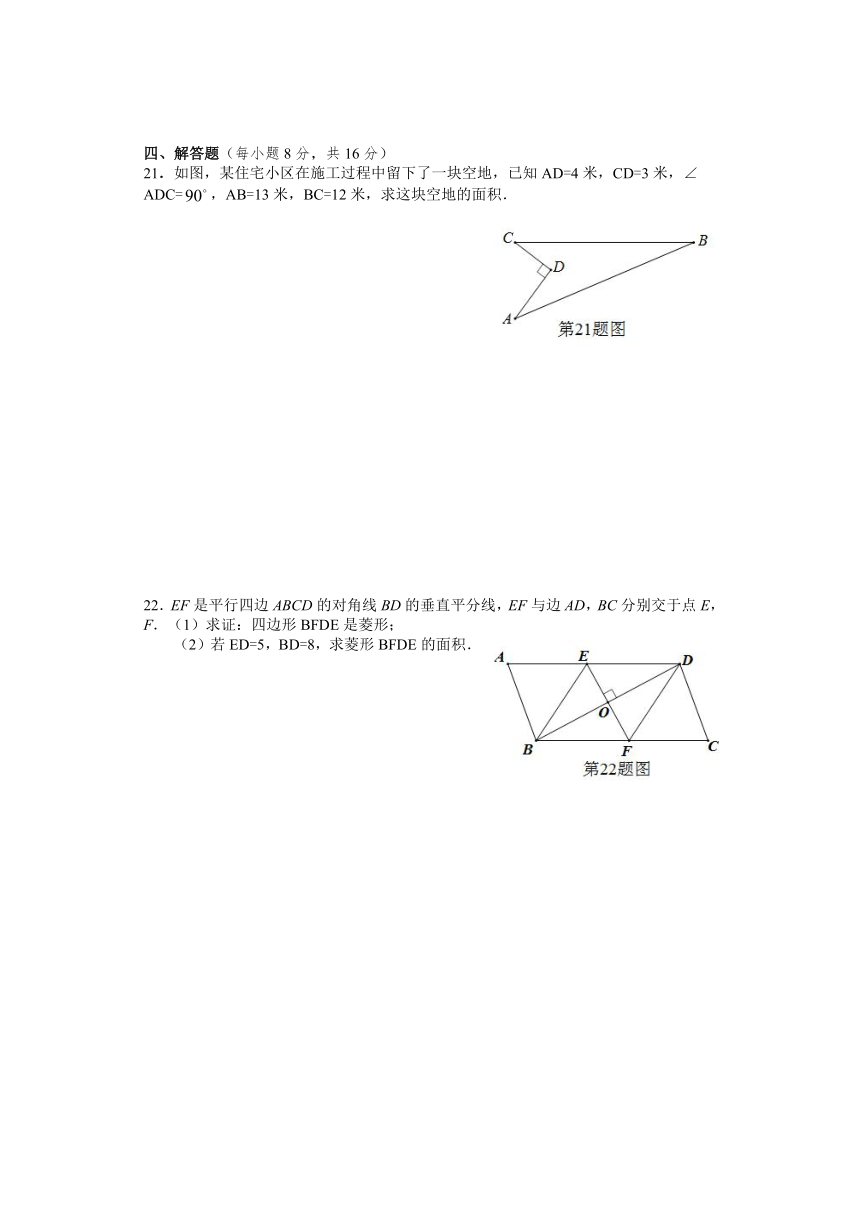
四、解答题(每小题8分,共16分)
21.如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=,AB=13米,BC=12米,求这块空地的面积.
22.EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
五、说理与应用(每小题9分,共2小题,满分18分)
23.甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为(千克),在甲采摘园所需总费用为(元),在乙采摘园所需总费用为(元).
(1)当采摘量超过10千克时,求、与的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
24.有一条笔直公路上有A、B两个停靠站,公路旁有一块山地C正在开发,现在C处时常需要爆破作业。如图,已知A、B两站相距2km,且∠ABC=,∠BAC=,为了安全起见,爆破点C周围半径500米范围内任何人不得进入,问在进行爆破时,公路AB段是否需要暂时封锁?请说明理由.()
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,已知过点B(1,0)的直线与直线:相交于点P(-1,).且与轴相交于C点,与轴相交于A点.
(1)求直线的解析式;
(2)求四边形PAOC的面积;
(3)若点Q是轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
26.阅读题:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解: 如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:如图1,四边形ABCD的对角线AC,BD交于点O,且AC⊥BD,试证明:.
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
2020年上学期八年级数学答案
一、选择题(每小题3分,共12小题,满分36分。每小题给出的四个选项中,只有一个选项是符合题目要求的,请把表示正确答案的字母填入下表中对应的题号下.)
题次 1 2 3 4 5 6 7 8 9 10 11 12
答案 D B A A C D D D A A C C
二、填空题(每小题3分,满分18分)
13.0.28
14.一、二、四, 减少.
15.(5,4)
16.5
17.8
18.1225
解答题(每小题6分,共12分)
如图,△ABC在直角坐标系中,
(1)请写出△ABC各顶点的坐标.
(2)若把△ABC向上平移2个单位,再向右平移3个单位得到△,请在图中画出△,并写出点、、的坐标.
(3)求出△ABC的面积.
解:(1)A (-1,-1) B (4,2) C (1,3)
(2)见图: A1 (2,1) B1 (7,4) C1 (4,5)
⑶ S==7
20.
解:(1)根据题意得:参加征文比赛的的人数为:(人),
答:参加征文比赛的共有80人
(2) m= 80×0.4=32,
n=16÷80=0.2;
故答案为:32,0.2;
(3)由(2)可知,70≤<80段的人数为32人,补全图形:
四、解答题(每小题8分,共16分)
21.如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=,AB=13米,BC=12米,求这块空地的面积.
解:连接AC,
∵ 米,米,
∴AC=(米)
又∵米,米,
∴ AB?=AC?+BC?,
∴△ABC是直角三角形,
∴空地面积S=S△ABC-S△ACD=(平方米)
答:这块空地的面积是24平方米.
22.EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
证明(1)∵四边形ABCD是平行四边形
∴AD∥BC
∴∠EDO=∠FBO,∠DEO=∠BFO
又∵EF是BD的垂直平分线
∴DO=BO
∴△EOD≌△FOB(AAS)
∴ED=BF
易知 ED∥BF
∴ 四边形BFDE是平行四边形
∵ EF⊥BD
∴四边形BFDE是菱形
(2)∵四边形BFDE是菱形,BD=8
∴BO=OD=4
∵ED=5,EF⊥BD
∴在Rt△EOD中,EO=3
∴OF=3,∴EF=6
∴
五、说理与应用(每小题9分,共2小题,满分18分)
23.甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为(千克),在甲采摘园所需总费用为(元),在乙采摘园所需总费用为(元).
(1)当采摘量超过10千克时,求、与的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
解:(1)根据题意得,
y1=60+30×0.6x=60+18x;
y2=10×30+30×0.5(x-10)=150+15x;()
(2)当x=40时,
y1=60+18×40=780,
y2=150+15×40=750,
因为y1>y2,
所以要采摘40千克蓝莓,去乙家比较合算.
答:略
24.有一条笔直公路上有A、B两个停靠站,公路旁有一块山地C正在开发,现在C处时常需要爆破作业。如图,已知A、B两站相距2km,且∠ABC=,∠BAC=,为了安全起见,爆破点C周围半径500米范围内任何人不得进入,问在进行爆破时,公路AB段是否需要暂时封锁?请说明理由.()
解:如图,作CD⊥AB交AB于D点
∵ ∠ABC=,∠BAC=
∴ ∠C=90°
在Rt△ABC中,AB=2, ∠ABC=30°
∴ AC=1
在Rt△ABC中,由勾股定理可得:BC==
又 ∵ 在Rt△BCD中,∠DBC=30°
∴ CD=(km)≈865(m)
∵ CD>500m
∴ 不必封锁
答:公路AB段不需要临时封锁。
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,已知过点B(1,0)的直线与直线:相交于点P(-1,).且与轴相交于C点,与轴相交于A点.
(1)求直线的解析式;
(2)求四边形PAOC的面积;
(3)若点Q是轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
解:(1)∵点P(-1,a)在直线l2:y=2x+4上,
∴,即,则P的坐标为(-1,2),
设直线的解析式为:,
那么,解得:,
∴的解析式为: .
(2)∵直线与y轴相交于点C,∴C的坐标为(0,1).
又∵直线与x轴相交于点A,∴A点的坐标为(-2,0),则AB=3,
∴ .
(3)△QPC周长最小即AQ+CQ的和最小,由“将军饮马”知识可知,作点C关于x轴对称点C′,易求直线:y=-3x-1.当y=0时,x=,∴点Q坐标为(,0)时,△QPC周长最小.
26.阅读题:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解: 如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:如图1,四边形ABCD的对角线AC,BD交于点O,且AC⊥BD,试证明:.
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
证明:(1)四边形ABCD是垂美四边形,理由如下:
如图2,∵AB=AD,
∴点A在线段BD的垂直平分线上.
又∵ CB=CD
∴点C在线段BD的垂直平分线上.
∴ AC是线段BD的垂直平分线,
即 AC⊥BD
所以四边形ABCD是垂美四边形.
如图1,∵AC⊥BD
∴△ODC和△OAB为直角三角形,由勾股定理可得:
,
∴
同理,在Rt△AOD和Rt△BOC中,由勾股定理可得:
, ;
∴
所以有:.
.如图3,连接BE和CG,
∵ ∠GAB=∠GAC+∠CAB=90o+∠CAB
∠CAE=∠BAE+∠CAB=90o+∠CAB
∴ ∠GAB=∠CAE
在△GAB和△CAE中,有:
AG=AC, ∠GAB=∠CAE,AB=AE.
∴ △GAB≌△CAE(SAS)
∴ ∠GBA=∠CEA
在Rt△AEH中,由于∠HAE=90o,
∴ ∠AHE+∠AEH=90o
又∵ ∠OHB=∠AHE,∠GBA=∠CEA
∴ ∠OHB+∠OBH=90o
得: ∠BOH=90o
即:CE⊥BG,
则四边形BCGE是垂美四边形,由(2)可得:
又∵AC=4,AB=5
∴可得:BC=3,,,
则:
=32+50-9
=73
∴
八 年 级 数 学
时量:120分钟 满分:120分 责任人:贺坚章
题号 一 二 三 四 五 六 总分
得分
一、选择题(每小题3分,共12小题,满分36分。每小题给出的四个选项中,只有一个选项是符合题目要求的,请把表示正确答案的字母填入下表中对应的题号下.)
题次 1 2 3 4 5 6 7 8 9 10 11 12
答案
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( ).
2.下列长度的三条线段能组成直角三角形的是( ).
A.2,3,4 B.3,4,5 C.4,5,6 D.6,8,11
3.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,BD=2,则AD的长度是( ).
A.6 B.8 C.12 D.16
4.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
5.如图,在ABCD中,BE平分∠ABC,交AD于点E,AE=3,ED=1,则四边形ABCD的周长为( )
A.10 B.12 C.14 D.16
6.一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360° B.外角和增加360°
C.对角线增加一条 D.内角和增加180°
7.已知P(,)到两坐标轴的距离相等,则的值为( )
A. B.-1 C.或-1 D.或1
8.下列说法中,不正确是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行另一组对边相等的四边形是平行四边形
9.一次函数的图象经过原点,则的值为( )
A.2 B.-2 C.2或-2 D.3
10.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长为( )
A.3 B.4 C.3.5 D.6
11.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
12.在平面直角坐标系中,一次函数的图象如图所示,则和的取值范围是( )
A., B.,
C., D.,
二、填空题(每小题3分,满分18分)
13.将50个数据分成5组列出频数分布表,其中第一组的频数为6,第二组与第五组的频数之和为20,第三组的频率为0.2,则第四组的频率为
14.直线过第 象限,且随的增大而 .
15.如图,在平面直角坐标系中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是_________________.
16.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,若AB=5,DC=2,则△ABD的面积为________________.
17.如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=8,则EF的长为____________________.
18.在抗击“新冠肺炎”的斗争中,娄底市根据疫情的发展情况,决定全市中小学延时开学,并采取线上教学形式,真正做到停课不停学。某中学初二①班全体同学在自主完成学习任务的同时,不忘关心同学们的安危,在停课不停学期间全班每两个同学都通过一次电话(且只通一次电话),互相勉励,共同提高.如果要探索该班同学之间共通了多少次电话的问题,我们可以把该班人数与通话次数间的关系用下列模型来表示:
问:若该班有50名学生,则他们同学之间共通了 次电话.
解答题(每小题6分,共12分)
如图,△ABC在直角坐标系中,
(1)请写出△ABC各顶点的坐标.
(2)若把△ABC向上平移2个单位,再向右平移3个单位得到△,请在图中画出△,并写出点、、的坐标.
(3)求出△ABC的面积.
20.为讴歌抗击新冠肺炎的白衣战士,某校举行了“新时代最可爱的人”征文比赛,已知每篇参赛征文成绩记分(60≤≤100),组委会统计了他们比赛的成绩,并根据成绩绘制了如下不完整的两幅统计图表.
请根据所给信息解答下列问题:
(1)参加征文比赛的共有多少人?
(2)在频数分布表中, , .
(3)补全图中的频数分布直方图.
四、解答题(每小题8分,共16分)
21.如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=,AB=13米,BC=12米,求这块空地的面积.
22.EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
五、说理与应用(每小题9分,共2小题,满分18分)
23.甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为(千克),在甲采摘园所需总费用为(元),在乙采摘园所需总费用为(元).
(1)当采摘量超过10千克时,求、与的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
24.有一条笔直公路上有A、B两个停靠站,公路旁有一块山地C正在开发,现在C处时常需要爆破作业。如图,已知A、B两站相距2km,且∠ABC=,∠BAC=,为了安全起见,爆破点C周围半径500米范围内任何人不得进入,问在进行爆破时,公路AB段是否需要暂时封锁?请说明理由.()
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,已知过点B(1,0)的直线与直线:相交于点P(-1,).且与轴相交于C点,与轴相交于A点.
(1)求直线的解析式;
(2)求四边形PAOC的面积;
(3)若点Q是轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
26.阅读题:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解: 如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:如图1,四边形ABCD的对角线AC,BD交于点O,且AC⊥BD,试证明:.
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
2020年上学期八年级数学答案
一、选择题(每小题3分,共12小题,满分36分。每小题给出的四个选项中,只有一个选项是符合题目要求的,请把表示正确答案的字母填入下表中对应的题号下.)
题次 1 2 3 4 5 6 7 8 9 10 11 12
答案 D B A A C D D D A A C C
二、填空题(每小题3分,满分18分)
13.0.28
14.一、二、四, 减少.
15.(5,4)
16.5
17.8
18.1225
解答题(每小题6分,共12分)
如图,△ABC在直角坐标系中,
(1)请写出△ABC各顶点的坐标.
(2)若把△ABC向上平移2个单位,再向右平移3个单位得到△,请在图中画出△,并写出点、、的坐标.
(3)求出△ABC的面积.
解:(1)A (-1,-1) B (4,2) C (1,3)
(2)见图: A1 (2,1) B1 (7,4) C1 (4,5)
⑶ S==7
20.
解:(1)根据题意得:参加征文比赛的的人数为:(人),
答:参加征文比赛的共有80人
(2) m= 80×0.4=32,
n=16÷80=0.2;
故答案为:32,0.2;
(3)由(2)可知,70≤<80段的人数为32人,补全图形:
四、解答题(每小题8分,共16分)
21.如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=,AB=13米,BC=12米,求这块空地的面积.
解:连接AC,
∵ 米,米,
∴AC=(米)
又∵米,米,
∴ AB?=AC?+BC?,
∴△ABC是直角三角形,
∴空地面积S=S△ABC-S△ACD=(平方米)
答:这块空地的面积是24平方米.
22.EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
证明(1)∵四边形ABCD是平行四边形
∴AD∥BC
∴∠EDO=∠FBO,∠DEO=∠BFO
又∵EF是BD的垂直平分线
∴DO=BO
∴△EOD≌△FOB(AAS)
∴ED=BF
易知 ED∥BF
∴ 四边形BFDE是平行四边形
∵ EF⊥BD
∴四边形BFDE是菱形
(2)∵四边形BFDE是菱形,BD=8
∴BO=OD=4
∵ED=5,EF⊥BD
∴在Rt△EOD中,EO=3
∴OF=3,∴EF=6
∴
五、说理与应用(每小题9分,共2小题,满分18分)
23.甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为(千克),在甲采摘园所需总费用为(元),在乙采摘园所需总费用为(元).
(1)当采摘量超过10千克时,求、与的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
解:(1)根据题意得,
y1=60+30×0.6x=60+18x;
y2=10×30+30×0.5(x-10)=150+15x;()
(2)当x=40时,
y1=60+18×40=780,
y2=150+15×40=750,
因为y1>y2,
所以要采摘40千克蓝莓,去乙家比较合算.
答:略
24.有一条笔直公路上有A、B两个停靠站,公路旁有一块山地C正在开发,现在C处时常需要爆破作业。如图,已知A、B两站相距2km,且∠ABC=,∠BAC=,为了安全起见,爆破点C周围半径500米范围内任何人不得进入,问在进行爆破时,公路AB段是否需要暂时封锁?请说明理由.()
解:如图,作CD⊥AB交AB于D点
∵ ∠ABC=,∠BAC=
∴ ∠C=90°
在Rt△ABC中,AB=2, ∠ABC=30°
∴ AC=1
在Rt△ABC中,由勾股定理可得:BC==
又 ∵ 在Rt△BCD中,∠DBC=30°
∴ CD=(km)≈865(m)
∵ CD>500m
∴ 不必封锁
答:公路AB段不需要临时封锁。
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,已知过点B(1,0)的直线与直线:相交于点P(-1,).且与轴相交于C点,与轴相交于A点.
(1)求直线的解析式;
(2)求四边形PAOC的面积;
(3)若点Q是轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
解:(1)∵点P(-1,a)在直线l2:y=2x+4上,
∴,即,则P的坐标为(-1,2),
设直线的解析式为:,
那么,解得:,
∴的解析式为: .
(2)∵直线与y轴相交于点C,∴C的坐标为(0,1).
又∵直线与x轴相交于点A,∴A点的坐标为(-2,0),则AB=3,
∴ .
(3)△QPC周长最小即AQ+CQ的和最小,由“将军饮马”知识可知,作点C关于x轴对称点C′,易求直线:y=-3x-1.当y=0时,x=,∴点Q坐标为(,0)时,△QPC周长最小.
26.阅读题:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解: 如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:如图1,四边形ABCD的对角线AC,BD交于点O,且AC⊥BD,试证明:.
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
证明:(1)四边形ABCD是垂美四边形,理由如下:
如图2,∵AB=AD,
∴点A在线段BD的垂直平分线上.
又∵ CB=CD
∴点C在线段BD的垂直平分线上.
∴ AC是线段BD的垂直平分线,
即 AC⊥BD
所以四边形ABCD是垂美四边形.
如图1,∵AC⊥BD
∴△ODC和△OAB为直角三角形,由勾股定理可得:
,
∴
同理,在Rt△AOD和Rt△BOC中,由勾股定理可得:
, ;
∴
所以有:.
.如图3,连接BE和CG,
∵ ∠GAB=∠GAC+∠CAB=90o+∠CAB
∠CAE=∠BAE+∠CAB=90o+∠CAB
∴ ∠GAB=∠CAE
在△GAB和△CAE中,有:
AG=AC, ∠GAB=∠CAE,AB=AE.
∴ △GAB≌△CAE(SAS)
∴ ∠GBA=∠CEA
在Rt△AEH中,由于∠HAE=90o,
∴ ∠AHE+∠AEH=90o
又∵ ∠OHB=∠AHE,∠GBA=∠CEA
∴ ∠OHB+∠OBH=90o
得: ∠BOH=90o
即:CE⊥BG,
则四边形BCGE是垂美四边形,由(2)可得:
又∵AC=4,AB=5
∴可得:BC=3,,,
则:
=32+50-9
=73
∴
同课章节目录
