2020秋苏科版九年级数学上册4.3 等可能条件下的概率(二)课件(共16张PPT)
文档属性
| 名称 | 2020秋苏科版九年级数学上册4.3 等可能条件下的概率(二)课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 18:57:58 | ||
图片预览






文档简介
(共16张PPT)
4.3
等可能条件下的概率(二)
第4章
等可能条件下的概率
课程讲授
新知导入
随堂练习
课堂小结
知识要点
几何事件的概率
新知导入
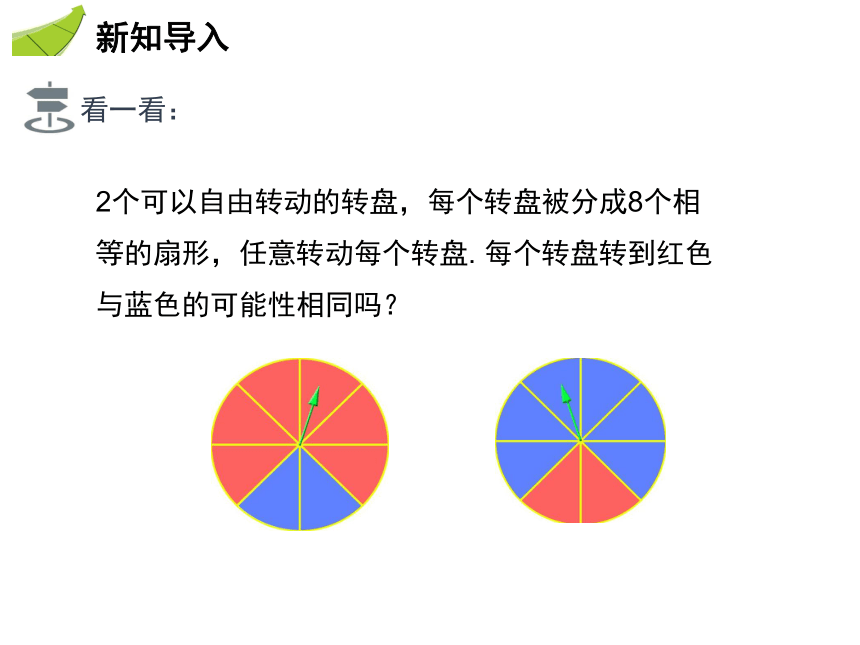
看一看:
2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
每个转盘转到红色与蓝色的可能性相同吗?
课程讲授
1
几何事件的概率
问题1:如图是卧室和书房地板的示意图,图中每一块方砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,并随意停留在某块方砖上.
(1)在哪个房间里,小猫停留在黑砖上的概率大?
卧
室
书
房
课程讲授
1
几何事件的概率
问题1.1:假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是多少?(图中每一块方砖除颜色外完全相同)
P(停在黑砖上)=
课程讲授
1
几何事件的概率
问题1.2:(1)小猫在同样的地板上走来走去,它最终停留在白色方砖上的概率是多少?
(2)小明认为(1)的结果与下面发生的概率相等:袋中装有12个黑球和4个白球,这些球除颜色外都相同,从中任意摸出一球是黑球.你同意吗?
P(停在白砖上)=
同意
课程讲授
1
几何事件的概率
1200
白
红
问题2:如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在白色区域和红色区域的概率分别是多少?
课程讲授
1
几何事件的概率
1200
白
红
指针不是落在白色区域就是落在
红色区域,落在白色区域和红色
区域的概率相等,所以P(落在白色区域)
=P(落在红色区域)=
1200
白
红
课程讲授
1
几何事件的概率
先把白色区域等分成2份,这样转盘被分
成3个扇形区域,其中1个是红色,2个是
白色,所以P(落在红色区域)=
P(落在白色区域)
=
你觉得哪一个是正确的呢?
例1
某商场制作了一个可以自由转动的转盘,转盘被分成24个面积相等的扇形,其中红色扇形1个、蓝色扇形3个、黄色扇形5个、白色扇形15个.
商场规定:顾客每购满1000元商品,可获
得一次转动转盘的机会.当转盘停止转动时
,指针落在红、蓝、黄区域,顾客可分别
获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率是多少?获得500元、100元、50元礼品的概率各是多少?
课程讲授
1
几何事件的概率
课程讲授
1
几何事件的概率
解:
P
(获得礼品)=
8
3
24
5
3
1
=
+
+
24
1
P
(获得500元礼品)=
P
(获得100元礼品)=
24
3
8
1
=
P
(获得50元礼品)=
25
4
提示:由于扇形面积相同,每一种情况出现的概率相同.
随堂练习
1.一儿童行走在如图所示的地板上,当他随意停下时,
最终停在地板上阴影部分的概率是( )
A.
B.
C.
D.
A
随堂练习
2.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是(
)
A.
B.
C.
D.
D
随堂练习
3.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是(
)
A.
B.
C.
D.
C
4.一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为_______.
随堂练习
9
4
课堂小结
几何事件的概率
概率的计算
该事件所占区域的面积
————————————
总面积
4.3
等可能条件下的概率(二)
第4章
等可能条件下的概率
课程讲授
新知导入
随堂练习
课堂小结
知识要点
几何事件的概率
新知导入
看一看:
2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
每个转盘转到红色与蓝色的可能性相同吗?
课程讲授
1
几何事件的概率
问题1:如图是卧室和书房地板的示意图,图中每一块方砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,并随意停留在某块方砖上.
(1)在哪个房间里,小猫停留在黑砖上的概率大?
卧
室
书
房
课程讲授
1
几何事件的概率
问题1.1:假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是多少?(图中每一块方砖除颜色外完全相同)
P(停在黑砖上)=
课程讲授
1
几何事件的概率
问题1.2:(1)小猫在同样的地板上走来走去,它最终停留在白色方砖上的概率是多少?
(2)小明认为(1)的结果与下面发生的概率相等:袋中装有12个黑球和4个白球,这些球除颜色外都相同,从中任意摸出一球是黑球.你同意吗?
P(停在白砖上)=
同意
课程讲授
1
几何事件的概率
1200
白
红
问题2:如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在白色区域和红色区域的概率分别是多少?
课程讲授
1
几何事件的概率
1200
白
红
指针不是落在白色区域就是落在
红色区域,落在白色区域和红色
区域的概率相等,所以P(落在白色区域)
=P(落在红色区域)=
1200
白
红
课程讲授
1
几何事件的概率
先把白色区域等分成2份,这样转盘被分
成3个扇形区域,其中1个是红色,2个是
白色,所以P(落在红色区域)=
P(落在白色区域)
=
你觉得哪一个是正确的呢?
例1
某商场制作了一个可以自由转动的转盘,转盘被分成24个面积相等的扇形,其中红色扇形1个、蓝色扇形3个、黄色扇形5个、白色扇形15个.
商场规定:顾客每购满1000元商品,可获
得一次转动转盘的机会.当转盘停止转动时
,指针落在红、蓝、黄区域,顾客可分别
获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率是多少?获得500元、100元、50元礼品的概率各是多少?
课程讲授
1
几何事件的概率
课程讲授
1
几何事件的概率
解:
P
(获得礼品)=
8
3
24
5
3
1
=
+
+
24
1
P
(获得500元礼品)=
P
(获得100元礼品)=
24
3
8
1
=
P
(获得50元礼品)=
25
4
提示:由于扇形面积相同,每一种情况出现的概率相同.
随堂练习
1.一儿童行走在如图所示的地板上,当他随意停下时,
最终停在地板上阴影部分的概率是( )
A.
B.
C.
D.
A
随堂练习
2.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是(
)
A.
B.
C.
D.
D
随堂练习
3.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是(
)
A.
B.
C.
D.
C
4.一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为_______.
随堂练习
9
4
课堂小结
几何事件的概率
概率的计算
该事件所占区域的面积
————————————
总面积
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
