冀教版九年级数学上册25.1 比例线段课件(共17张PPT)
文档属性
| 名称 | 冀教版九年级数学上册25.1 比例线段课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
25.1
比例线段
课程讲授
新知导入
随堂练习
课堂小结
第二十五章
图形的相似
知识要点
1.成比例线段
2.比例的基本性质
3.黄金分割
新知导入
试一试:根据下列要求,在下图中画出图形并比较.
(1)连接点AB、A1B1、CD和C1D1;
A
B
A1
B1
C
D
C1
D1
(2)比较AB:CD和A1B1:C1D1;
AB:CD
A1B1:C1D1
=
课程讲授
1
成比例线段
问题1:观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
6
3
4
2
4
3
第一个与第二个长方形的形状相同,理由:它们的长与宽的比相等.
课程讲授
1
成比例线段
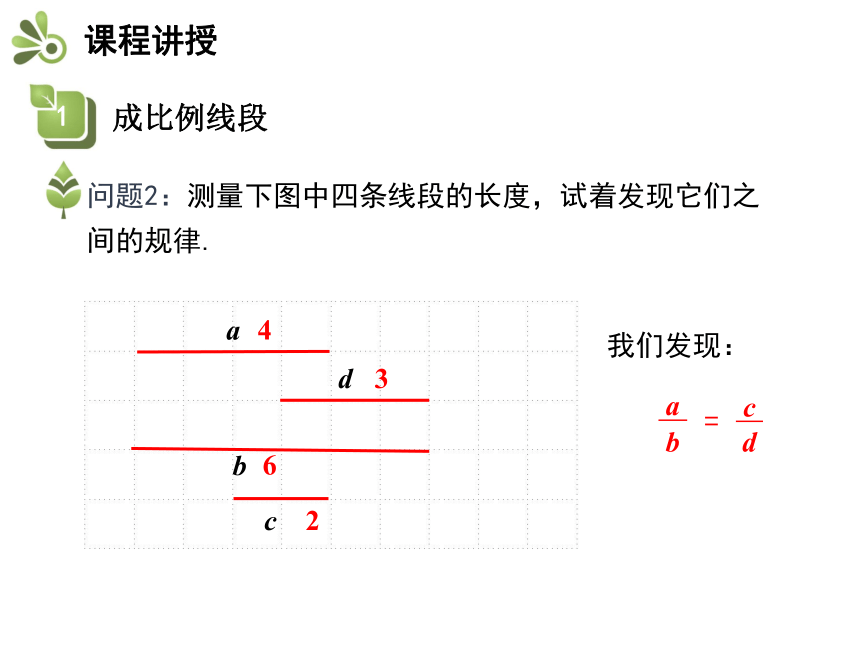
问题2:测量下图中四条线段的长度,试着发现它们之间的规律.
d
a
b
c
3
2
4
6
我们发现:
d
a
b
c
=
课程讲授
1
成比例线段
定义:如果选用同一度量单位,量得线段a和b的长度分
别为m和n,我们就把m和n的比叫做线段a和b的比.
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即
,我们把这四条线段叫做成比例线段,简称比
例线段.
课程讲授
1
成比例线段
练一练:下列各组线段是成比例线段的是(
)
A.2
cm,5
cm,6
cm,8
cm
B.1
cm,2
cm,3
cm,4
cm
C.3
cm,6
cm,7
cm,9
cm
D.3
cm,6
cm,9
cm,18
cm
D
课程讲授
2
比例的基本性质
问题1:如果线段a,b,c,d成比例,那么ad和bc相等吗?为什么?反之,如果线段a,b,c,d满足ad=bc,那么这四条线段成比例吗?
归纳:比例的基本性质:如果
,那么ad=bc.
如果ad=bc,那么
(b,d≠0).
定义:特别地,如果
,即b2=ac,就把b叫做a,c的比例中项.
课程讲授
2
比例的基本性质
问题2:若
,求
的值.
课程讲授
2
比例的基本性质
练一练:已知
(a≠0,b≠0),下列变形错误的是(
)
A.
B.2a=3b
C.
D.3a=2b
A
课程讲授
3
黄金分割
问题:已知线段AB=a,点C在AB上.当
,求线段AC的长.
解:设AC=x,则BC=a-x.依题意,建立方程,得
.
解得
.则AC=
≈0.618a.
课程讲授
3
黄金分割
定义:在线段AB上有一点C,如果点C把AB分成的两条线段AC和BC满足
,那么称线段AB被点C黄金分割,点C称为线段AB的黄金分割点,
称为黄金比.
每条线段上的黄金分割点都有两个.
课程讲授
3
黄金分割
练一练:已知点C是线段AB的黄金分割点,且AB=2,AC<BC,则AC长是( )
A.
B.
C.
D.
C
随堂练习
1.已知
,则
的值为( )
A.
B.
C.
D.
A
随堂练习
2.已知
下列四组数中,不能组成比例的是( )
A.1,2,4,8
B.3,4,5,6
C.
,
,
,
D.0.1,0.3,0.5,1.5
B
随堂练习
3.已知线段a=0.3
m,b=60
cm,c=12
dm.
(1)线段a与线段b的比为________;
(2)如果线段a,b,c,d成比例,那么线段d的长为________cm.
1∶2
240
4.在人体躯和身高的比例上,肚脐是理想的黄金分割点,即(下半身长与身高)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,她应该选择约________cm的高跟鞋看起来更美.(结果保留整数)
8
课堂小结
比例线段
成比例
线段
比例的基本
性质
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即
,我们把这四条线段叫做成比例线段,简称比
例线段.
如果
,那么ad=bc.
如果ad=bc,那么
(b,d≠0).
25.1
比例线段
课程讲授
新知导入
随堂练习
课堂小结
第二十五章
图形的相似
知识要点
1.成比例线段
2.比例的基本性质
3.黄金分割
新知导入
试一试:根据下列要求,在下图中画出图形并比较.
(1)连接点AB、A1B1、CD和C1D1;
A
B
A1
B1
C
D
C1
D1
(2)比较AB:CD和A1B1:C1D1;
AB:CD
A1B1:C1D1
=
课程讲授
1
成比例线段
问题1:观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
6
3
4
2
4
3
第一个与第二个长方形的形状相同,理由:它们的长与宽的比相等.
课程讲授
1
成比例线段
问题2:测量下图中四条线段的长度,试着发现它们之间的规律.
d
a
b
c
3
2
4
6
我们发现:
d
a
b
c
=
课程讲授
1
成比例线段
定义:如果选用同一度量单位,量得线段a和b的长度分
别为m和n,我们就把m和n的比叫做线段a和b的比.
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即
,我们把这四条线段叫做成比例线段,简称比
例线段.
课程讲授
1
成比例线段
练一练:下列各组线段是成比例线段的是(
)
A.2
cm,5
cm,6
cm,8
cm
B.1
cm,2
cm,3
cm,4
cm
C.3
cm,6
cm,7
cm,9
cm
D.3
cm,6
cm,9
cm,18
cm
D
课程讲授
2
比例的基本性质
问题1:如果线段a,b,c,d成比例,那么ad和bc相等吗?为什么?反之,如果线段a,b,c,d满足ad=bc,那么这四条线段成比例吗?
归纳:比例的基本性质:如果
,那么ad=bc.
如果ad=bc,那么
(b,d≠0).
定义:特别地,如果
,即b2=ac,就把b叫做a,c的比例中项.
课程讲授
2
比例的基本性质
问题2:若
,求
的值.
课程讲授
2
比例的基本性质
练一练:已知
(a≠0,b≠0),下列变形错误的是(
)
A.
B.2a=3b
C.
D.3a=2b
A
课程讲授
3
黄金分割
问题:已知线段AB=a,点C在AB上.当
,求线段AC的长.
解:设AC=x,则BC=a-x.依题意,建立方程,得
.
解得
.则AC=
≈0.618a.
课程讲授
3
黄金分割
定义:在线段AB上有一点C,如果点C把AB分成的两条线段AC和BC满足
,那么称线段AB被点C黄金分割,点C称为线段AB的黄金分割点,
称为黄金比.
每条线段上的黄金分割点都有两个.
课程讲授
3
黄金分割
练一练:已知点C是线段AB的黄金分割点,且AB=2,AC<BC,则AC长是( )
A.
B.
C.
D.
C
随堂练习
1.已知
,则
的值为( )
A.
B.
C.
D.
A
随堂练习
2.已知
下列四组数中,不能组成比例的是( )
A.1,2,4,8
B.3,4,5,6
C.
,
,
,
D.0.1,0.3,0.5,1.5
B
随堂练习
3.已知线段a=0.3
m,b=60
cm,c=12
dm.
(1)线段a与线段b的比为________;
(2)如果线段a,b,c,d成比例,那么线段d的长为________cm.
1∶2
240
4.在人体躯和身高的比例上,肚脐是理想的黄金分割点,即(下半身长与身高)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,她应该选择约________cm的高跟鞋看起来更美.(结果保留整数)
8
课堂小结
比例线段
成比例
线段
比例的基本
性质
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即
,我们把这四条线段叫做成比例线段,简称比
例线段.
如果
,那么ad=bc.
如果ad=bc,那么
(b,d≠0).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
