苏科版数学七年级上册 6.5垂直 学案(无答案)
文档属性
| 名称 | 苏科版数学七年级上册 6.5垂直 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-06 00:00:00 | ||
图片预览



文档简介
苏科版数学七年级上册 6.5垂直
个性化辅导讲义
—
学生版
授课日期:
学员编号:
年
级:七年级
课
时
数:
学员姓名:
辅导科目:数学
学科教师:
垂直
【学习目标】
1、进一步丰富对两条直线互相平行或垂直的认识,理解平行线、垂线、垂线段的概念;
2、掌握平行线的判定定理与性质定理;
3、培养学生探索精神,发散其思维.
【知识精讲】
一、相交线
1.直线的位置关系
在同一平面内直线与直线的位置关系只有两种:相交和平行.
2.垂线
当两条直角相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
3.垂线的性质
基本事实:过一点有且只有一条直线与已知直线垂直.
4.垂线段最短
直线外一点与直线上各点连接的所有线段中,垂线段最短.
5.点到直线的距离
直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
二、平行线
1.平行公理
基本事实:过直线外一点有且只有一条直线与这条直线平行.
2.平行线的判定
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行.
3.平行线的性质
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补.
【基础练习】
1、判别下列说法是否正确,并说明理由:
⑴不相交的两条直线是平行线;
(
)
⑵在同一平面内,两条不相交的线段是平行线;(
)
⑶过一点可以而且只可以画一条直线与已知直线平行.(
)
⑷同一平面内的3条直线,它们的交点个数可能是0或1或2或3.(
)
⑸在同一平面内,和第三条直线都不相交的2条直线平行.(
)
⑹过2条相交直线外一点A,能作一条直线与这2条直线都平行.(
)
2、在同一平面内,两条不重合的直线的位置关系只有两种:________、________.
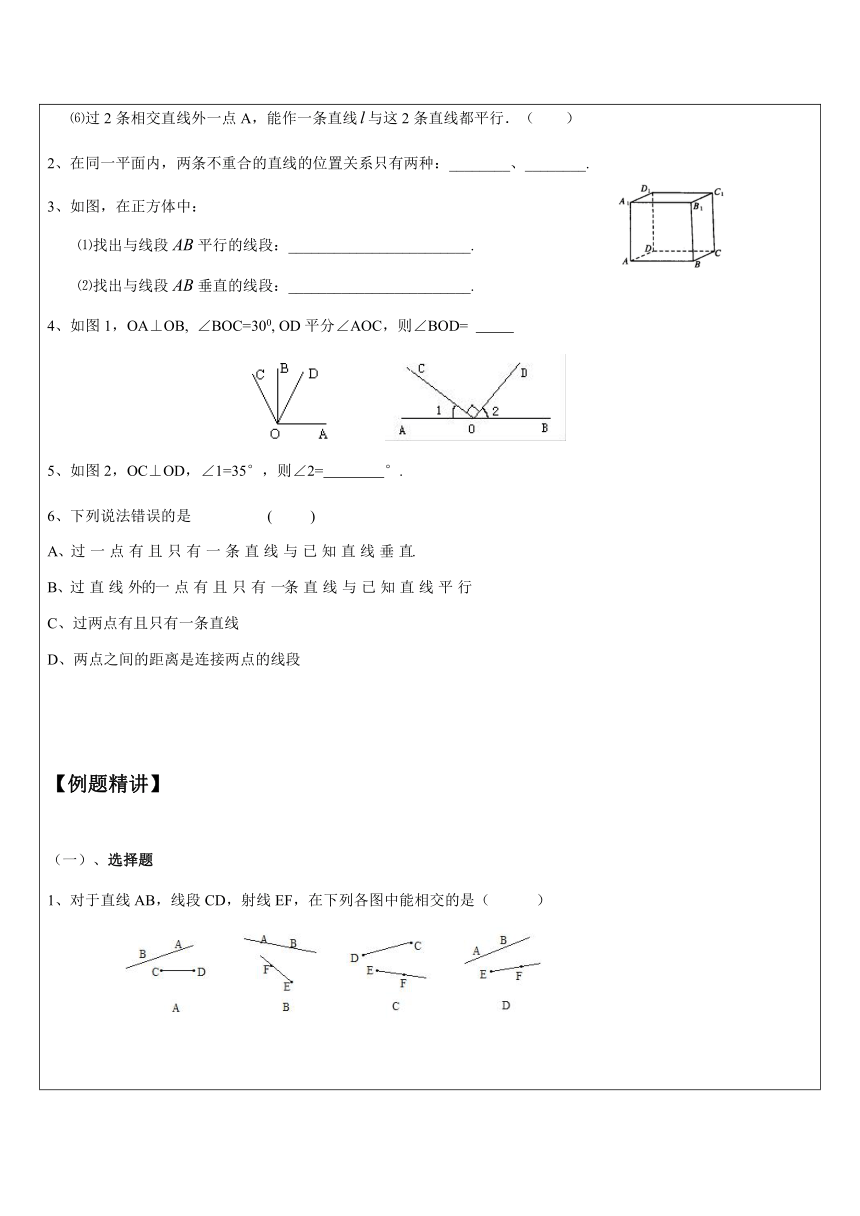
3、如图,在正方体中:
⑴找出与线段平行的线段:________________________.
⑵找出与线段垂直的线段:________________________.
4、如图1,OA⊥OB,
∠BOC=300,
OD平分∠AOC,则∠BOD=
5、如图2,OC⊥OD,∠1=35°,则∠2=
°.
6、下列说法错误的是
(
)
A、过
一
点
有
且
只
有
一
条
直
线
与
已
知
直
线
垂
直.
B、过
直
线
外的一
点
有
且
只
有
一条
直
线
与
已
知
直
线
平
行
C、过两点有且只有一条直线
D、两点之间的距离是连接两点的线段
【例题精讲】
]
(一)、选择题
1、对于直线AB,线段CD,射线EF,在下列各图中能相交的是(
)
2、∠A两边分别垂直于∠B的两边,∠A与∠B的关系是
(
)
A、相等
B、互补
C、相等或互补
D、不能确定
3、如图,将一副三角板叠放在一起,使直角顶点重合于点A,
则∠BAE+∠CAD的度数为
(
)
A、120°
B、135°
C、150°
D、180°
4、下列结论正确的有
(
)
A、如果⊥,⊥,那么⊥
B、⊥,∥,那么∥
C、如果∥,⊥,
那么∥
D、如果⊥,∥,那么⊥
(二)、解答题
1、如图,已知∠ABE
+∠DEB
=
180°,∠1
=∠2,求证:∠F
=∠G.
2、如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1
+∠2
=
90°
求证:(1)AB∥CD
;
(2)∠2
+∠3
=
90°.
3、如图,在四边形ABCD中,AB∥CD,点E、F分别在AD、BC边上,连结AC交EF于G,∠1=∠BAC.
(1)求证:EF∥CD;
(2)若∠CAF=15°,∠2=45°,∠3=20°,求∠B和∠ACD的度数.
已知,四边形ABCD中,∠A=∠C=90°,E是AB上一点,且∠ADC=∠DEB,
求证:(1)DE//BC;(2)∠EDC=90°
5、阅读理解:
在同一个平面内,两条直线线被第三条直线所截,在截线同旁,且截线之内的两角,叫做同旁内角.如图,∠2和∠6是同旁内角,∠1和∠5是同旁内角.
操作:在平面内画两条平行线,再画一条直线截两条平行线,用量角器观察同
旁内角之间的关系是
.
根据上面结论,回答下面问题:
(1)如图1,MA1∥NA2,则∠A1+∠A2=
度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=
度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=
度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=
度.从上述结论中你发现了什么规律?请在图1,图2,图3,图4中选一个证明你的结论.
(2)如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=
度.
(3)利用上述结论解决问题:如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E
=
140?,求∠BFD的度数.
6、如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t的值.
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM-∠NOC的度数.
【巩固练习】
(一)、填空
1、如图1,已知∠1
=
100°,AB∥CD,则∠2
=______,∠3
=
________,∠4
=________.
2、如图2,直线AB、CD被EF所截,若∠1
=∠2,则∠AEF
+∠CFE
=________.
3、如图3所示
若EF∥AC,则∠A
+∠
_____
=
180°,∠F
+
∠________
=
180°;
(2)若∠2
=∠________,则AE∥BF;
(3)若∠A
+∠________=
180°,则AE∥BF.
4、如图4,AB∥CD,∠2
=
2∠1,则∠2
=________.
(二)、解答题
1、已知:AB∥CD,GM平分∠BGF,HM平分∠DHE.求证:GM⊥HM.
2、已知:AB∥CD,GM平分∠AGF,HN平分∠DHE.求证:GM∥HN.
个性化辅导讲义
—
学生版
授课日期:
学员编号:
年
级:七年级
课
时
数:
学员姓名:
辅导科目:数学
学科教师:
垂直
【学习目标】
1、进一步丰富对两条直线互相平行或垂直的认识,理解平行线、垂线、垂线段的概念;
2、掌握平行线的判定定理与性质定理;
3、培养学生探索精神,发散其思维.
【知识精讲】
一、相交线
1.直线的位置关系
在同一平面内直线与直线的位置关系只有两种:相交和平行.
2.垂线
当两条直角相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
3.垂线的性质
基本事实:过一点有且只有一条直线与已知直线垂直.
4.垂线段最短
直线外一点与直线上各点连接的所有线段中,垂线段最短.
5.点到直线的距离
直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
二、平行线
1.平行公理
基本事实:过直线外一点有且只有一条直线与这条直线平行.
2.平行线的判定
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行.
3.平行线的性质
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补.
【基础练习】
1、判别下列说法是否正确,并说明理由:
⑴不相交的两条直线是平行线;
(
)
⑵在同一平面内,两条不相交的线段是平行线;(
)
⑶过一点可以而且只可以画一条直线与已知直线平行.(
)
⑷同一平面内的3条直线,它们的交点个数可能是0或1或2或3.(
)
⑸在同一平面内,和第三条直线都不相交的2条直线平行.(
)
⑹过2条相交直线外一点A,能作一条直线与这2条直线都平行.(
)
2、在同一平面内,两条不重合的直线的位置关系只有两种:________、________.
3、如图,在正方体中:
⑴找出与线段平行的线段:________________________.
⑵找出与线段垂直的线段:________________________.
4、如图1,OA⊥OB,
∠BOC=300,
OD平分∠AOC,则∠BOD=
5、如图2,OC⊥OD,∠1=35°,则∠2=
°.
6、下列说法错误的是
(
)
A、过
一
点
有
且
只
有
一
条
直
线
与
已
知
直
线
垂
直.
B、过
直
线
外的一
点
有
且
只
有
一条
直
线
与
已
知
直
线
平
行
C、过两点有且只有一条直线
D、两点之间的距离是连接两点的线段
【例题精讲】
]
(一)、选择题
1、对于直线AB,线段CD,射线EF,在下列各图中能相交的是(
)
2、∠A两边分别垂直于∠B的两边,∠A与∠B的关系是
(
)
A、相等
B、互补
C、相等或互补
D、不能确定
3、如图,将一副三角板叠放在一起,使直角顶点重合于点A,
则∠BAE+∠CAD的度数为
(
)
A、120°
B、135°
C、150°
D、180°
4、下列结论正确的有
(
)
A、如果⊥,⊥,那么⊥
B、⊥,∥,那么∥
C、如果∥,⊥,
那么∥
D、如果⊥,∥,那么⊥
(二)、解答题
1、如图,已知∠ABE
+∠DEB
=
180°,∠1
=∠2,求证:∠F
=∠G.
2、如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1
+∠2
=
90°
求证:(1)AB∥CD
;
(2)∠2
+∠3
=
90°.
3、如图,在四边形ABCD中,AB∥CD,点E、F分别在AD、BC边上,连结AC交EF于G,∠1=∠BAC.
(1)求证:EF∥CD;
(2)若∠CAF=15°,∠2=45°,∠3=20°,求∠B和∠ACD的度数.
已知,四边形ABCD中,∠A=∠C=90°,E是AB上一点,且∠ADC=∠DEB,
求证:(1)DE//BC;(2)∠EDC=90°
5、阅读理解:
在同一个平面内,两条直线线被第三条直线所截,在截线同旁,且截线之内的两角,叫做同旁内角.如图,∠2和∠6是同旁内角,∠1和∠5是同旁内角.
操作:在平面内画两条平行线,再画一条直线截两条平行线,用量角器观察同
旁内角之间的关系是
.
根据上面结论,回答下面问题:
(1)如图1,MA1∥NA2,则∠A1+∠A2=
度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=
度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=
度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=
度.从上述结论中你发现了什么规律?请在图1,图2,图3,图4中选一个证明你的结论.
(2)如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=
度.
(3)利用上述结论解决问题:如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E
=
140?,求∠BFD的度数.
6、如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t的值.
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM-∠NOC的度数.
【巩固练习】
(一)、填空
1、如图1,已知∠1
=
100°,AB∥CD,则∠2
=______,∠3
=
________,∠4
=________.
2、如图2,直线AB、CD被EF所截,若∠1
=∠2,则∠AEF
+∠CFE
=________.
3、如图3所示
若EF∥AC,则∠A
+∠
_____
=
180°,∠F
+
∠________
=
180°;
(2)若∠2
=∠________,则AE∥BF;
(3)若∠A
+∠________=
180°,则AE∥BF.
4、如图4,AB∥CD,∠2
=
2∠1,则∠2
=________.
(二)、解答题
1、已知:AB∥CD,GM平分∠BGF,HM平分∠DHE.求证:GM⊥HM.
2、已知:AB∥CD,GM平分∠AGF,HN平分∠DHE.求证:GM∥HN.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
