湘教版数学七年级上册第二章代数式 章末复习 课件(30张ppt)
文档属性
| 名称 | 湘教版数学七年级上册第二章代数式 章末复习 课件(30张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 07:12:50 | ||
图片预览









文档简介
章末复习
湘教版 七年级上册
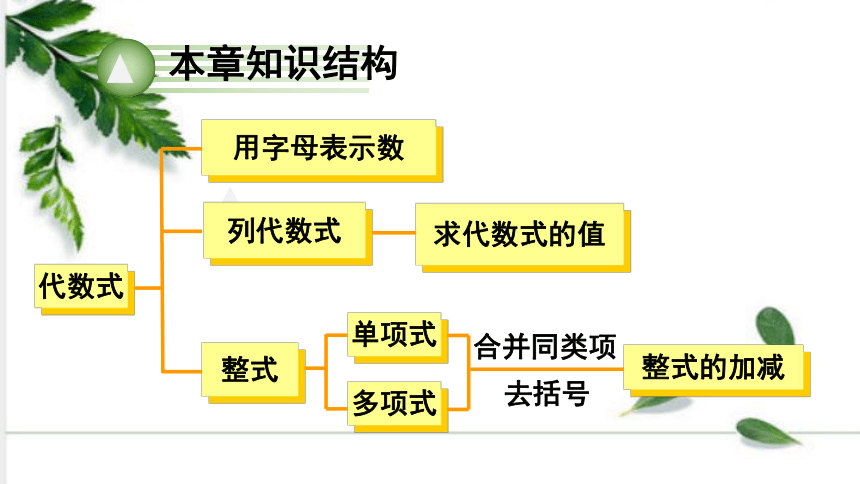
本章知识结构
用字母表示数
列代数式
整式
整式的加减
代数式
求代数式的值
单项式
多项式
合并同类项
去括号
回顾
1.请举出用字母表示数的实例。
已知“天宫一号”大约每小时绕地球飞行2.844万千米,则它飞行th,那么它飞行了2.844t万千米。
2. 什么叫代数式?列代数式时,一般怎么规范书写?如何求代数式的值?
把数与表示数的字母用运算符号连接而成的式子叫做代数式。
用字母表示式子时应注意:
1.在含有字母的式子里,数字和字母,字母和字母中间的乘号可以记作“·”,也可以省略不写。省略乘号时,一般把数字写在字母的前面。
2.两个相同字母相乘时,写成乘方的形式。
3.当数字1与字母相乘时,1也省略不写。
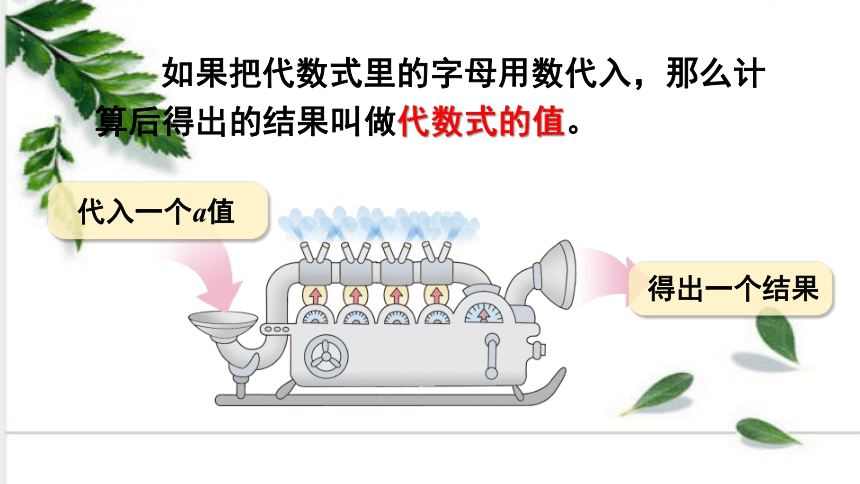
代入一个a值
得出一个结果
如果把代数式里的字母用数代入,那么计算后得出的结果叫做代数式的值。
做一做
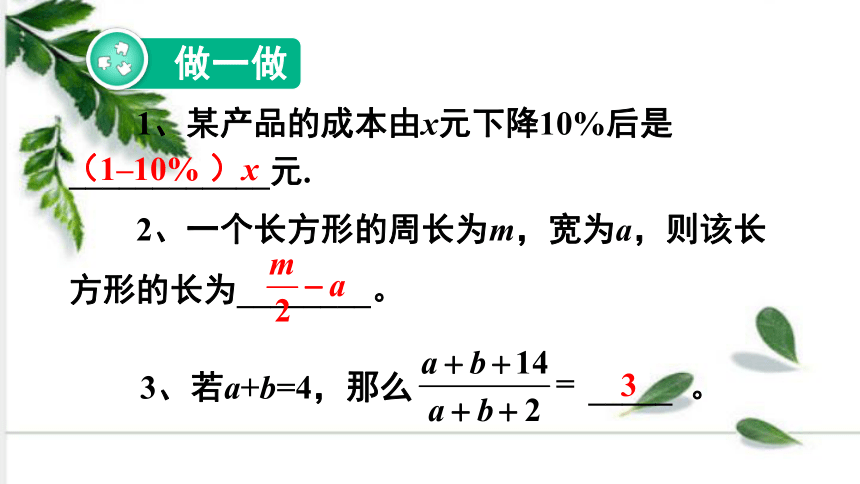
1、某产品的成本由x元下降10%后是____________元.
2、一个长方形的周长为m,宽为a,则该长方形的长为________。
(1–10% )x
3、若a+b=4,那么 _____ 。
3
回顾
3. 什么叫单项式、多项式?单独一个数或字母是单项式吗?单项式的次数、多项式的次数分别是如何确定的?
由数字与字母的积组成的代数式叫做单项式。
由几个单项式的和组成的代数式叫做多项式。
单独一个字母或者一个数也是单项式。
一个单项式中,所有字母的指数的和叫做这个单项式的次数。
多项式中次数最高的项的次数,叫做这个多项式的次数。
做一做
1、在式子: , , , , ,
1–x–5xy2,–x中,哪些是单项式,哪些是多项式?哪些是整式?
单项式有 , ,–x
多项式有 ,1–x–5xy2
整式 , ,–x, , 1–x–5xy2
2、 的系数是( ),次数是( ),
的系数是( ),次数是( )。
1
3、 的项是( ),次数是( ),
1–x–5xy2的项是( ),次数是( ),是( )次( )项式.
2
1
1、–x、–5xy2
3
3
3
回顾
4. 什么叫同类项?怎样合并同类项?
像多项式 xy – 中的项 xy, 这样,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项.
同类项合并过程中,把同类项的系数相加,字母和字母的指数不变。不是同类项不可以合并。
1、下列各组是不是同类项:
做一做
(1)4abc 与 4ab
(2)–5 m2 n3 与 2n3 m2
(3)–0.3 x2 y 与 y x2
不是
是
是
2、合并下列同类项:
(1)3xy – 4 xy – xy = ( )
(2)– a – a – 2a=( )
(3)0.8ab3 – a3 b+0.2ab3 =( )
–2xy
–4a
ab3–a3b
回顾
5、去括号的法则是什么?
括号前是“+”号,运用加法结合律把括号去掉,原括号里各项的符号都不变.
括号前是“–”号,把括号和它前面的
“–”号去掉,原括号里各项的符号都要改变。
1、去括号:(1)+(x-3)=
(2)-(x-3)=
(3)-(x+5y-2)=
(4)+(3x-5y+6z)=
做一做
x–3
– x+3
– x – 5y+2
3x – 5y+6z
2、计算:(1)x-(-y -z+1)=___________;
(2)m+(-n+q)=____________;
(3)a - (b+c-3)=____________;
(4)x+(5-3y)=___________.
x+y +z –1
m-n+q
a-b-c+3
x+5-3y
航行问题
一条河流的水流速度是x千米/秒,已知轮船在静水中的速度是y千米/秒,则轮船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?
解:当船顺水行驶时,船的速度是(x+y)千米/秒,当船逆水行驶时,船的速度是(x–y)千米/秒
船在河流中行驶时,需要分两种情况讨论:
顺水行驶:
船的速度=船在静水中的速度+水流的速度
逆水行驶:
船的速度=船在静水中的速度-水流的速度
典型例题
1.做大小两个长方体纸盒,尺寸如下(单位:cm):
a
b
c
2a
3b
4c
(1)做这两个纸盒共用料多少平方厘米?
解:小纸盒的表面积是:
(2ab+2bc+2ac)cm2
大纸盒的表面积是:
2×2a×3b+2×3b×4c+2×2a×4c
=(12ab+24bc+16ac)cm2
共用料:(2ab+2bc+2ac)+(12ab+24bc+16ac)
= 14ab+26bc+18ac (cm2)
(2)做大纸盒比做小纸盒多用料多少平方厘米?
(12ab+24bc+16ac)–(2ab+2bc+2ac)
= 10ab+22bc+14ac (cm2)
(2)5a2 -[a2+(5 a2 -2a) -2(a2 -3a)]
(1) 3(xy2-x2y) -2(xy+xy2)+3x2y;
2.计算
= 3xy2-3x2y -2xy - 2xy2+3x2y
= xy2 - 2xy
= 5a2 -a2 - 5a2 +2a+2a2 -6a
= a2 - 4a
其中 x = – 1 ,y = 2
3.
解 6xy – [3x2–2(x2–2xy)+1]
= 6xy–3x2+2x2–4xy–1
= –x2+ 2xy –1
当 x = – 1 ,y = 2时,
原式= –(–1)2+2×(–1 )×2–1= –6
4.已知 , ,求 。
解 A+5B =(x+2y)+5(3x–5y)
= x+2y+15x–25y
= 16x–23y
5.观察下列图形中火柴棒的摆放方式。
③
②
①
梯形个数
1
2
3
4
5
火柴棒根数
(1)填写下表 :
5
9
13
17
21
(2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?
4n+1
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢!
湘教版 七年级上册
本章知识结构
用字母表示数
列代数式
整式
整式的加减
代数式
求代数式的值
单项式
多项式
合并同类项
去括号
回顾
1.请举出用字母表示数的实例。
已知“天宫一号”大约每小时绕地球飞行2.844万千米,则它飞行th,那么它飞行了2.844t万千米。
2. 什么叫代数式?列代数式时,一般怎么规范书写?如何求代数式的值?
把数与表示数的字母用运算符号连接而成的式子叫做代数式。
用字母表示式子时应注意:
1.在含有字母的式子里,数字和字母,字母和字母中间的乘号可以记作“·”,也可以省略不写。省略乘号时,一般把数字写在字母的前面。
2.两个相同字母相乘时,写成乘方的形式。
3.当数字1与字母相乘时,1也省略不写。
代入一个a值
得出一个结果
如果把代数式里的字母用数代入,那么计算后得出的结果叫做代数式的值。
做一做
1、某产品的成本由x元下降10%后是____________元.
2、一个长方形的周长为m,宽为a,则该长方形的长为________。
(1–10% )x
3、若a+b=4,那么 _____ 。
3
回顾
3. 什么叫单项式、多项式?单独一个数或字母是单项式吗?单项式的次数、多项式的次数分别是如何确定的?
由数字与字母的积组成的代数式叫做单项式。
由几个单项式的和组成的代数式叫做多项式。
单独一个字母或者一个数也是单项式。
一个单项式中,所有字母的指数的和叫做这个单项式的次数。
多项式中次数最高的项的次数,叫做这个多项式的次数。
做一做
1、在式子: , , , , ,
1–x–5xy2,–x中,哪些是单项式,哪些是多项式?哪些是整式?
单项式有 , ,–x
多项式有 ,1–x–5xy2
整式 , ,–x, , 1–x–5xy2
2、 的系数是( ),次数是( ),
的系数是( ),次数是( )。
1
3、 的项是( ),次数是( ),
1–x–5xy2的项是( ),次数是( ),是( )次( )项式.
2
1
1、–x、–5xy2
3
3
3
回顾
4. 什么叫同类项?怎样合并同类项?
像多项式 xy – 中的项 xy, 这样,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项.
同类项合并过程中,把同类项的系数相加,字母和字母的指数不变。不是同类项不可以合并。
1、下列各组是不是同类项:
做一做
(1)4abc 与 4ab
(2)–5 m2 n3 与 2n3 m2
(3)–0.3 x2 y 与 y x2
不是
是
是
2、合并下列同类项:
(1)3xy – 4 xy – xy = ( )
(2)– a – a – 2a=( )
(3)0.8ab3 – a3 b+0.2ab3 =( )
–2xy
–4a
ab3–a3b
回顾
5、去括号的法则是什么?
括号前是“+”号,运用加法结合律把括号去掉,原括号里各项的符号都不变.
括号前是“–”号,把括号和它前面的
“–”号去掉,原括号里各项的符号都要改变。
1、去括号:(1)+(x-3)=
(2)-(x-3)=
(3)-(x+5y-2)=
(4)+(3x-5y+6z)=
做一做
x–3
– x+3
– x – 5y+2
3x – 5y+6z
2、计算:(1)x-(-y -z+1)=___________;
(2)m+(-n+q)=____________;
(3)a - (b+c-3)=____________;
(4)x+(5-3y)=___________.
x+y +z –1
m-n+q
a-b-c+3
x+5-3y
航行问题
一条河流的水流速度是x千米/秒,已知轮船在静水中的速度是y千米/秒,则轮船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?
解:当船顺水行驶时,船的速度是(x+y)千米/秒,当船逆水行驶时,船的速度是(x–y)千米/秒
船在河流中行驶时,需要分两种情况讨论:
顺水行驶:
船的速度=船在静水中的速度+水流的速度
逆水行驶:
船的速度=船在静水中的速度-水流的速度
典型例题
1.做大小两个长方体纸盒,尺寸如下(单位:cm):
a
b
c
2a
3b
4c
(1)做这两个纸盒共用料多少平方厘米?
解:小纸盒的表面积是:
(2ab+2bc+2ac)cm2
大纸盒的表面积是:
2×2a×3b+2×3b×4c+2×2a×4c
=(12ab+24bc+16ac)cm2
共用料:(2ab+2bc+2ac)+(12ab+24bc+16ac)
= 14ab+26bc+18ac (cm2)
(2)做大纸盒比做小纸盒多用料多少平方厘米?
(12ab+24bc+16ac)–(2ab+2bc+2ac)
= 10ab+22bc+14ac (cm2)
(2)5a2 -[a2+(5 a2 -2a) -2(a2 -3a)]
(1) 3(xy2-x2y) -2(xy+xy2)+3x2y;
2.计算
= 3xy2-3x2y -2xy - 2xy2+3x2y
= xy2 - 2xy
= 5a2 -a2 - 5a2 +2a+2a2 -6a
= a2 - 4a
其中 x = – 1 ,y = 2
3.
解 6xy – [3x2–2(x2–2xy)+1]
= 6xy–3x2+2x2–4xy–1
= –x2+ 2xy –1
当 x = – 1 ,y = 2时,
原式= –(–1)2+2×(–1 )×2–1= –6
4.已知 , ,求 。
解 A+5B =(x+2y)+5(3x–5y)
= x+2y+15x–25y
= 16x–23y
5.观察下列图形中火柴棒的摆放方式。
③
②
①
梯形个数
1
2
3
4
5
火柴棒根数
(1)填写下表 :
5
9
13
17
21
(2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?
4n+1
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢!
同课章节目录
