湘教版数学七年级上册第四章 图形的认识 章末复习 课件(21张ppt)
文档属性
| 名称 | 湘教版数学七年级上册第四章 图形的认识 章末复习 课件(21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 00:00:00 | ||
图片预览







文档简介
章末复习
湘教版七年级上册
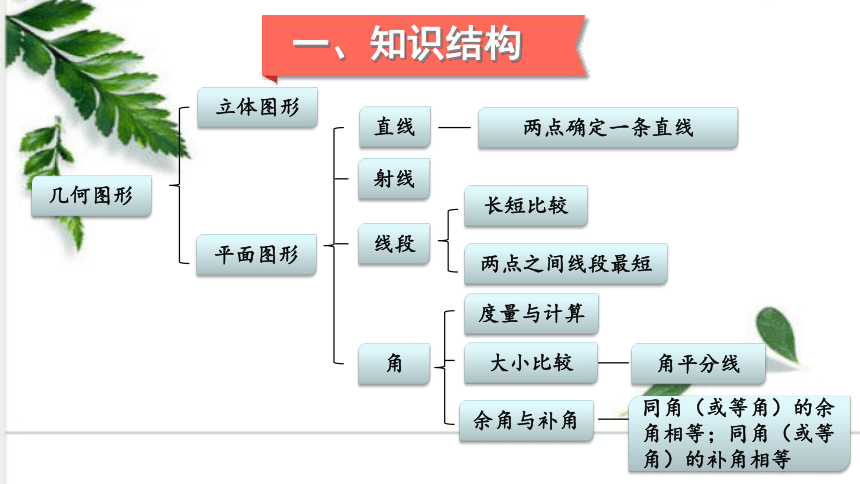
一、知识结构
几何图形
立体图形
平面图形
直线
两点确定一条直线
射线
线段
角
长短比较
两点之间线段最短
度量与计算
大小比较
角平分线
余角与补角
同角(或等角)的余角相等;同角(或等角)的补角相等
二、释疑解惑,加深理解
1.立体图形的概念:
各部分不在同一平面内的几何图形叫做立体图形.
2.平面图形的概念:
各部分都在同一平面内的几何图形是平面图形.
3.线段、射线、直线的区别:
线段有两个端点.射线有一个端点.直线没有端点.
4.线段、直线的相关定理:
过两点又且只有一条直线.简称两点确定一条直线.
两点之间的所有连线中,线段最短.简称“两点之间线段最短”.
5.角的概念:
我们把一条射线绕着它的端点从一个位置旋转到另外一个位置时所成的图形叫做角.
6.角的大小比较方法:
①度量法;②叠合法.
7.角平分线的概念:
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,那么这条射线叫做这个角的平分线.
8.角的度数之间的换算率:
1°=60′ 1′=60″
1′=( )° 1″=( )′
9.余角的概念:
如果两个角的和是90°,那么这两个角互为余角,其中一个角是另一个角的余角.
10.补角的概念:
如果两个角的和是180°,那么这两个角互为补角,其中一个角是另一个角的补角.
11.余角、补角的相关定理:
同角(或等角)的补角相等.同角(或等角)的余角相等.
三、典例精析,复习旧知
1.下列说法中,正确的有( )
(1)过两点有且只有一条线段;
(2)连结两点的线段叫做两点的距离;
(3)两点之间,线段最短;
(4)AB=BC,则点B是线段AC的中点;
(5)射线比直线短.
A.1个 B.2个 C.3个 D.4个
C
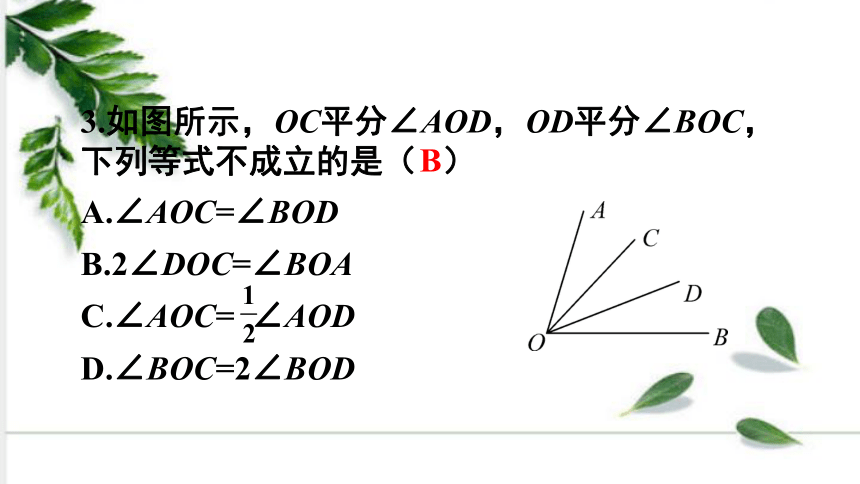
3.如图所示,OC平分∠AOD,OD平分∠BOC,下列等式不成立的是( )
A.∠AOC=∠BOD
B.2∠DOC=∠BOA
C.∠AOC= ∠AOD
D.∠BOC=2∠BOD
B
4.下列说法正确的是( )
A.直线AB和直线BA是两条直线;
B.射线AB和射线BA是两条射线;
C.线段AB和线段BA是两条线段;
D.直线AB和直线a不能是同一条直线.
B
5.如果∠α+∠β=90°,而∠β与∠γ互余,那么∠α与∠γ的关系为( )
A.互余 B.互补
C.相等 D.不能确定.
C
6.下列说法中错误的有( )
(1)线段有两个端点,直线有一个端点;
(2)角的大小与我们画出的角的两边的长短无关;
(3)线段上有无数个点;
(4)同角或等角的补角相等;
(5)两个锐角的和一定大于直角
A.1个 B.2个
C.3个 D.4个
B
7.如下图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG和∠BGM的大小.
答案:∠DEG=100°,
∠BGM=80°
8.如图所示,AD= DB,E是BC的中点,
BE= AC=2cm,求线段DE的长.
因为E是BC的中点,
所以BE=EC=2cm,BC=2BE=4cm,
又因为AC=5BE=10cm.
所以AB=AC-BC=10-4=6cm,
且AB=AD+BD=AD+2AD=3AD,
所以AD=2cm,BD=4cm,
DE=DB+BE=4+2=6cm.
7.直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
答案:∠2=100°;
∠3=180°-∠FOC-∠1=50°
8.已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,并求出图中线段的条数;
(2)若图中所有线段的长度和为26,求线段AC的长度;
(3)若E为线段BC上的点,M为EB的中点,DM=a,CE=b,求线段AB的长度.
解:(1)线段一共有6条.
(2)设AD=x,
则DC=x,CB=2x,AC=2x,DB=3x,AB=4x,
∴AD+AC+AB+DC+DB+CB=13x.
∴13x=26 ∴x=2 ∴AC=4.
(3)AB=AC+CE+BE
=2DC+CE+2EM
=2(DC+EM)+CE
=2(a-b)+b=2a-b.
A
C
B
D
E
M
通过本节课的学习,你有哪些收获?
还存在哪些疑惑?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢!
湘教版七年级上册
一、知识结构
几何图形
立体图形
平面图形
直线
两点确定一条直线
射线
线段
角
长短比较
两点之间线段最短
度量与计算
大小比较
角平分线
余角与补角
同角(或等角)的余角相等;同角(或等角)的补角相等
二、释疑解惑,加深理解
1.立体图形的概念:
各部分不在同一平面内的几何图形叫做立体图形.
2.平面图形的概念:
各部分都在同一平面内的几何图形是平面图形.
3.线段、射线、直线的区别:
线段有两个端点.射线有一个端点.直线没有端点.
4.线段、直线的相关定理:
过两点又且只有一条直线.简称两点确定一条直线.
两点之间的所有连线中,线段最短.简称“两点之间线段最短”.
5.角的概念:
我们把一条射线绕着它的端点从一个位置旋转到另外一个位置时所成的图形叫做角.
6.角的大小比较方法:
①度量法;②叠合法.
7.角平分线的概念:
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,那么这条射线叫做这个角的平分线.
8.角的度数之间的换算率:
1°=60′ 1′=60″
1′=( )° 1″=( )′
9.余角的概念:
如果两个角的和是90°,那么这两个角互为余角,其中一个角是另一个角的余角.
10.补角的概念:
如果两个角的和是180°,那么这两个角互为补角,其中一个角是另一个角的补角.
11.余角、补角的相关定理:
同角(或等角)的补角相等.同角(或等角)的余角相等.
三、典例精析,复习旧知
1.下列说法中,正确的有( )
(1)过两点有且只有一条线段;
(2)连结两点的线段叫做两点的距离;
(3)两点之间,线段最短;
(4)AB=BC,则点B是线段AC的中点;
(5)射线比直线短.
A.1个 B.2个 C.3个 D.4个
C
3.如图所示,OC平分∠AOD,OD平分∠BOC,下列等式不成立的是( )
A.∠AOC=∠BOD
B.2∠DOC=∠BOA
C.∠AOC= ∠AOD
D.∠BOC=2∠BOD
B
4.下列说法正确的是( )
A.直线AB和直线BA是两条直线;
B.射线AB和射线BA是两条射线;
C.线段AB和线段BA是两条线段;
D.直线AB和直线a不能是同一条直线.
B
5.如果∠α+∠β=90°,而∠β与∠γ互余,那么∠α与∠γ的关系为( )
A.互余 B.互补
C.相等 D.不能确定.
C
6.下列说法中错误的有( )
(1)线段有两个端点,直线有一个端点;
(2)角的大小与我们画出的角的两边的长短无关;
(3)线段上有无数个点;
(4)同角或等角的补角相等;
(5)两个锐角的和一定大于直角
A.1个 B.2个
C.3个 D.4个
B
7.如下图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG和∠BGM的大小.
答案:∠DEG=100°,
∠BGM=80°
8.如图所示,AD= DB,E是BC的中点,
BE= AC=2cm,求线段DE的长.
因为E是BC的中点,
所以BE=EC=2cm,BC=2BE=4cm,
又因为AC=5BE=10cm.
所以AB=AC-BC=10-4=6cm,
且AB=AD+BD=AD+2AD=3AD,
所以AD=2cm,BD=4cm,
DE=DB+BE=4+2=6cm.
7.直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
答案:∠2=100°;
∠3=180°-∠FOC-∠1=50°
8.已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,并求出图中线段的条数;
(2)若图中所有线段的长度和为26,求线段AC的长度;
(3)若E为线段BC上的点,M为EB的中点,DM=a,CE=b,求线段AB的长度.
解:(1)线段一共有6条.
(2)设AD=x,
则DC=x,CB=2x,AC=2x,DB=3x,AB=4x,
∴AD+AC+AB+DC+DB+CB=13x.
∴13x=26 ∴x=2 ∴AC=4.
(3)AB=AC+CE+BE
=2DC+CE+2EM
=2(DC+EM)+CE
=2(a-b)+b=2a-b.
A
C
B
D
E
M
通过本节课的学习,你有哪些收获?
还存在哪些疑惑?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢!
同课章节目录
