苏科版九年级下册数学 5.4二次函数和一元二次方程课件(共22张PPT)
文档属性
| 名称 | 苏科版九年级下册数学 5.4二次函数和一元二次方程课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
5.4.2二次函数
与一元二次方程
九年级(下册)
初中数学
抛物线y=ax2+bx+c与x轴有两个公共点
一、抛物线y=ax2+bx+c与x轴的交点个数
可由b2-4ac的符号决定。
二、抛物线y=ax2+bx+c与x轴的交点的横坐标
是一元二次方程ax2+bx+c=0的根。
抛物线y=ax2+bx+c与x轴有唯一公共点
抛物线y=ax2+bx+c与x轴没有公共点
(1)b2-4ac>0
(2)b2-4ac
=0
(3)b2-4ac
<0
知识回顾
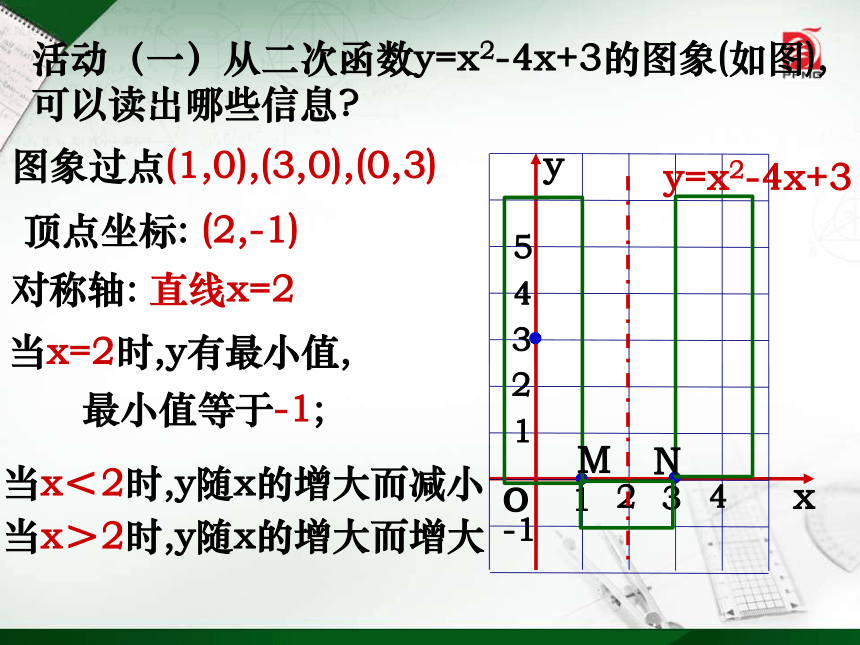
活动(一)从二次函数y=x2-4x+3的图象(如图),可以读出哪些信息?
y=x2-4x+3
M
N
图象过点(1,0),(3,0),(0,3)
当x=2时,y有最小值,
最小值等于-1;
当x<2时,y随x的增大而减小
当x>2时,y随x的增大而增大
顶点坐标:
(2,-1)
对称轴:
直线x=2
y=x2-4x+3
M
N
当x<1或x>3时,
y>0
即:x2-4x+3>0
当1<x<3时,
y<0
即:x2-4x+3<0
(x轴上方的图象)
(x轴下方的图象)
数形结合思想
从二次函数y=x2-4x+3的图象(如图),可以读出哪些信息?
长春版小学语文三年级下课后词语拼音填词语
1
1-1
h
ón
g
t
óng
t
óng
h
ēi
y
ā
y
ā
ch
én
di
ān
di
ān
ru
ǎn
mi
án
mi
án
(
)(
)
(
)
(
)
q
īn
g
pi
āo
pi
āo
gu
āng
?
t
ū
t
ū
m
íng
hu
ǎng
?
hu
ǎng
?
j
ìn
g
qi
āo
qi
āo
(
)(
)(
)
(
)
h
àn
l
ín
l
ín
y
ā
l
ì
y
à
b
ǎn
sh
ān
qi
ū
li
án
mi
án
ān
j
ìn
g
(
)
(
)(
)
(
)(
)
(
)
l
ín
y
ǔ
g
u
à
ni
àn
ji
ǎng
?
p
ǐn
hu
ǎng
?
y
ǎn
t
ón
g
y
ún
hu
àng
?
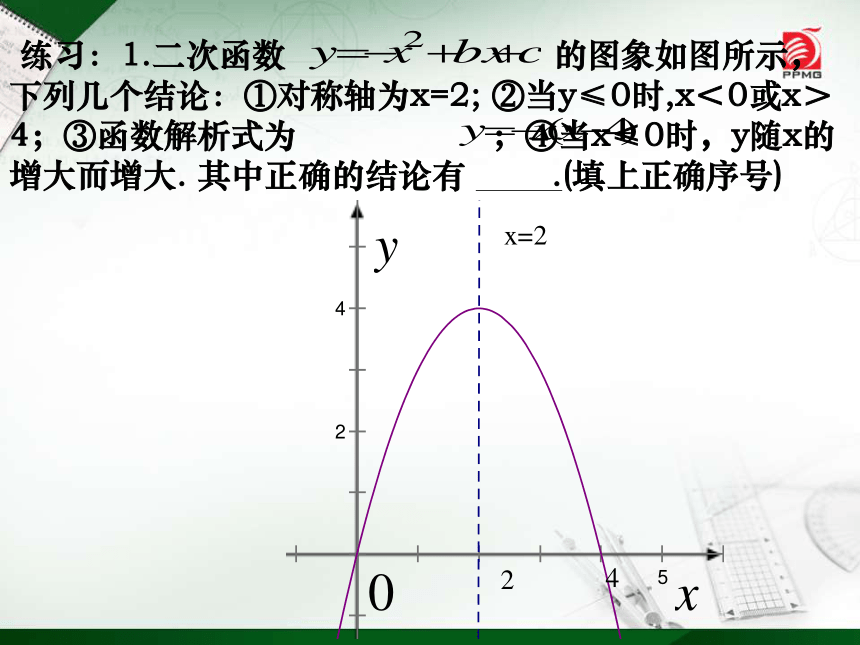
练习:1.二次函数
的图象如图所示,下列几个结论:①对称轴为x=2;
②当y≤0时,x<0或x>4;③函数解析式为
;④当x≤0时,y随x的增大而增大.
其中正确的结论有
.(填上正确序号)
练习:2.如图所示的抛物线:
当x=_________.时,y=0;
当x<-2或x>0时,
y_________0;
当x在____________范围内时,y≥0;
当x=________时,y有最大值_____.
<
-2或0
-2≤x≤0
-1
3
练习:
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,
根据图象解答下列问题.
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个
不相等的实数根,求k的取值范围.
x=1或x=3
1<x<3
x
>
2
k
<
2
1.已知:抛物线y=ax2+bx+c,当x=-1时有最大值,若x=-5,-2,1时对应的函数值分别为y1、y2、y3,则y1、y2、y3的大小关系为
(
)
A.y1<y2<y3
B.y1>y2>y3
C.y1>y3>
y2
D.y2>y3
>y1
D
例题分析:
x=-1
(-2,y2)
(1,y3)
(-5,y1)
数形结合思想
(-3,y3)
-1
y
O
x
P1
P2
P3
1.已知抛物线和直线在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),
P2(x2,y2)是抛物线上的点,
P3(x3,y3)是直线上的点
,
且-1<
x1
则比较y1
,y2
,y3的大小.
y2<
y1
练习:
y2
练习:
2.如图,已知:抛物线y1=ax2+bx+c与直线y2=kx+m相交于A(5,3)和B(2,-1).
则当x满足条件
时,y1=y2;
则当x满足条件
时,y1>y2;
x
A(5,3)
(2,-1)B
y1
X=2或x=5
则当x满足条件
时,y1
≤y2;
x<2或x>5
2≤x
≤
5
活动(二)已知二次函数y=x2+2x-5的图像
你能探索方程x2+2x-5=0的根的取值范围吗?
y=x2+2x-5
问题1.观察图象,抛物线与
x轴有两个公共点,说出他们横坐标分别在什么整数范围内?
-4<x1<-3,
1<x2<2
(x1,0)
(x2,0)
则一元二次方程的两个根就在-4与-3,1与2之间
这两个根分别是1.5和-3.5吗?
探索:利用二次函数y=x2+2x-5的图像,
求方程x2+2x-5=0的近似根.
问题2.观察图象并借助于计算,你能探索x1与x2的
近似值?(精确到0.1)
(x1,0)
(x2,0)
以右边的交点为例
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
1.进一步缩小范围,
1.5
0.25
>0
当X=1.5时,y=0.25
>0.说明使y=0的x的值一定在1与1.5之间,即1
<x
<1.5
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
2.进一步缩小范围,
1.5
0.25
>0
当x=1.25时,y=-0.9375
<
0.说明使y=0的x的值一定在1.25与1.5之间,即1.25
<x
<1.5
1.25
-0.9375
<0
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
3.进一步缩小范围,
1.5
0.25
>0
当x=1.3时,y=-0.
71
<
0.说明使y=0的x的值一定在1.3与1.5之间,即1.3
<x
<1.5
1.25
-0.9375
<0
1.3
-0.71
<0
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
4.进一步缩小范围,
1.5
0.25
>0
当x=1.4时,y=-0.
24
<
0.说明使y=0的x的值一定在1.4与1.5之间,即1.4
<x
<1.5
1.25
-0.9375
<0
1.3
-0.71
<0
1.4
-0.24
<0
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
5.
缩小范围到1.4
<x
<1.5,由于要精确到
0.1,必须运算到0.01.
1.5
0.25
>0
1.25
-0.9375
<0
1.3
-0.71
<0
1.4
-0.24
<0
1.45
0.0025
>0
则1.40
<x
<1.45∴使y=0的近似值为1.4
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
问题2.观察图象并借助于计算,你能探索x1与x2的
近似值?(精确到0.1)
(x1,0)
(x2,0)
以右边的交点为例
由上可得,方程x2+2x-5=0
介于1与2之间的根x2的近似值为1.4(精确到0.1)
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
问题3.你能用同样的方法确定方程x2+2x-5=0的另一个根x1(精确到0.1)
(x1,0)
(x2,0)
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
根据上表中二次函数y=ax2+bx+c的自变量x
与函数值y的对应值,判断方程
ax2+bx+c=0(a≠0,
a,b,c为常数)的一个解x的范围是
(
)
A.6<x<6.17
B.
B.
6.17<x<6.18
C.
6.18<x<6.19
D.
6.19<x<6.20
C
尝试练习
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
-0.03
-0.01
0.02
0.04
这节课的收获是……
5.4.2二次函数
与一元二次方程
九年级(下册)
初中数学
抛物线y=ax2+bx+c与x轴有两个公共点
一、抛物线y=ax2+bx+c与x轴的交点个数
可由b2-4ac的符号决定。
二、抛物线y=ax2+bx+c与x轴的交点的横坐标
是一元二次方程ax2+bx+c=0的根。
抛物线y=ax2+bx+c与x轴有唯一公共点
抛物线y=ax2+bx+c与x轴没有公共点
(1)b2-4ac>0
(2)b2-4ac
=0
(3)b2-4ac
<0
知识回顾
活动(一)从二次函数y=x2-4x+3的图象(如图),可以读出哪些信息?
y=x2-4x+3
M
N
图象过点(1,0),(3,0),(0,3)
当x=2时,y有最小值,
最小值等于-1;
当x<2时,y随x的增大而减小
当x>2时,y随x的增大而增大
顶点坐标:
(2,-1)
对称轴:
直线x=2
y=x2-4x+3
M
N
当x<1或x>3时,
y>0
即:x2-4x+3>0
当1<x<3时,
y<0
即:x2-4x+3<0
(x轴上方的图象)
(x轴下方的图象)
数形结合思想
从二次函数y=x2-4x+3的图象(如图),可以读出哪些信息?
长春版小学语文三年级下课后词语拼音填词语
1
1-1
h
ón
g
t
óng
t
óng
h
ēi
y
ā
y
ā
ch
én
di
ān
di
ān
ru
ǎn
mi
án
mi
án
(
)(
)
(
)
(
)
q
īn
g
pi
āo
pi
āo
gu
āng
?
t
ū
t
ū
m
íng
hu
ǎng
?
hu
ǎng
?
j
ìn
g
qi
āo
qi
āo
(
)(
)(
)
(
)
h
àn
l
ín
l
ín
y
ā
l
ì
y
à
b
ǎn
sh
ān
qi
ū
li
án
mi
án
ān
j
ìn
g
(
)
(
)(
)
(
)(
)
(
)
l
ín
y
ǔ
g
u
à
ni
àn
ji
ǎng
?
p
ǐn
hu
ǎng
?
y
ǎn
t
ón
g
y
ún
hu
àng
?
练习:1.二次函数
的图象如图所示,下列几个结论:①对称轴为x=2;
②当y≤0时,x<0或x>4;③函数解析式为
;④当x≤0时,y随x的增大而增大.
其中正确的结论有
.(填上正确序号)
练习:2.如图所示的抛物线:
当x=_________.时,y=0;
当x<-2或x>0时,
y_________0;
当x在____________范围内时,y≥0;
当x=________时,y有最大值_____.
<
-2或0
-2≤x≤0
-1
3
练习:
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,
根据图象解答下列问题.
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个
不相等的实数根,求k的取值范围.
x=1或x=3
1<x<3
x
>
2
k
<
2
1.已知:抛物线y=ax2+bx+c,当x=-1时有最大值,若x=-5,-2,1时对应的函数值分别为y1、y2、y3,则y1、y2、y3的大小关系为
(
)
A.y1<y2<y3
B.y1>y2>y3
C.y1>y3>
y2
D.y2>y3
>y1
D
例题分析:
x=-1
(-2,y2)
(1,y3)
(-5,y1)
数形结合思想
(-3,y3)
-1
y
O
x
P1
P2
P3
1.已知抛物线和直线在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),
P2(x2,y2)是抛物线上的点,
P3(x3,y3)是直线上的点
,
且-1<
x1
,y2
,y3的大小.
y2<
y1
y2
练习:
2.如图,已知:抛物线y1=ax2+bx+c与直线y2=kx+m相交于A(5,3)和B(2,-1).
则当x满足条件
时,y1=y2;
则当x满足条件
时,y1>y2;
x
A(5,3)
(2,-1)B
y1
X=2或x=5
则当x满足条件
时,y1
≤y2;
x<2或x>5
2≤x
≤
5
活动(二)已知二次函数y=x2+2x-5的图像
你能探索方程x2+2x-5=0的根的取值范围吗?
y=x2+2x-5
问题1.观察图象,抛物线与
x轴有两个公共点,说出他们横坐标分别在什么整数范围内?
-4<x1<-3,
1<x2<2
(x1,0)
(x2,0)
则一元二次方程的两个根就在-4与-3,1与2之间
这两个根分别是1.5和-3.5吗?
探索:利用二次函数y=x2+2x-5的图像,
求方程x2+2x-5=0的近似根.
问题2.观察图象并借助于计算,你能探索x1与x2的
近似值?(精确到0.1)
(x1,0)
(x2,0)
以右边的交点为例
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
1.进一步缩小范围,
1.5
0.25
>0
当X=1.5时,y=0.25
>0.说明使y=0的x的值一定在1与1.5之间,即1
<x
<1.5
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
2.进一步缩小范围,
1.5
0.25
>0
当x=1.25时,y=-0.9375
<
0.说明使y=0的x的值一定在1.25与1.5之间,即1.25
<x
<1.5
1.25
-0.9375
<0
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
3.进一步缩小范围,
1.5
0.25
>0
当x=1.3时,y=-0.
71
<
0.说明使y=0的x的值一定在1.3与1.5之间,即1.3
<x
<1.5
1.25
-0.9375
<0
1.3
-0.71
<0
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
4.进一步缩小范围,
1.5
0.25
>0
当x=1.4时,y=-0.
24
<
0.说明使y=0的x的值一定在1.4与1.5之间,即1.4
<x
<1.5
1.25
-0.9375
<0
1.3
-0.71
<0
1.4
-0.24
<0
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
5.
缩小范围到1.4
<x
<1.5,由于要精确到
0.1,必须运算到0.01.
1.5
0.25
>0
1.25
-0.9375
<0
1.3
-0.71
<0
1.4
-0.24
<0
1.45
0.0025
>0
则1.40
<x
<1.45∴使y=0的近似值为1.4
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
x
1
2
y
-2
<0
3
>0
问题2.观察图象并借助于计算,你能探索x1与x2的
近似值?(精确到0.1)
(x1,0)
(x2,0)
以右边的交点为例
由上可得,方程x2+2x-5=0
介于1与2之间的根x2的近似值为1.4(精确到0.1)
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
问题3.你能用同样的方法确定方程x2+2x-5=0的另一个根x1(精确到0.1)
(x1,0)
(x2,0)
探索:利用二次函数y=x2+2x-5的图象,
求方程x2+2x-5=0的近似根.
根据上表中二次函数y=ax2+bx+c的自变量x
与函数值y的对应值,判断方程
ax2+bx+c=0(a≠0,
a,b,c为常数)的一个解x的范围是
(
)
A.6<x<6.17
B.
B.
6.17<x<6.18
C.
6.18<x<6.19
D.
6.19<x<6.20
C
尝试练习
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
-0.03
-0.01
0.02
0.04
这节课的收获是……
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
