第二章 直角三角形的边角关系专项训练 直角三角形的应用(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系专项训练 直角三角形的应用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 09:34:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练 直角三角形的应用
1.(2019·杭州)如图所示,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在
同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A aainx +bsinx B. acosx+bcosx C. asinx+bcosx D. acosx+bsinx
第1题图 第2题图
2(2019·重庆)为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动,如图所示,在一个坡度(或坡比)1=1:2.4的山坡AB上发现有一棵古树CD,测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高约为(参考数据;sin48?≈0.73,cos48?≈0.67,tan48?≈1.11)( )
17.0米 B. 21.9米 C. 23.3米 D. 33.3米
3.(2018·巴彦淖尔)南沙群岛是我国固有领土,现在我南海渔民要在南沙某北海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我国A处的渔监船前往C处护航,如图所示,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为( )
A. 10海里 B. 20海里 C. 20海里 D.10海里
第3题图 第4题图
4.(2018·苏州)如图所示,某海监船以20海里/小时的速度在某海域进行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20海里 D. 40海里
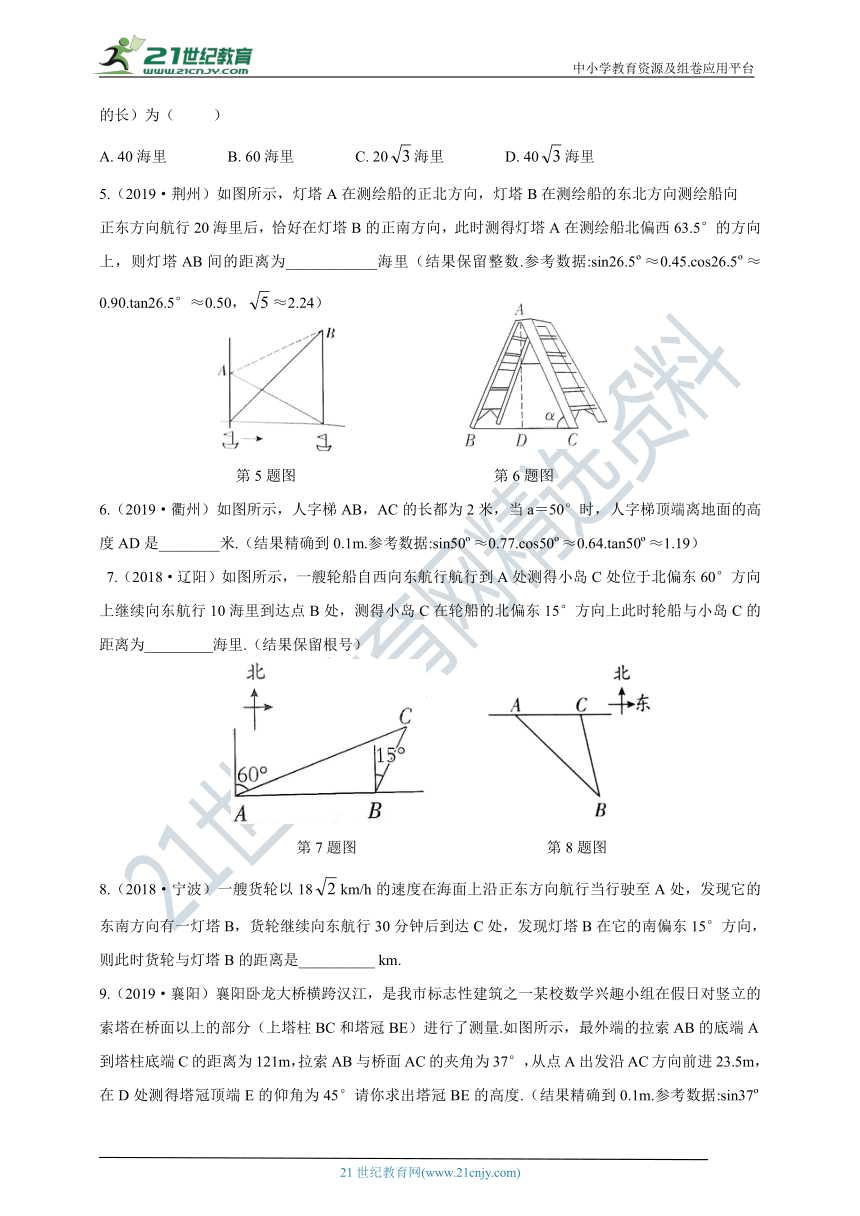
5.(2019·荆州)如图所示,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向测绘船向
正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔AB间的距离为____________海里(结果保留整数.参考数据:sin26.5?≈0.45.cos26.5?≈0.90.tan26.5°≈0.50,≈2.24)
第5题图 第6题图
6.(2019·衢州)如图所示,人字梯AB,AC的长都为2米,当a=50°时,人字梯顶端离地面的高度AD是________米.(结果精确到0.1m.参考数据:sin50?≈0.77.cos50?≈0.64.tan50?≈1.19)
7.(2018·辽阳)如图所示,一艘轮船自西向东航行航行到A处测得小岛C处位于北偏东60°方向上继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上此时轮船与小岛C的距离为_________海里.(结果保留根号)
第7题图 第8题图
8.(2018·宁波)一艘货轮以18km/h的速度在海面上沿正东方向航行当行驶至A处,发现它的东南方向有一灯塔B,货轮继续向东航行30分钟后到达C处,发现灯塔B在它的南偏东15°方向,则此时货轮与灯塔B的距离是__________ km.
9.(2019·襄阳)襄阳卧龙大桥横跨汉江,是我市标志性建筑之一某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°请你求出塔冠BE的高度.(结果精确到0.1m.参考数据:sin37?≈0.60,cos37?≈0.80,tan37?≈0.75,≈1.41)
10.(2019·随州)在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里。
(1)求收到求救讯息时事故渔船P与救助船B之间的距离;
(2)若救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船P
处搜救,试通过计算判断哪艘船先到达.
11.(2019·本溪)小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图1,2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,点B,F在AC上,点C在DE上,支杆DF=30 cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°。请根据以上信息,解决下列问题。
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号)
12.(2019·上海)图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D到BC的距离;
(2)求E,E'两点的距离.
参考答案
D 2. C 3. A 4. D
22 6. 1.5 7. 5 8. 18
9.解:在Rt△ABC中,tanA=,则BC=AC·tanA≈121×0.75=90.75(m)。
由题意得,CD=AC-AD=97.5(m),在Rt△ECD中,∠EDC=45°∴EC=CD=97.5(m)
∴BE=EC-BC=6.75≈6.8(m),
答:塔冠BE的高度约为6.8m.
10.解:(1)如图所示,作PC⊥AB于点C,则∠PCA=∠PCB=90°
由题意得,PA=120(海里),∠A=30°∠BPC=45°,
∴PB=PC=60(海里)
答:收到求救讯息时事故渔船P与救助船B之间的距离为60海里;
(2)∵PA=120海里,PB=60海里,救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,∴救助船A所用的时间为120÷40=3(小时),
救助船B所用的时间为(小时),
∵3>2,∴救助船B先到达.
11,解:(1)如图所示,过点F作FH⊥DE于点H,∴∠FHC=∠FHD=90?。
∵∠FDC=30?,DF=30(cm),∴FH=DF=15(cm), DH=DF=15(cm).
∵∠FCH=45?,∴CH=FH=15(cm).∴CD=CH+ DH=15+15(cm).
∵CE: CD=1:3,∴DE=CD=(20+20) cm.
∵AB=BC=DE,∴AC=(40+40)cm;
(2)如图所示,过点A作AG⊥ED交ED的延长线于点G.
∵∠ACG=45°,∴AG=AC=(20+20)cm.
答:拉杆端点A到水平滑杆ED的距离为(20+20)cm.
12,解:(1)如图所示,过点D'作D'H⊥BC,垂足为点H,交AD于点F.
由题意得, AD'=AD=90 (厘米),∠DAD'=60°.
∴四边形ABCD是矩形,∴AD//BC.∴∠AFD'=∠BHD'=90?。
在Rt△ADF中, D'F=AD'·sin∠DAD'=90×sin60°=45 (厘米).
又∵CE=40(厘米), DE=30(厘米),∴FH=DC=DE+CE=70(厘米).
∴D'H=D'F+FH=(45+70)厘米.
答:点D'到BC的距离为(45+70)厘米;
(2)如图所示,连接AE,AE', EE'.
由题意得,AE'=AE,∠EAE'=60?,∴△AEE'是等边三角形.
∴EE'=AE.∵四边形ABCD是矩形,∴∠ADE=90°。
在Rt△ADE中,AD=90(厘米),DE=30(厘米)。
∴AE==(厘米),∴EE=30(厘米)。
答:E,E'两点的距离为30厘米。
_21?????????è?????(www.21cnjy.com)_
专项训练 直角三角形的应用
1.(2019·杭州)如图所示,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在
同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A aainx +bsinx B. acosx+bcosx C. asinx+bcosx D. acosx+bsinx
第1题图 第2题图
2(2019·重庆)为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动,如图所示,在一个坡度(或坡比)1=1:2.4的山坡AB上发现有一棵古树CD,测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高约为(参考数据;sin48?≈0.73,cos48?≈0.67,tan48?≈1.11)( )
17.0米 B. 21.9米 C. 23.3米 D. 33.3米
3.(2018·巴彦淖尔)南沙群岛是我国固有领土,现在我南海渔民要在南沙某北海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我国A处的渔监船前往C处护航,如图所示,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为( )
A. 10海里 B. 20海里 C. 20海里 D.10海里
第3题图 第4题图
4.(2018·苏州)如图所示,某海监船以20海里/小时的速度在某海域进行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20海里 D. 40海里
5.(2019·荆州)如图所示,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向测绘船向
正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔AB间的距离为____________海里(结果保留整数.参考数据:sin26.5?≈0.45.cos26.5?≈0.90.tan26.5°≈0.50,≈2.24)
第5题图 第6题图
6.(2019·衢州)如图所示,人字梯AB,AC的长都为2米,当a=50°时,人字梯顶端离地面的高度AD是________米.(结果精确到0.1m.参考数据:sin50?≈0.77.cos50?≈0.64.tan50?≈1.19)
7.(2018·辽阳)如图所示,一艘轮船自西向东航行航行到A处测得小岛C处位于北偏东60°方向上继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上此时轮船与小岛C的距离为_________海里.(结果保留根号)
第7题图 第8题图
8.(2018·宁波)一艘货轮以18km/h的速度在海面上沿正东方向航行当行驶至A处,发现它的东南方向有一灯塔B,货轮继续向东航行30分钟后到达C处,发现灯塔B在它的南偏东15°方向,则此时货轮与灯塔B的距离是__________ km.
9.(2019·襄阳)襄阳卧龙大桥横跨汉江,是我市标志性建筑之一某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°请你求出塔冠BE的高度.(结果精确到0.1m.参考数据:sin37?≈0.60,cos37?≈0.80,tan37?≈0.75,≈1.41)
10.(2019·随州)在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里。
(1)求收到求救讯息时事故渔船P与救助船B之间的距离;
(2)若救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船P
处搜救,试通过计算判断哪艘船先到达.
11.(2019·本溪)小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图1,2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,点B,F在AC上,点C在DE上,支杆DF=30 cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°。请根据以上信息,解决下列问题。
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号)
12.(2019·上海)图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D到BC的距离;
(2)求E,E'两点的距离.
参考答案
D 2. C 3. A 4. D
22 6. 1.5 7. 5 8. 18
9.解:在Rt△ABC中,tanA=,则BC=AC·tanA≈121×0.75=90.75(m)。
由题意得,CD=AC-AD=97.5(m),在Rt△ECD中,∠EDC=45°∴EC=CD=97.5(m)
∴BE=EC-BC=6.75≈6.8(m),
答:塔冠BE的高度约为6.8m.
10.解:(1)如图所示,作PC⊥AB于点C,则∠PCA=∠PCB=90°
由题意得,PA=120(海里),∠A=30°∠BPC=45°,
∴PB=PC=60(海里)
答:收到求救讯息时事故渔船P与救助船B之间的距离为60海里;
(2)∵PA=120海里,PB=60海里,救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,∴救助船A所用的时间为120÷40=3(小时),
救助船B所用的时间为(小时),
∵3>2,∴救助船B先到达.
11,解:(1)如图所示,过点F作FH⊥DE于点H,∴∠FHC=∠FHD=90?。
∵∠FDC=30?,DF=30(cm),∴FH=DF=15(cm), DH=DF=15(cm).
∵∠FCH=45?,∴CH=FH=15(cm).∴CD=CH+ DH=15+15(cm).
∵CE: CD=1:3,∴DE=CD=(20+20) cm.
∵AB=BC=DE,∴AC=(40+40)cm;
(2)如图所示,过点A作AG⊥ED交ED的延长线于点G.
∵∠ACG=45°,∴AG=AC=(20+20)cm.
答:拉杆端点A到水平滑杆ED的距离为(20+20)cm.
12,解:(1)如图所示,过点D'作D'H⊥BC,垂足为点H,交AD于点F.
由题意得, AD'=AD=90 (厘米),∠DAD'=60°.
∴四边形ABCD是矩形,∴AD//BC.∴∠AFD'=∠BHD'=90?。
在Rt△ADF中, D'F=AD'·sin∠DAD'=90×sin60°=45 (厘米).
又∵CE=40(厘米), DE=30(厘米),∴FH=DC=DE+CE=70(厘米).
∴D'H=D'F+FH=(45+70)厘米.
答:点D'到BC的距离为(45+70)厘米;
(2)如图所示,连接AE,AE', EE'.
由题意得,AE'=AE,∠EAE'=60?,∴△AEE'是等边三角形.
∴EE'=AE.∵四边形ABCD是矩形,∴∠ADE=90°。
在Rt△ADE中,AD=90(厘米),DE=30(厘米)。
∴AE==(厘米),∴EE=30(厘米)。
答:E,E'两点的距离为30厘米。
_21?????????è?????(www.21cnjy.com)_
