第二十二章 四边形习题汇编
图片预览

文档简介
第二十二章 四边形 复习题
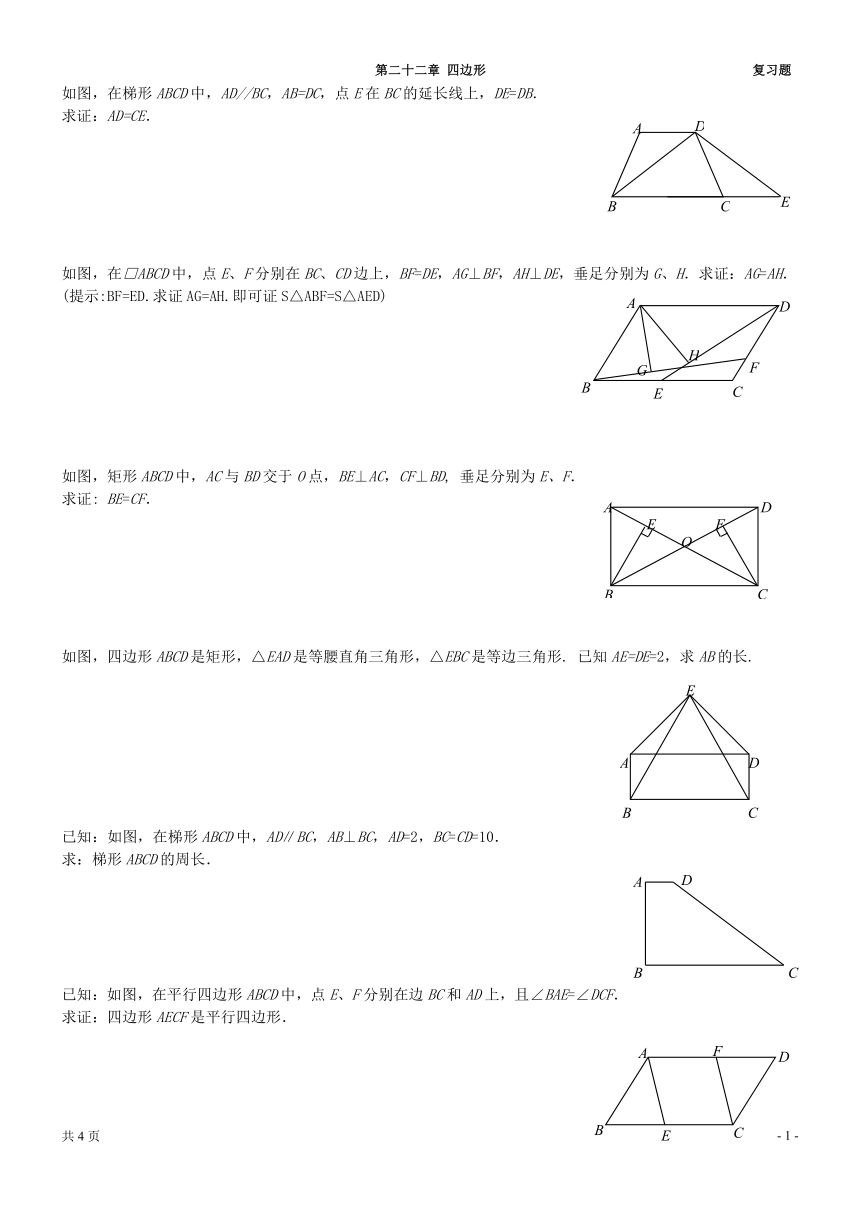
如图,在梯形ABCD中,AD//BC,AB=DC,点E在BC的延长线上,DE=DB.
求证:AD=CE.
如图,在□ABCD中,点E、F分别在BC、CD边上,BF=DE,AG⊥BF,AH⊥DE,垂足分别为G、H.求证:AG=AH.
(提示:BF=ED.求证AG=AH.即可证S△ABF=S△AED)
如图,矩形ABCD中,AC与BD交于O点,BE⊥AC,CF⊥BD, 垂足分别为E、F.
求证: BE=CF.
如图,四边形ABCD是矩形,△EAD是等腰直角三角形,△EBC是等边三角形. 已知AE=DE=2,求AB的长.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
求:梯形ABCD的周长.
已知:如图,在平行四边形ABCD中,点E、F分别在边BC和AD上,且∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
如图,在梯形中,,过对角线的中点作,分别交边于点,连接.求证:四边形是菱形;
如图,在Rt△ABC中,∠C=90°,D、E分别是边AC、AB的中点,过点B作BF⊥DE,交线段DE的延长线于为点F,过点C作CG⊥AB,交BF于点G,如果AC=2BC,
求证:(1)四边形BCDF是正方形;(2)AB=2CG.
如图,在□ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F,求证:四边形AFCE是菱形. (推理过程可以不写理由)
如图,在正方形ABCD中,H在BC上,EF⊥AH交AB于点E,交DC于点F.若AB=3,BH=1,求EF的长.
如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)
(1)连结 .
(2)猜想: = .
(3)证明(要求每步写出理由):
已知:如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,如果AE = CG,AH = CF,且EG平分。
(1) 求证:四边形EFGH是平行四边形;
(2) 求证:四边形EFGH是菱形。
如图,四边形ABCD是菱形,分别延长AB、BC、CD、DA到E、F、G、H点,使
AE=BF=CG=DH.求证:四边形EFGH是平行四边形.
如图,在四边形ABCD中,E、F、G、H分别是AD、BD、BC、AC上的中点,AB=5,CD=7.求四边形EFGH的周长.
如图,BD是△ABC的角平分线,EF是BD的中垂线,分别交AB于点E,AC于点F.
求证:四边形BFDE是菱形.
如图,四边形ABCD是正方形,延长边AD到E,使得CE∥BD.
(1)试比较正方形ABCD与△ABE面积的大小,并说明理由.
(2)如果条件“四边形ABCD是正方形”改为“四边形ABCD是梯形,AB∥CD”,其余条件都不变,那么梯形ABCD与△ABE面积的大小有什么关系?(只需写出结论,不必证明)
如图,在四边形ABCD中,对角线BD⊥AB,AD=20,AB=16,BC=15,CD=9,求证:四边形ABCD是梯形.
在等腰梯形ABCD中,AD∥BC,AB=CD=AD,AC⊥AB.求∠B的度数.
如图,已知:在梯形ABCD中,AD∥BC,AD+BC=CD ,M是AB的中点。
求证:DM、CM分别平分∠ADC和∠BCD
如图,在等腰梯形中,∥,,AB=12 cm,CD=6cm,点从开始沿边向以每秒3cm的速度移动,点从开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时运动停止。设运动时间为t秒。
(1)求证:当t=时,四边形是平行四边形;
(2)PQ是否可能平分对角线BD?若能,求出当t为何值时PQ平分BD;若不能,请说明理由;
(3)若△DPQ是以PQ为腰的等腰三角形,求t的值。
最后一题
(1)证明:∵当t=时,AP=3t=,DQ=6-t=,∴AP=DQ…………………(1分)
又∵∥,∴AP//DQ,∴是平行四边形………………(1分)
(2)能,当t=3时PQ平分BD………………(2分)
假设PQ平分对角线BD,设交点为M,即DM=MB,
∵AB//CD,∴∠1=∠2,
又∵∠3=∠4,∴△DQM≌△BPM,
∴DQ=PB,即6-t=12-3t,……………………(1分)
∴t=3……………………………………………(1分)
又可证明当t=3时DM=MB,∴当t=3时PQ平分BD。
(3)过D作DH⊥AB于H,
∵梯形中,AB=12 cm,CD=6cm
∴AH=3,DH= 4…………………………………(1分)
情况1:DP=PQ
过P作PM⊥CD于M,则DM=DQ=
∵PM⊥CD,DH⊥AB,∴PM//DH,又∥,∴DHPM为矩形,
∴HP=DM,即3t-3=∴t=……………………………………………………(1分)
∵0≤t≤4,≤4,∴t=符合题意
情况2:DQ=PQ(如图)
在Rt△QNP中,QP=6-t,PN=12-3t-3-t=9-4t,QN=4
∴…………………(1分)
整理得:
∵=
∴方程无解………………………………………………………………………(1分)
综上,若△DPQ是以PQ为边的等腰三角形,则t=
A
B
C
D
E
A
B
C
D
E
F
G
H
B
C
O
E
A
F
D
E
A
D
C
B
A
B
C
D
A
B
C
D
F
E
A
B
C
F
D
O
E
A
C
B
F
D
E
G
A
B
C
D
E
F
G
H
G
F
E
H
A
D
C
B
A
B
C
G
D
E
F
H
A
B
C
F
E
D
A
B
C
D
E
O
A
B
C
D
A
B
C
D
A
B
C
D
M
A
B
C
D
Q
P
2
A
B
C
D
·
·
Q
P
M
1
3
4
A
B
C
D
·
·
Q
P
M
H
A
B
C
D
·
·
Q
P
N
PAGE
- 5 -
共4页
如图,在梯形ABCD中,AD//BC,AB=DC,点E在BC的延长线上,DE=DB.
求证:AD=CE.
如图,在□ABCD中,点E、F分别在BC、CD边上,BF=DE,AG⊥BF,AH⊥DE,垂足分别为G、H.求证:AG=AH.
(提示:BF=ED.求证AG=AH.即可证S△ABF=S△AED)
如图,矩形ABCD中,AC与BD交于O点,BE⊥AC,CF⊥BD, 垂足分别为E、F.
求证: BE=CF.
如图,四边形ABCD是矩形,△EAD是等腰直角三角形,△EBC是等边三角形. 已知AE=DE=2,求AB的长.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
求:梯形ABCD的周长.
已知:如图,在平行四边形ABCD中,点E、F分别在边BC和AD上,且∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
如图,在梯形中,,过对角线的中点作,分别交边于点,连接.求证:四边形是菱形;
如图,在Rt△ABC中,∠C=90°,D、E分别是边AC、AB的中点,过点B作BF⊥DE,交线段DE的延长线于为点F,过点C作CG⊥AB,交BF于点G,如果AC=2BC,
求证:(1)四边形BCDF是正方形;(2)AB=2CG.
如图,在□ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F,求证:四边形AFCE是菱形. (推理过程可以不写理由)
如图,在正方形ABCD中,H在BC上,EF⊥AH交AB于点E,交DC于点F.若AB=3,BH=1,求EF的长.
如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)
(1)连结 .
(2)猜想: = .
(3)证明(要求每步写出理由):
已知:如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,如果AE = CG,AH = CF,且EG平分。
(1) 求证:四边形EFGH是平行四边形;
(2) 求证:四边形EFGH是菱形。
如图,四边形ABCD是菱形,分别延长AB、BC、CD、DA到E、F、G、H点,使
AE=BF=CG=DH.求证:四边形EFGH是平行四边形.
如图,在四边形ABCD中,E、F、G、H分别是AD、BD、BC、AC上的中点,AB=5,CD=7.求四边形EFGH的周长.
如图,BD是△ABC的角平分线,EF是BD的中垂线,分别交AB于点E,AC于点F.
求证:四边形BFDE是菱形.
如图,四边形ABCD是正方形,延长边AD到E,使得CE∥BD.
(1)试比较正方形ABCD与△ABE面积的大小,并说明理由.
(2)如果条件“四边形ABCD是正方形”改为“四边形ABCD是梯形,AB∥CD”,其余条件都不变,那么梯形ABCD与△ABE面积的大小有什么关系?(只需写出结论,不必证明)
如图,在四边形ABCD中,对角线BD⊥AB,AD=20,AB=16,BC=15,CD=9,求证:四边形ABCD是梯形.
在等腰梯形ABCD中,AD∥BC,AB=CD=AD,AC⊥AB.求∠B的度数.
如图,已知:在梯形ABCD中,AD∥BC,AD+BC=CD ,M是AB的中点。
求证:DM、CM分别平分∠ADC和∠BCD
如图,在等腰梯形中,∥,,AB=12 cm,CD=6cm,点从开始沿边向以每秒3cm的速度移动,点从开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时运动停止。设运动时间为t秒。
(1)求证:当t=时,四边形是平行四边形;
(2)PQ是否可能平分对角线BD?若能,求出当t为何值时PQ平分BD;若不能,请说明理由;
(3)若△DPQ是以PQ为腰的等腰三角形,求t的值。
最后一题
(1)证明:∵当t=时,AP=3t=,DQ=6-t=,∴AP=DQ…………………(1分)
又∵∥,∴AP//DQ,∴是平行四边形………………(1分)
(2)能,当t=3时PQ平分BD………………(2分)
假设PQ平分对角线BD,设交点为M,即DM=MB,
∵AB//CD,∴∠1=∠2,
又∵∠3=∠4,∴△DQM≌△BPM,
∴DQ=PB,即6-t=12-3t,……………………(1分)
∴t=3……………………………………………(1分)
又可证明当t=3时DM=MB,∴当t=3时PQ平分BD。
(3)过D作DH⊥AB于H,
∵梯形中,AB=12 cm,CD=6cm
∴AH=3,DH= 4…………………………………(1分)
情况1:DP=PQ
过P作PM⊥CD于M,则DM=DQ=
∵PM⊥CD,DH⊥AB,∴PM//DH,又∥,∴DHPM为矩形,
∴HP=DM,即3t-3=∴t=……………………………………………………(1分)
∵0≤t≤4,≤4,∴t=符合题意
情况2:DQ=PQ(如图)
在Rt△QNP中,QP=6-t,PN=12-3t-3-t=9-4t,QN=4
∴…………………(1分)
整理得:
∵=
∴方程无解………………………………………………………………………(1分)
综上,若△DPQ是以PQ为边的等腰三角形,则t=
A
B
C
D
E
A
B
C
D
E
F
G
H
B
C
O
E
A
F
D
E
A
D
C
B
A
B
C
D
A
B
C
D
F
E
A
B
C
F
D
O
E
A
C
B
F
D
E
G
A
B
C
D
E
F
G
H
G
F
E
H
A
D
C
B
A
B
C
G
D
E
F
H
A
B
C
F
E
D
A
B
C
D
E
O
A
B
C
D
A
B
C
D
A
B
C
D
M
A
B
C
D
Q
P
2
A
B
C
D
·
·
Q
P
M
1
3
4
A
B
C
D
·
·
Q
P
M
H
A
B
C
D
·
·
Q
P
N
PAGE
- 5 -
共4页
