第二章 图形与变换当堂检测(文)

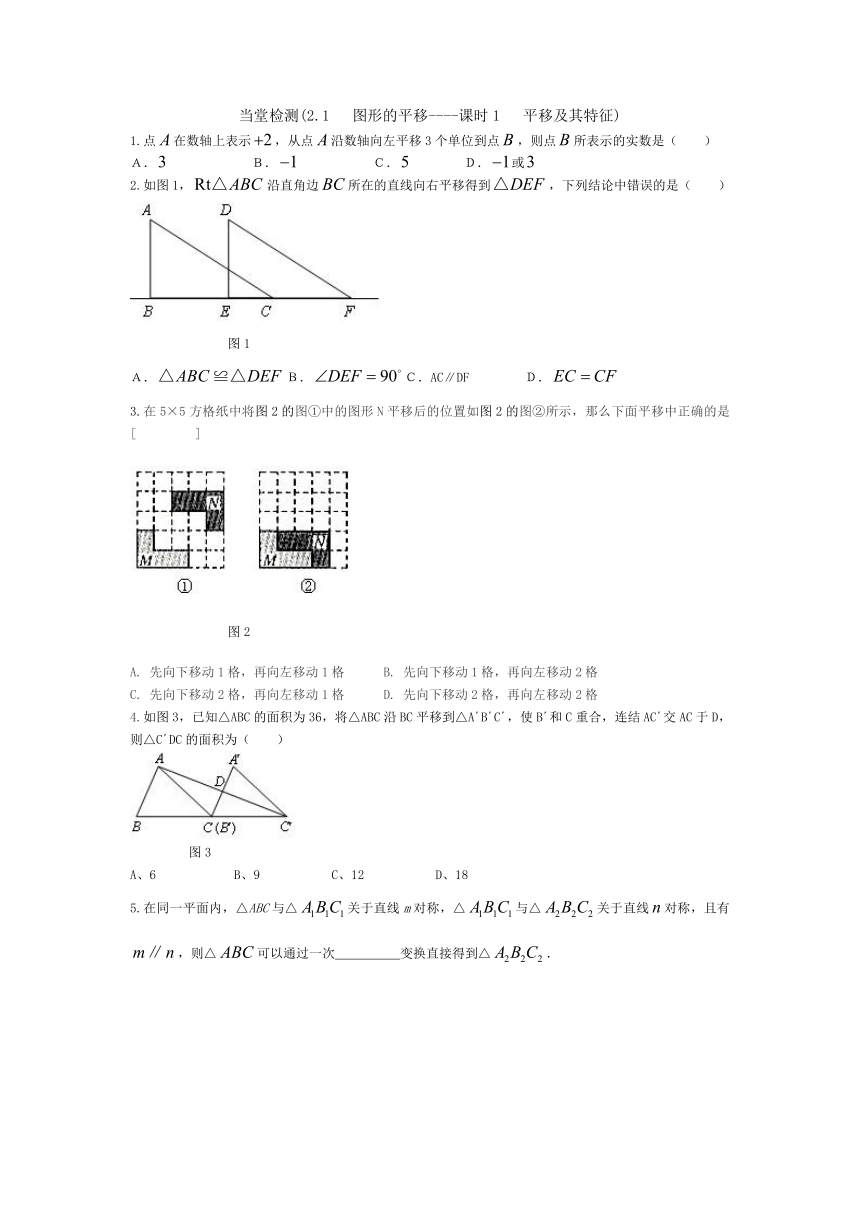
当堂检测(2.1 图形的平移----课时1 平移及其特征)
1.点在数轴上表示，从点沿数轴向左平移3个单位到点，则点所表示的实数是（　　）
Ａ． Ｂ． Ｃ． Ｄ．或
2.如图1，沿直角边所在的直线向右平移得到，下列结论中错误的是（　　）
图1
Ａ．Ｂ．Ｃ．AC∥DF Ｄ．
3.在5×5方格纸中将图2的图①中的图形N平移后的位置如图2的图②所示，那么下面平移中正确的是[ ]
图2
A. 先向下移动1格，再向左移动1格 B. 先向下移动1格，再向左移动2格
C. 先向下移动2格，再向左移动1格 D. 先向下移动2格，再向左移动2格
4.如图3，已知△ABC的面积为36，将△ABC沿BC平移到△A B C ，使B 和C重合，连结AC 交AC于D，则△C DC的面积为（　　）
图3
A、6　　 B、9　　 C、12　　 D、18
5.在同一平面内，△ABC与△关于直线m对称，△与△关于直线对称，且有，则△可以通过一次　　　　 变换直接得到△．
当堂检测(2.1图形的平移----课时2 平移与坐标)
1.将点向左平移1个单位，再向下平移2个单位后得到对应点的坐标是 ．
2.(2009年湖南常德)如图4，△ABC向右平移4个单位后得到△A′B′C′，则A′点的坐标是 　 ．
图4
3.(2009湖南张家界)将函数的图象向上平移2个单位，得到函数 的图象．
4.(2009广西梧州)将点A（1，－3）向右平移2个单位，再向下平移2个单位后得到点B（a，b），则ab＝__________．
5.如图5，矩形PMON的边OM，ON分别在坐标轴上，且点P的坐标为（-2，3）。将矩形PMON沿x轴正方向平移4个单位，得到矩形
图5
（1）请在上图的直角坐标系中画出平移后的像；
（2）求直线OP的函数解析式.
当堂检测(2.2图形的旋转--课时1 旋转及其性质)
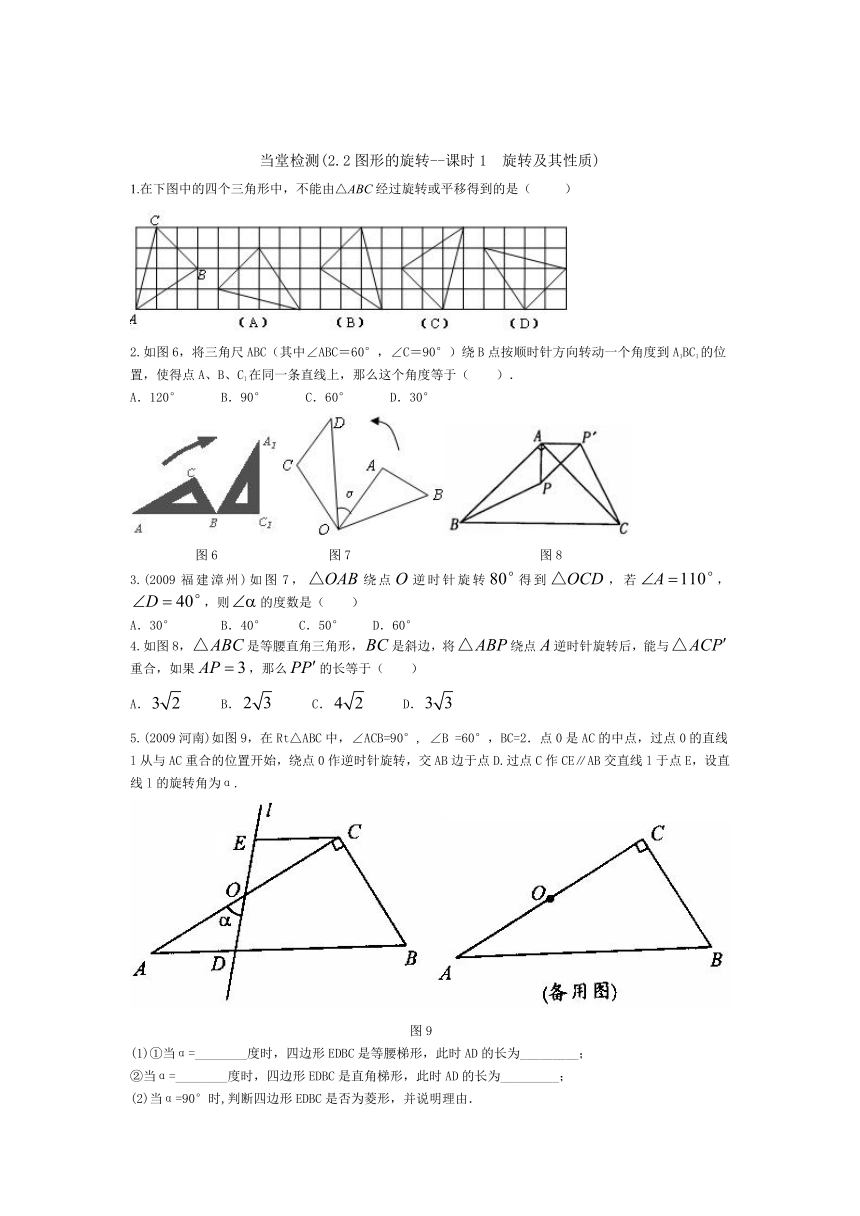
1.在下图中的四个三角形中，不能由△ABC经过旋转或平移得到的是（ ）
2.如图6，将三角尺ABC（其中∠ABC＝60°，∠C＝90°）绕B点按顺时针方向转动一个角度到A1BC1的位置，使得点A、B、C1在同一条直线上，那么这个角度等于（ ）．
A．120° B．90° C．60° D．30°
图6 图7 图8
3.(2009福建漳州)如图7，绕点逆时针旋转得到，若，，则的度数是（ ）
A．30° B．40° C．50° D．60°
4.如图8，是等腰直角三角形，是斜边，将绕点逆时针旋转后，能与重合，如果，那么的长等于（ ）
A． B． C． D．
5.(2009河南)如图9，在Rt△ABC中，∠ACB=90°, ∠B =60°，BC=2．点0是AC的中点，过点0的直线l从与AC重合的位置开始，绕点0作逆时针旋转，交AB边于点D.过点C作CE∥AB交直线l于点E，设直线l的旋转角为α.
图9
(1)①当α=________度时，四边形EDBC是等腰梯形，此时AD的长为_________；
②当α=________度时，四边形EDBC是直角梯形，此时AD的长为_________；
(2)当α=90°时,判断四边形EDBC是否为菱形，并说明理由．
当堂检测(2.2图形的旋转--课时2 旋转作图与坐标)
1.正方形ABCD在坐标系中的位置如图10所示，将正方形ABCD绕D点顺时针旋转90°后，B点的坐标为（ ）
A、（－2，2） B、（4，1） C、（3，1） D、（4，0）
图10 图11
2.如图11，△ABC的顶点坐标分别为A ( 3，6 )、B ( 1，3 )、C ( 4，2 ) ．如果将△ABC绕C点顺时针旋转90 ，得到△A′B′C′，那么点A的对应点A′ 的坐标为（ ）.
3.如图12，O是外一点。以点O为旋转中心，将按逆时针方向旋转80°，作出旋转变换后的图形。
图12 图13
4.如图13，已知:
（1） AC的长等于_______．
（2）若将向右平移2个单位得到，则点的对应点的坐标是______；
（3） 若将绕点按顺时针方向旋转后得到A1B1C1，则A点对应点A1的坐标是_________．
5.如图14，在网格中有一个四边形图案．
图14
(1)请你画出此图案绕点D顺时针方向旋转900，1800，2700的图案，你会得到一个美丽的图案，千万不要将阴影位置涂错；
(2)若网格中每个小正方形的边长为l，旋转后点A的对应点依次为A1、A2、A3，求四边形AA1A2A3的面积；
(3)这个美丽图案能够说明一个著名结论的正确性，请写出这个结论．
当堂检测(2.3 图形的位似)
1.如图15，已知△EFH和△MNK是位似图形，那么其位似中心是点 ( )
图15
2.如图16，五边形ABCDE与五边形A′B′C′D′E′是位似图形，O为位似中心，OD=OD′，则A′B′:AB为（　　）
图16 图17
A.2:3 B.3:2 C.1:2 D.2:1
3.如图17，小“鱼”与大“鱼”是位似图形，已知小“鱼”上一个“顶点”的坐标为，那么大“鱼”上对应“顶点”的坐标为（　　）
Ａ． Ｂ． Ｃ． Ｄ．
4.如图18，方格纸中有一条美丽可爱的小金鱼．
图18
（1）在同一方格纸中，画出将小金鱼图案绕原点O旋转180°后得到的图案；（4分）
（2）在同一方格纸中，并在轴的右侧，将原小金鱼图案以原点O为位似中心放大，使它们的位似比为1：2，画出放大后小金鱼的图案．
当堂检测答案
2.1 图形的平移
课时1 平移及其特征
1.B 2.D 3.C 4.D 5.平移
课时2 平移与坐标
1.(0，0) 2.（1，2） 3. 4.-15
5.解析：（1）如图所示:
图2-36
（2）设直线OP的函数解析式为：y=kx,
因为点P的坐标为（－2，3），代入，得3＝－2k,
即直线OP的函数解析式为：
2.2图形的旋转
课时1 旋转及其性质
1.B 2.A 3.C 4.A
5.（1）①30，1；②60，1.5；
（2）当∠α=900时，四边形EDBC是菱形.
∵∠α=∠ACB=900，∴BC//ED.
∵CE//AB, ∴四边形EDBC是平行四边形.
在Rt△ABC中，∠ACB=900，∠B=600,BC=2,
∴∠A=300.
∴AB=4,AC=2.
∴AO== .
在Rt△AOD中，∠A=300，∴AD=2.
∴BD=2.
∴BD=BC.
又∵四边形EDBC是平行四边形，
∴四边形EDBC是菱形.
课时2 旋转作图与坐标
1.D 2.（8，3）
3.解：如图所示，（1）以点O为旋转中心，分别把点A,B,C按逆时针方向旋转80°，得点、、.
(2)连结，，。则就是所求作的旋转变换后的图形。
4.解：（1）． （2）（1，2）． （3）（3，0）．
5.解：(1)如图所示；
(2)如图，=-4 =(3+5)2-4××3×5 =34
故四边形似AA1A2A3的面积为34．
(3)结论：AB2+BC2=AC2或勾股定理的文字叙述
2.3 图形的位似
1.B 2.D 3.C
4. 解：