北京版六上 5.4 扇形 习题 (含答案)
文档属性
| 名称 | 北京版六上 5.4 扇形 习题 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 99.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览




文档简介
5.4 扇形
一、单选题
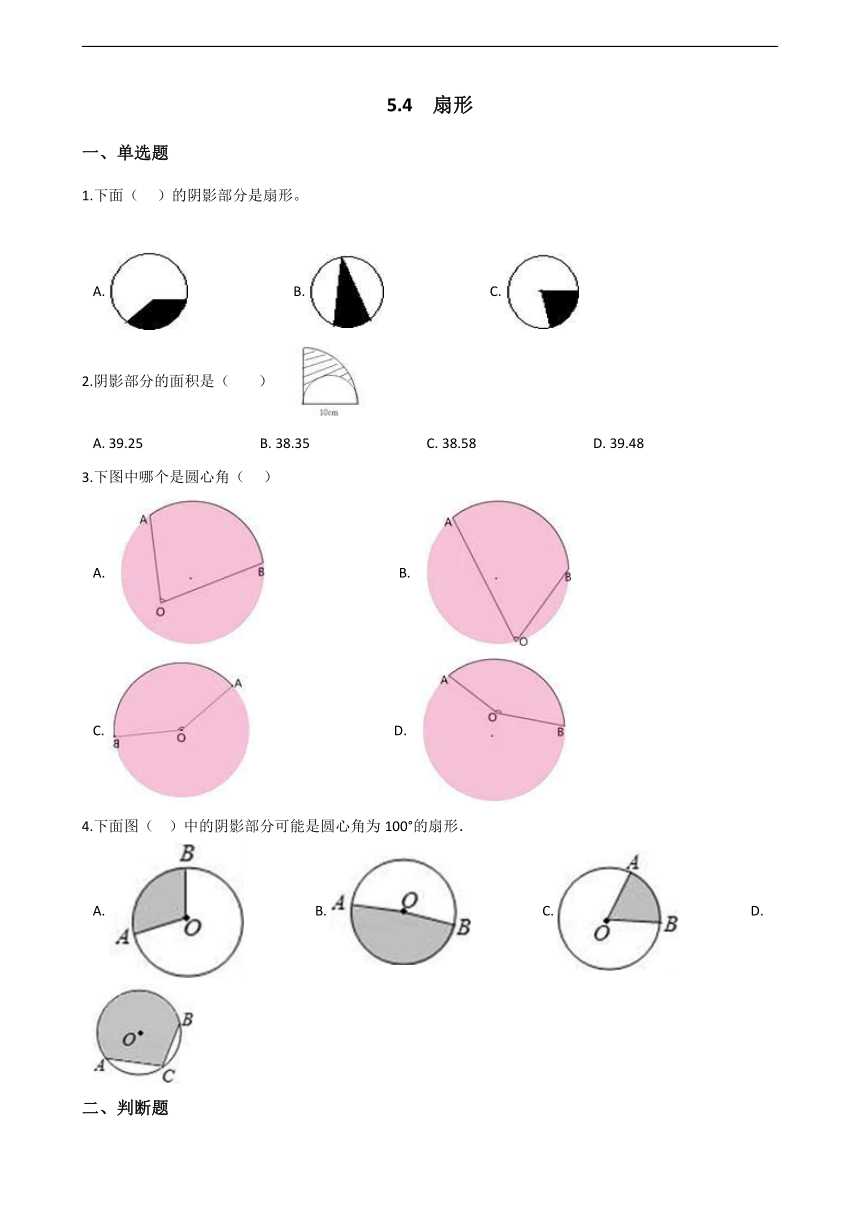
1.下面(??? )的阴影部分是扇形。
A.????????????????????????????????B.????????????????????????????????C.?
2.阴影部分的面积是(???? ??) ??
A.?39.25??????????????????????????????????B.?38.35??????????????????????????????????C.?38.58??????????????????????????????????D.?39.48
3.下图中哪个是圆心角(??? )
A.?? ???????????????????????????????????????B.??
C.??????????????????????????????????????????D.??
4.下面图(?? )中的阴影部分可能是圆心角为100°的扇形.
A.??????????????????????B.??????????????????????C.??????????????????????D.?
二、判断题
5.在一个圆内,剪去一个扇形后,剩下的部分仍是扇形。
6.顶点在圆上的角叫圆心角。
7.把一个圆分成5份,每一份都一定是个扇形。
8.圆心角越大,扇形的面积就越大.(判断对错)
三、填空题
9.扇形的周长包括一段________的长度和两条________的长度。
10.下面图形中哪些角是圆心角?在(?? )里画“√”。
11.圆心角是90°的扇形面积是它所在圆面积的________?
12.下图中有________个扇形.
四、解答题
13.下图是一个三角形,以它的每个顶点为圆心,以2cm为半径画弧,求阴影部分的面积。
14.东风小学六年级二班上学期期末的数学成绩情况为优秀14人,良好16人,及格8人,不及格2人。每种成绩的人数各占全班人数的百分之几?把这次的数学成绩用扇形统计图表示出来。
五、应用题
15.如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取3.14)
参考答案
一、单选题
1.【答案】C
【解析】【解答】根据分析可知,A、B图中都不是由半径和圆弧组成的,不是扇形,C图阴影部分是扇形.
故答案为:C.
【分析】根据扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此判断即可.
2.【答案】 A
【解析】【解答】解:3.14×10?×-3.14×(10÷2)?×
=3.14×25-3.14×12.5
=3.14×12.5
=39.25(cm?)
故答案为:A
【分析】图中阴影部分的面积是半径10cm的扇形面积减去直径10cm的圆面积的一半,由此根据扇形面积公式计算即可.
3.【答案】 C
【解析】【解答】解:根据扇形圆心角的定义可知,只有C图中的才是圆心角,A、B、D的角都不在圆心上,都不是圆心角.
故答案为:C
【分析】顶点在圆心的角才叫做圆心角,因此根据圆心角的定义判断即可.
4.【答案】 A
【解析】【解答】A、这个阴影部分可能是圆心角为100°的扇形;
B、这个圆心角接近一个平角,故不可能是圆心角为100°的扇形;
C、这个圆心角小于直角,故不可能是圆心角为100°的扇形;
D、这个角不是圆心角。
故答案为:A。
【分析】圆心角是指以顶点为圆心,以两条半径为边的角。这个圆心角与它所对的弧围成的图形就是扇形。根据这个定义结合各选项看哪个图形的圆心角可能是100°。
二、判断题
5.【答案】正确
【解析】【解答】在一个圆内,剪去一个扇形后,剩下的部分仍是扇形,原题说法正确.
故答案为:正确.
【分析】根据扇形的定义:圆上的弧与它所对圆心角的组成的图形叫扇形,同一个圆内,剪去一个扇形后,剩下的部分仍是扇形.
6.【答案】正确
【解析】【解答】解:顶点在圆上的角叫圆心角。原题说法正确。
故答案为:正确
【分析】一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形,这两条半径组成的角就是圆心角。
7.【答案】错误
【解析】【解答】解:把一个圆分成5份,每一份不一定是扇形。原题说法错误。
故答案为:错误。
【分析】只有以圆心角为中心,沿着圆的半径把圆分成5份,这样才能分成5个扇形。
8.【答案】错误
【解析】【解答】解:由分析知:扇形的面积大小与圆心角、半径有关系,圆心角越大,半径不一定它的,所以面积无法确定;
因此题干的说法是错误的.
故答案为:错误.
【分析】根据“扇形的面积= 知:扇形的面积大小与圆心角、半径有关系,圆心角越大,半径不一定越大,所以面积无法确定;进而判断即可.
三、填空题
9.【答案】弧;半径
【解析】【解答】扇形的周长包括一段弧的长度和两条半径的长度.
故答案为:弧;半径.
【分析】围成一个封闭图形一周的长度之和是图形的周长,根据对扇形的认识可知,扇形的周长包括一段弧的长度和两条半径的长度.
10.【答案】
【解析】【分析】圆心角的顶点都在圆心上,两条边是圆的半径。由此判断即可。
11.【答案】
【解析】【解答】解:90°÷360°=
故答案为:
【分析】扇形圆心角度数是360°的几分之几,扇形面积就是所在圆面积的几分之几,用除法计算圆心角的度数是360°的几分之几即可.
12.【答案】3
【解析】【解答】解:根据对扇形的认识可知:图中有3个扇形.故答案为:3.
【分析】扇形是圆的一部分,图中的扇形的半径分别是AF、AE、AD,三个扇形的圆心角是相同的.
四、解答题
13.【答案】 3.14×2?÷2
=3.14×4÷2
=3.14×2
=6.28(cm?)
答:阴影部分的面积是6.28cm?。
【解析】【分析】采用割补的办法将三个圆弧拼合在一起,组成一个圆心角为180°的圆弧,即为半圆,求出半圆的面积即可(阴影部分面积=πr?÷2)。
14.【答案】 全班人数:14+16+8+2=40(人)
优秀:14÷40=35% 360°×35%=126°
良好:16÷40=40% ?? 360°×40%=144°
及格:8÷40=20% ??? 360°×20%=72°
不及格:2÷40=5% ?? 360°×5%=18°
【解析】【解答】 全班人数:14+16+8+2=40(人);
优秀:14÷40=35%,360°×35%=126°;
良好:16÷40=40%,360°×40%=144°;
及格:8÷40=20%,360°×20%=72°;
不及格:2÷40=5%,360°×5%=18°;
根据计算,作图如下:
【分析】根据题意可知,先求出全班的总人数,将各种成绩的人数相加,再用每种成绩的人数÷全班总人数=每种成绩的人数占全班人数的百分比,根据圆周角是360°,分别求出各部分占的圆心角的度数,据此画出扇形统计图.
五、应用题
15.【答案】解:AC的长为2厘米,半径为1厘米,
正方形外阴影部分的面积为:3.14×12× ﹣2×1÷2
=3.14× ﹣1,
=1.57﹣1,
=0.57(平方厘米);
正方形内阴影部分的面积为:3.14×2× ﹣2÷2
=6.28× ﹣1,
=1.57﹣1,
=0.57(平方厘米),
0.57+0.57=1.14(平方厘米);
答:阴影部分的面积为1.14平方厘米
【解析】【分析】根据图示可知,影部分的面积等于正方形外阴影部分的面积加上正方形内阴影部分的面积,扇形ABC是以AC为直径的圆的面积的一半,可用以AC为直径的圆的面积的一半减去正方形面积的一半就是正方形外阴影部分的面积,正方形内阴影部分的面积等于以AD为半径的 圆的面积减去三角形ACD的面积,列式解答即可得到答案.解答此题的关键是将阴影部分的面积分为正方形内与正方形外两部分,然后再根据圆的面积公式,正方形的面积公式进行计算即可.
一、单选题
1.下面(??? )的阴影部分是扇形。
A.????????????????????????????????B.????????????????????????????????C.?
2.阴影部分的面积是(???? ??) ??
A.?39.25??????????????????????????????????B.?38.35??????????????????????????????????C.?38.58??????????????????????????????????D.?39.48
3.下图中哪个是圆心角(??? )
A.?? ???????????????????????????????????????B.??
C.??????????????????????????????????????????D.??
4.下面图(?? )中的阴影部分可能是圆心角为100°的扇形.
A.??????????????????????B.??????????????????????C.??????????????????????D.?
二、判断题
5.在一个圆内,剪去一个扇形后,剩下的部分仍是扇形。
6.顶点在圆上的角叫圆心角。
7.把一个圆分成5份,每一份都一定是个扇形。
8.圆心角越大,扇形的面积就越大.(判断对错)
三、填空题
9.扇形的周长包括一段________的长度和两条________的长度。
10.下面图形中哪些角是圆心角?在(?? )里画“√”。
11.圆心角是90°的扇形面积是它所在圆面积的________?
12.下图中有________个扇形.
四、解答题
13.下图是一个三角形,以它的每个顶点为圆心,以2cm为半径画弧,求阴影部分的面积。
14.东风小学六年级二班上学期期末的数学成绩情况为优秀14人,良好16人,及格8人,不及格2人。每种成绩的人数各占全班人数的百分之几?把这次的数学成绩用扇形统计图表示出来。
五、应用题
15.如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取3.14)
参考答案
一、单选题
1.【答案】C
【解析】【解答】根据分析可知,A、B图中都不是由半径和圆弧组成的,不是扇形,C图阴影部分是扇形.
故答案为:C.
【分析】根据扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此判断即可.
2.【答案】 A
【解析】【解答】解:3.14×10?×-3.14×(10÷2)?×
=3.14×25-3.14×12.5
=3.14×12.5
=39.25(cm?)
故答案为:A
【分析】图中阴影部分的面积是半径10cm的扇形面积减去直径10cm的圆面积的一半,由此根据扇形面积公式计算即可.
3.【答案】 C
【解析】【解答】解:根据扇形圆心角的定义可知,只有C图中的才是圆心角,A、B、D的角都不在圆心上,都不是圆心角.
故答案为:C
【分析】顶点在圆心的角才叫做圆心角,因此根据圆心角的定义判断即可.
4.【答案】 A
【解析】【解答】A、这个阴影部分可能是圆心角为100°的扇形;
B、这个圆心角接近一个平角,故不可能是圆心角为100°的扇形;
C、这个圆心角小于直角,故不可能是圆心角为100°的扇形;
D、这个角不是圆心角。
故答案为:A。
【分析】圆心角是指以顶点为圆心,以两条半径为边的角。这个圆心角与它所对的弧围成的图形就是扇形。根据这个定义结合各选项看哪个图形的圆心角可能是100°。
二、判断题
5.【答案】正确
【解析】【解答】在一个圆内,剪去一个扇形后,剩下的部分仍是扇形,原题说法正确.
故答案为:正确.
【分析】根据扇形的定义:圆上的弧与它所对圆心角的组成的图形叫扇形,同一个圆内,剪去一个扇形后,剩下的部分仍是扇形.
6.【答案】正确
【解析】【解答】解:顶点在圆上的角叫圆心角。原题说法正确。
故答案为:正确
【分析】一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形,这两条半径组成的角就是圆心角。
7.【答案】错误
【解析】【解答】解:把一个圆分成5份,每一份不一定是扇形。原题说法错误。
故答案为:错误。
【分析】只有以圆心角为中心,沿着圆的半径把圆分成5份,这样才能分成5个扇形。
8.【答案】错误
【解析】【解答】解:由分析知:扇形的面积大小与圆心角、半径有关系,圆心角越大,半径不一定它的,所以面积无法确定;
因此题干的说法是错误的.
故答案为:错误.
【分析】根据“扇形的面积= 知:扇形的面积大小与圆心角、半径有关系,圆心角越大,半径不一定越大,所以面积无法确定;进而判断即可.
三、填空题
9.【答案】弧;半径
【解析】【解答】扇形的周长包括一段弧的长度和两条半径的长度.
故答案为:弧;半径.
【分析】围成一个封闭图形一周的长度之和是图形的周长,根据对扇形的认识可知,扇形的周长包括一段弧的长度和两条半径的长度.
10.【答案】
【解析】【分析】圆心角的顶点都在圆心上,两条边是圆的半径。由此判断即可。
11.【答案】
【解析】【解答】解:90°÷360°=
故答案为:
【分析】扇形圆心角度数是360°的几分之几,扇形面积就是所在圆面积的几分之几,用除法计算圆心角的度数是360°的几分之几即可.
12.【答案】3
【解析】【解答】解:根据对扇形的认识可知:图中有3个扇形.故答案为:3.
【分析】扇形是圆的一部分,图中的扇形的半径分别是AF、AE、AD,三个扇形的圆心角是相同的.
四、解答题
13.【答案】 3.14×2?÷2
=3.14×4÷2
=3.14×2
=6.28(cm?)
答:阴影部分的面积是6.28cm?。
【解析】【分析】采用割补的办法将三个圆弧拼合在一起,组成一个圆心角为180°的圆弧,即为半圆,求出半圆的面积即可(阴影部分面积=πr?÷2)。
14.【答案】 全班人数:14+16+8+2=40(人)
优秀:14÷40=35% 360°×35%=126°
良好:16÷40=40% ?? 360°×40%=144°
及格:8÷40=20% ??? 360°×20%=72°
不及格:2÷40=5% ?? 360°×5%=18°
【解析】【解答】 全班人数:14+16+8+2=40(人);
优秀:14÷40=35%,360°×35%=126°;
良好:16÷40=40%,360°×40%=144°;
及格:8÷40=20%,360°×20%=72°;
不及格:2÷40=5%,360°×5%=18°;
根据计算,作图如下:
【分析】根据题意可知,先求出全班的总人数,将各种成绩的人数相加,再用每种成绩的人数÷全班总人数=每种成绩的人数占全班人数的百分比,根据圆周角是360°,分别求出各部分占的圆心角的度数,据此画出扇形统计图.
五、应用题
15.【答案】解:AC的长为2厘米,半径为1厘米,
正方形外阴影部分的面积为:3.14×12× ﹣2×1÷2
=3.14× ﹣1,
=1.57﹣1,
=0.57(平方厘米);
正方形内阴影部分的面积为:3.14×2× ﹣2÷2
=6.28× ﹣1,
=1.57﹣1,
=0.57(平方厘米),
0.57+0.57=1.14(平方厘米);
答:阴影部分的面积为1.14平方厘米
【解析】【分析】根据图示可知,影部分的面积等于正方形外阴影部分的面积加上正方形内阴影部分的面积,扇形ABC是以AC为直径的圆的面积的一半,可用以AC为直径的圆的面积的一半减去正方形面积的一半就是正方形外阴影部分的面积,正方形内阴影部分的面积等于以AD为半径的 圆的面积减去三角形ACD的面积,列式解答即可得到答案.解答此题的关键是将阴影部分的面积分为正方形内与正方形外两部分,然后再根据圆的面积公式,正方形的面积公式进行计算即可.
