北京版六上 5.3 圆的面积 习题(含答案)
文档属性
| 名称 | 北京版六上 5.3 圆的面积 习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 137.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
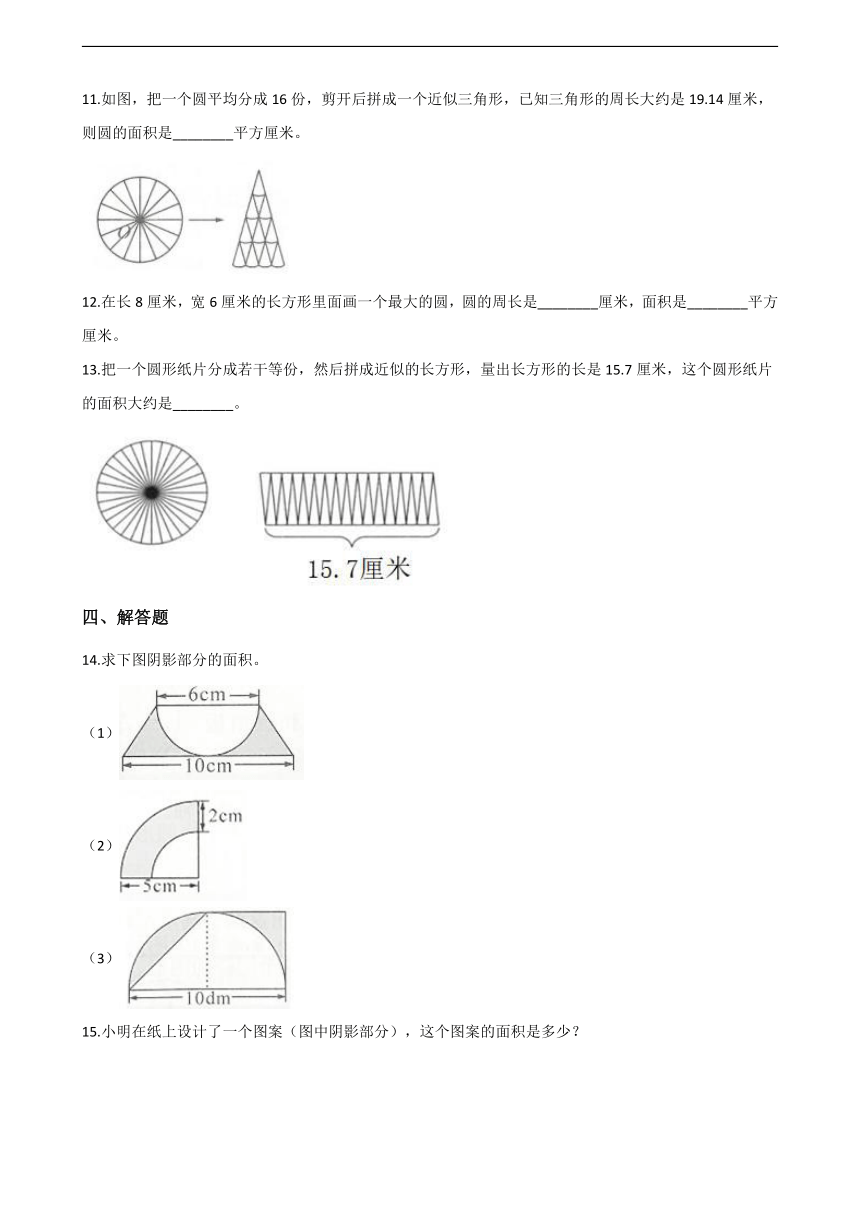
图片预览



文档简介
5.3 圆的面积
一、单选题
1.世界上第一个把圆周率的值精确到六位小数的数学家是( ??)
A.?刘徽??????????????????????????????????????B.?祖冲之??????????????????????????????????????C.?欧几里德
2.半径是3cm的圆,下列关于这个圆的数据正确的是(??? )
A.?直径9cm????????????????????B.?周长18.84cm????????????????????C.?周长9.42cm????????????????????D.?面积113.04cm2
3.在正方形铁皮上剪下一个圆和一个扇形,恰好围成一个圆锥模型(如右图)。如果圆的半径为r,扇形半径为R,那么R是r的(??? )
A.?6倍???????????????????????????????????????????B.?3倍???????????????????????????????????????????C.?4倍
4.下面三个正方形的边长相等,各图中的阴影部分的面积相比较,(??? )。
A.?图一最大?????????????????????????????B.?图二最大?????????????????????????????C.?图三最大?????????????????????????????D.?一样大
二、判断题
5.直径是3厘米的圆比直径是2厘米的圆的圆周率大.
6.一个圆的周长是它直径的π倍。
7.当圆的半径是2 cm时,它的周长和面积相等。
8.圆周长是直径的3.14倍.
三、填空题
9.圆的公式C=________=________,S=________
10.画一个直径是5厘米的圆,圆规两脚之间的距离是________厘米。如果要画一个周长是12.56厘米的圆,圆规两脚之间的距离应该是________厘米,这个圆的面积是________平方厘米。
11.如图,把一个圆平均分成16份,剪开后拼成一个近似三角形,已知三角形的周长大约是19.14厘米,则圆的面积是________平方厘米。
12.在长8厘米,宽6厘米的长方形里面画一个最大的圆,圆的周长是________厘米,面积是________平方厘米。
13.把一个圆形纸片分成若干等份,然后拼成近似的长方形,量出长方形的长是15.7厘米,这个圆形纸片的面积大约是________。
四、解答题
14.求下图阴影部分的面积。
(1)
(2)
(3)
15.小明在纸上设计了一个图案(图中阴影部分),这个图案的面积是多少?
五、应用题
16.从一张正方形纸上剪下一个周长是18.84厘米的最大圆,求被剪掉的纸屑的面积。
参考答案
一、单选题
1.【答案】 B
【解析】【解答】世界上第一个把圆周率的值精确到六位小数的数学家是祖冲之。
故答案为:B。
【分析】阿基米德是世界上最早进行圆周率计算的,汉朝数学家刘徽将圆周率的值进一步精确了,南北朝数学家祖冲之把π的值精确至小数点后六位,即3.1415926与3.1415927之间,这是当时世界上算得最精确的数值。
2.【答案】 B
【解析】【解答】解:A:直径:3×2=6(cm)。此选项错误;
B:周长:3.14×3×2=18.84(cm)。此选项正确;
C:周长的计算错误;
D:面积:3.14×32=28.26(cm2).此选项错误。
故答案为:B。
【分析】同一个圆内,圆的直径是半径的2倍,圆周长公式:C=2r,圆面积公式:S=, 根据公式计算后选择即可。
3.【答案】 C
【解析】【解答】观察图可得:
2×π×R×=2×π×r
????????? πR=2πr
??? πR÷2π=2πr÷2π
?????????????? =r
?????????? ×4=r×4
???????????????? R=4r
R÷r=4
故答案为:C。
【分析】根据题意可知,小圆的周长等于半径为R的大圆的周长的, 据此列方程,求出R与r的关系。
4.【答案】 D
【解析】【解答】解:三个图中阴影部分的面积都是正方形面积减去一个圆的面积,阴影部分的面积是相等的。
故答案为:D。
【分析】阴影部分的面积都是正方形面积减去空白部分圆的面积,图二空白部分是两个半圆,组合后就是一个整圆;图三空白部分是四个扇形,组合后也是一个圆的面积。
二、判断题
5.【答案】 错误
【解析】【解答】所有圆的圆周率都是一样的,原题说法错误。
故答案为:错误。
【分析】 圆周率指圆的周长与直径的比值,用π表示,圆周率是不变的,据此判断。
6.【答案】正确
【解析】【解答】一个圆的周长是它直径的π倍,此题说法正确.
故答案为:正确.
【分析】根据圆周率的定义可知,圆周率是圆的周长与直径的比值,一般用希腊字母π表示,一个圆的周长是它直径的π倍,据此判断.
7.【答案】 错误
【解析】【解答】解:周长和面积的意义是不同的,无法比较大小。原题说法错误。
故答案为:错误。
【分析】圆的周长是一周的长度,圆的面积是图形的大小,意义不同,单位也不同,面积和周长是无法比较大小的。
8.【答案】 错误
【解析】【解答】圆周长不是直径的3.14倍,说法错误。
故答案为:错误。
【分析】一个圆的周长总是直径的π倍,π约等于3.14,并不等于3.14,所以说:一个圆的周长总是直径的3.14倍是错误的,应该说:一个圆的周长总是直径的π倍。
三、填空题
9.【答案】2πr;πd;πr2
【解析】【解答】解:圆的公式:C=2πr=πd,S=πr?
故答案为:2πr;πd;πr?【分析】圆的周长是直径的π倍,是半径是2π倍,圆的面积是半径的平方乘圆周率,用字母表示这些公式即可。
10.【答案】2.5;2;12.56
【解析】【解答】5÷2=2.5(厘米)
12.56÷2÷3.14
=6.28÷3.14
=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
故答案为:2.5;2;12.56【分析】根据对圆的认识可知,圆规两脚之间的距离是半径,已知圆的直径,求半径,用直径÷2=半径;已知圆的周长,求圆的半径,用公式:C÷2÷π=r,据此列式计算;要求圆的面积,用公式:S=πr2 , 据此列式解答.
11.【答案】 12.56
【解析】【解答】设圆的半径是r,则 ? 8r+=19.14
? ? ?? ? 8r+=19.14
?? ????? 16r+πr=38.28
?????????? 19.14r=38.28
19.14r÷19.14=38.28÷19.14
??????????????????? r=2
圆的面积:
3.14×22
=3.14×4
=12.56(cm2)
故答案为:12.56 。
【分析】观察图可知,把一个圆平均分成16份,剪开后拼成一个近似三角形,设圆的半径是r,三角形的周长=圆的半径×8+圆的周长,据此列方程解答,求出圆的半径,然后用公式:S=πr2 , 据此解答。
12.【答案】 18.84;28.26
【解析】【解答】解:6×3.14=18.84厘米,所以圆的周长是18.84厘米;(6÷2)2×3.14=28.26平方厘米,所以面积是28.26平方厘米。
故答案为:18.84;28.26。
【分析】在一个长方形中画一个最大的圆,这个圆的直径就是长方形的宽,所以圆的周长=圆的直径×π,圆的面积=πr2 , 其中圆的半径=圆的直径÷2。
13.【答案】 25π平方厘米(或78.5平方厘米)
【解析】【解答】解:半径:15.7×2÷3.14÷2=5(厘米)
面积:3.14×52=3.14×25=78.5(平方厘米)
故答案为:78.5平方厘米。
【分析】15.7厘米是圆周长的一半,因此根据圆周长公式先计算出圆的半径,然后根据圆面积公式计算面积。
四、解答题
14.【答案】 (1)解:(10+6)×3÷2-3.14×(6÷2)2÷2=9.87(cm2)
(2)解: ×(52-32)×3.14=12.56(cm2)
(3)解:10÷2=5(dm)
5×5÷2=12.5(dm2)
【解析】【分析】(1)观察图可知,阴影部分的面积=梯形面积-空白半圆的面积,据此列式解答;
(2)观察图可知,阴影部分的面积=圆环的面积×, 据此列式解答;
(3)观察图可知,通过剪拼,可以将两个阴影部分拼成一个底与高都是5dm的直角三角形,根据三角形的面积=底×高÷2,据此列式解答。
15.【答案】 解:3.14×(10÷2)2﹣3.14×(4÷2)2
=3.14×25﹣3.14×4
=78.5﹣12.56
=65.94(平方厘米)
答:阴影部分的面积是65.94平方厘米。
【解析】【分析】从图中可以看出,阴影部分的面积=大圆的面积-小圆的面积,圆的面积=(圆的直径÷2)2×π,据此代入数据作答即可。
五、应用题
16.【答案】解:半径:18.84÷3.14÷2=3(厘米),边长:3×2=6(厘米),
剪掉的面积:
6×6-3.14×3?
=36-28.26
=7.74(平方厘米)
答:被剪掉的纸屑面积是7.74平方厘米。
【解析】【分析】这个圆的直径就是正方形的边长,用圆的周长除以3.14再除以2求出半径,然后计算出正方形的边长,用正方形面积减去圆面积就是剪掉的纸屑的面积。
一、单选题
1.世界上第一个把圆周率的值精确到六位小数的数学家是( ??)
A.?刘徽??????????????????????????????????????B.?祖冲之??????????????????????????????????????C.?欧几里德
2.半径是3cm的圆,下列关于这个圆的数据正确的是(??? )
A.?直径9cm????????????????????B.?周长18.84cm????????????????????C.?周长9.42cm????????????????????D.?面积113.04cm2
3.在正方形铁皮上剪下一个圆和一个扇形,恰好围成一个圆锥模型(如右图)。如果圆的半径为r,扇形半径为R,那么R是r的(??? )
A.?6倍???????????????????????????????????????????B.?3倍???????????????????????????????????????????C.?4倍
4.下面三个正方形的边长相等,各图中的阴影部分的面积相比较,(??? )。
A.?图一最大?????????????????????????????B.?图二最大?????????????????????????????C.?图三最大?????????????????????????????D.?一样大
二、判断题
5.直径是3厘米的圆比直径是2厘米的圆的圆周率大.
6.一个圆的周长是它直径的π倍。
7.当圆的半径是2 cm时,它的周长和面积相等。
8.圆周长是直径的3.14倍.
三、填空题
9.圆的公式C=________=________,S=________
10.画一个直径是5厘米的圆,圆规两脚之间的距离是________厘米。如果要画一个周长是12.56厘米的圆,圆规两脚之间的距离应该是________厘米,这个圆的面积是________平方厘米。
11.如图,把一个圆平均分成16份,剪开后拼成一个近似三角形,已知三角形的周长大约是19.14厘米,则圆的面积是________平方厘米。
12.在长8厘米,宽6厘米的长方形里面画一个最大的圆,圆的周长是________厘米,面积是________平方厘米。
13.把一个圆形纸片分成若干等份,然后拼成近似的长方形,量出长方形的长是15.7厘米,这个圆形纸片的面积大约是________。
四、解答题
14.求下图阴影部分的面积。
(1)
(2)
(3)
15.小明在纸上设计了一个图案(图中阴影部分),这个图案的面积是多少?
五、应用题
16.从一张正方形纸上剪下一个周长是18.84厘米的最大圆,求被剪掉的纸屑的面积。
参考答案
一、单选题
1.【答案】 B
【解析】【解答】世界上第一个把圆周率的值精确到六位小数的数学家是祖冲之。
故答案为:B。
【分析】阿基米德是世界上最早进行圆周率计算的,汉朝数学家刘徽将圆周率的值进一步精确了,南北朝数学家祖冲之把π的值精确至小数点后六位,即3.1415926与3.1415927之间,这是当时世界上算得最精确的数值。
2.【答案】 B
【解析】【解答】解:A:直径:3×2=6(cm)。此选项错误;
B:周长:3.14×3×2=18.84(cm)。此选项正确;
C:周长的计算错误;
D:面积:3.14×32=28.26(cm2).此选项错误。
故答案为:B。
【分析】同一个圆内,圆的直径是半径的2倍,圆周长公式:C=2r,圆面积公式:S=, 根据公式计算后选择即可。
3.【答案】 C
【解析】【解答】观察图可得:
2×π×R×=2×π×r
????????? πR=2πr
??? πR÷2π=2πr÷2π
?????????????? =r
?????????? ×4=r×4
???????????????? R=4r
R÷r=4
故答案为:C。
【分析】根据题意可知,小圆的周长等于半径为R的大圆的周长的, 据此列方程,求出R与r的关系。
4.【答案】 D
【解析】【解答】解:三个图中阴影部分的面积都是正方形面积减去一个圆的面积,阴影部分的面积是相等的。
故答案为:D。
【分析】阴影部分的面积都是正方形面积减去空白部分圆的面积,图二空白部分是两个半圆,组合后就是一个整圆;图三空白部分是四个扇形,组合后也是一个圆的面积。
二、判断题
5.【答案】 错误
【解析】【解答】所有圆的圆周率都是一样的,原题说法错误。
故答案为:错误。
【分析】 圆周率指圆的周长与直径的比值,用π表示,圆周率是不变的,据此判断。
6.【答案】正确
【解析】【解答】一个圆的周长是它直径的π倍,此题说法正确.
故答案为:正确.
【分析】根据圆周率的定义可知,圆周率是圆的周长与直径的比值,一般用希腊字母π表示,一个圆的周长是它直径的π倍,据此判断.
7.【答案】 错误
【解析】【解答】解:周长和面积的意义是不同的,无法比较大小。原题说法错误。
故答案为:错误。
【分析】圆的周长是一周的长度,圆的面积是图形的大小,意义不同,单位也不同,面积和周长是无法比较大小的。
8.【答案】 错误
【解析】【解答】圆周长不是直径的3.14倍,说法错误。
故答案为:错误。
【分析】一个圆的周长总是直径的π倍,π约等于3.14,并不等于3.14,所以说:一个圆的周长总是直径的3.14倍是错误的,应该说:一个圆的周长总是直径的π倍。
三、填空题
9.【答案】2πr;πd;πr2
【解析】【解答】解:圆的公式:C=2πr=πd,S=πr?
故答案为:2πr;πd;πr?【分析】圆的周长是直径的π倍,是半径是2π倍,圆的面积是半径的平方乘圆周率,用字母表示这些公式即可。
10.【答案】2.5;2;12.56
【解析】【解答】5÷2=2.5(厘米)
12.56÷2÷3.14
=6.28÷3.14
=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
故答案为:2.5;2;12.56【分析】根据对圆的认识可知,圆规两脚之间的距离是半径,已知圆的直径,求半径,用直径÷2=半径;已知圆的周长,求圆的半径,用公式:C÷2÷π=r,据此列式计算;要求圆的面积,用公式:S=πr2 , 据此列式解答.
11.【答案】 12.56
【解析】【解答】设圆的半径是r,则 ? 8r+=19.14
? ? ?? ? 8r+=19.14
?? ????? 16r+πr=38.28
?????????? 19.14r=38.28
19.14r÷19.14=38.28÷19.14
??????????????????? r=2
圆的面积:
3.14×22
=3.14×4
=12.56(cm2)
故答案为:12.56 。
【分析】观察图可知,把一个圆平均分成16份,剪开后拼成一个近似三角形,设圆的半径是r,三角形的周长=圆的半径×8+圆的周长,据此列方程解答,求出圆的半径,然后用公式:S=πr2 , 据此解答。
12.【答案】 18.84;28.26
【解析】【解答】解:6×3.14=18.84厘米,所以圆的周长是18.84厘米;(6÷2)2×3.14=28.26平方厘米,所以面积是28.26平方厘米。
故答案为:18.84;28.26。
【分析】在一个长方形中画一个最大的圆,这个圆的直径就是长方形的宽,所以圆的周长=圆的直径×π,圆的面积=πr2 , 其中圆的半径=圆的直径÷2。
13.【答案】 25π平方厘米(或78.5平方厘米)
【解析】【解答】解:半径:15.7×2÷3.14÷2=5(厘米)
面积:3.14×52=3.14×25=78.5(平方厘米)
故答案为:78.5平方厘米。
【分析】15.7厘米是圆周长的一半,因此根据圆周长公式先计算出圆的半径,然后根据圆面积公式计算面积。
四、解答题
14.【答案】 (1)解:(10+6)×3÷2-3.14×(6÷2)2÷2=9.87(cm2)
(2)解: ×(52-32)×3.14=12.56(cm2)
(3)解:10÷2=5(dm)
5×5÷2=12.5(dm2)
【解析】【分析】(1)观察图可知,阴影部分的面积=梯形面积-空白半圆的面积,据此列式解答;
(2)观察图可知,阴影部分的面积=圆环的面积×, 据此列式解答;
(3)观察图可知,通过剪拼,可以将两个阴影部分拼成一个底与高都是5dm的直角三角形,根据三角形的面积=底×高÷2,据此列式解答。
15.【答案】 解:3.14×(10÷2)2﹣3.14×(4÷2)2
=3.14×25﹣3.14×4
=78.5﹣12.56
=65.94(平方厘米)
答:阴影部分的面积是65.94平方厘米。
【解析】【分析】从图中可以看出,阴影部分的面积=大圆的面积-小圆的面积,圆的面积=(圆的直径÷2)2×π,据此代入数据作答即可。
五、应用题
16.【答案】解:半径:18.84÷3.14÷2=3(厘米),边长:3×2=6(厘米),
剪掉的面积:
6×6-3.14×3?
=36-28.26
=7.74(平方厘米)
答:被剪掉的纸屑面积是7.74平方厘米。
【解析】【分析】这个圆的直径就是正方形的边长,用圆的周长除以3.14再除以2求出半径,然后计算出正方形的边长,用正方形面积减去圆面积就是剪掉的纸屑的面积。
