北师大版九年级数学上册第一章菱形 矩形难题特训(word 版 含解析)
文档属性
| 名称 | 北师大版九年级数学上册第一章菱形 矩形难题特训(word 版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 15:30:02 | ||
图片预览

文档简介
北师大版九年级数学上册第一章菱形
矩形难题特训解析版
一、选择题(共10题;共30分)
1.如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是(???
)
A.?互相平分???????????????????????????B.?相等?????????????????????????C.?互相垂直???????????????????????????D.?互相垂直平分
2.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.?4???????????????????????????????????????D.?
3.如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为(??
)
A.?????????????????????????????????????B.??????????????????????????????????????C.????????????????????????????????????D.?
4.如图,将矩形纸片
沿
折叠,使点A落在对角线
上的
处.若
,则
等于(??
).
A.??????????????????????????????????????B.???????????????????????????????????????C.??????????????????????????????????????D.?
5.如图,将矩形
折叠,使点C和点A重合,折痕为
,
与
交于点O若
,
,则
的长为(???
)
A.????????????????????????????????????B.?????????????????????????????????????C.??????????????????????????????????????D.?
6.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为(??
)
A.?????????????????????????????????B.??????????????????????????????????C.????????????????????????????????D.?
7.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是(??
)
A.?1???????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
8.如图,菱形纸片ABCD的边长为a,∠ABC=60°,
将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P,若
,则六边形AEFCHG面积的是(?????
)
A.???????????????????????????B.??????????????????????????C.???????????????????????????D.?
9.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P是斜边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,EF与AP相交于点O,则OF的最小值为(???
)
A.?4.8???????????????????????????????????????B.?1.2??????????????????????????????????????C.?3.6????????????????????????????????????????D.?2.4
10.如图,在矩形ABCD中,把矩形ABCD绕点C旋转,得到矩形FEGH,且点E落在AD上,连接BE,BG,交CE于点H,连接FH,若FH平分DEFG,则下列结论:
①
;
②
;
③
;
④
,其中正确的个数是(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(共7题;共28分)
11.如图,在菱形
中,
,点E在
上,若
,则
________.
12.菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=12,菱形ABCD的面积为96,则OE长为________。
13.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=________°。
14.如图,在菱形ABCD中,∠BAD=120°,点E为边AB的中点,点P在对角线BD上,且PE+PA=6,则AB长的最大值为________?。
?
15.如图,将一个矩形纸片ABCD沿着BE折叠,使点C、D分别落在点C、D处,若∠ABC=70°,则∠ABE的度数是________度。
16.如图是一张矩形纸片ABCD,已知AB=8,AD=6,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在矩形ABCD的某一条边上,则等腰三角形AEP的底边上的高的长是________.
17.如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长为________..
三、解答题一(共3题;共18分)
18.如图,
的对角线AC,BD相交于点O,过点O作
,分别交AB,DC于点E、F,连接AF、CE.
(1)若
,求EF的长;
(2)判断四边形AECF的形状,并说明理由.
19.如图,在△ABC中,AB=AC
,
点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F
,
连接CF
.
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
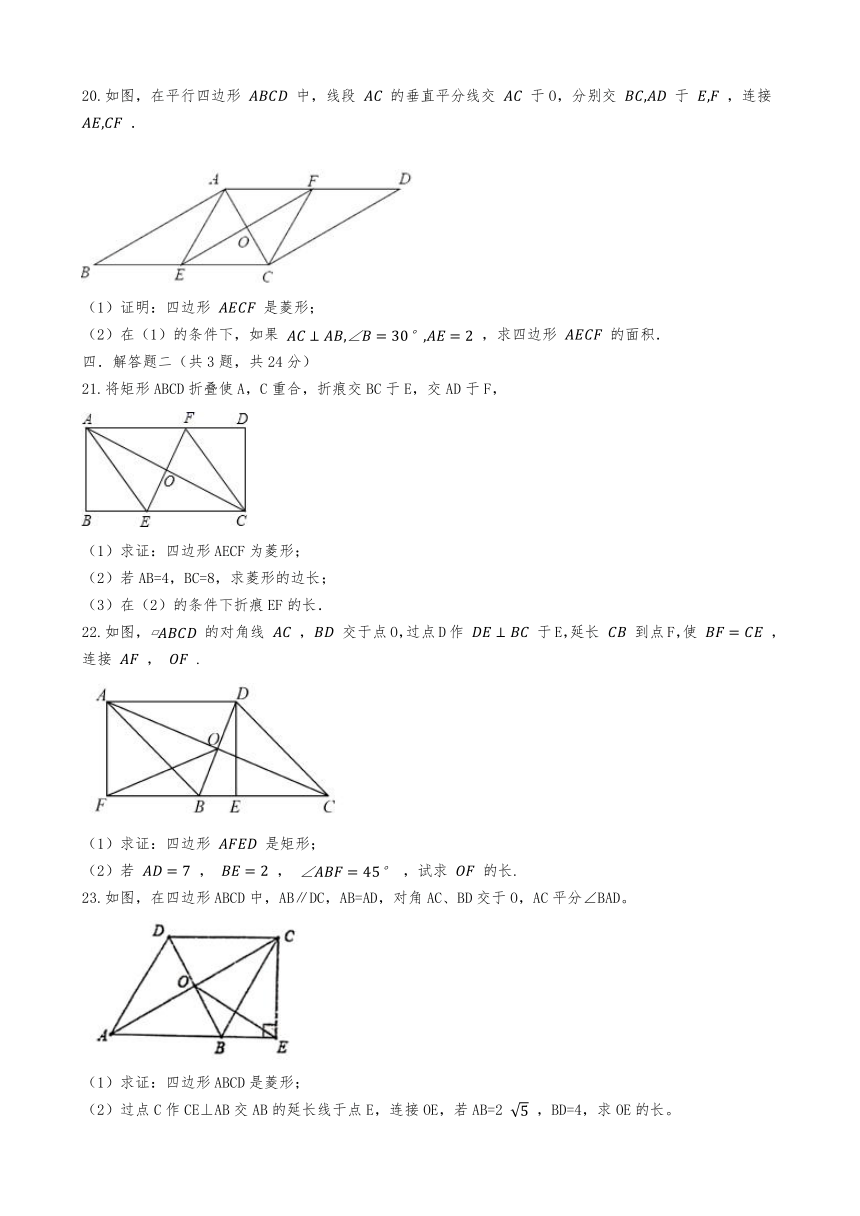
20.如图,在平行四边形
中,线段
的垂直平分线交
于O,分别交
于
,连接
.
(1)证明:四边形
是菱形;
(2)在(1)的条件下,如果
,求四边形
的面积.
四.解答题二(共3题,共24分)
21.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
22.如图,
的对角线
,
交于点O,过点D作
于E,延长
到点F,使
,连接
,
.
(1)求证:四边形
是矩形;
(2)若
,
,
,试求
的长.
23.如图,在四边形ABCD中,AB∥DC,AB=AD,对角AC、BD交于O,AC平分∠BAD。
(1)求证:四边形ABCD是菱形;
(2)过点C作CE⊥AB交AB的延长线于点E,连接OE,若AB=2
,BD=4,求OE的长。
五.解答题三(共2题,共20分)
24.如图,已知矩形ABCD中,∠ACB=30°,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B′落在AC上,B′C′交AD于点E,在B′C′上取点F,使FB′=AB。
(1)求证:BB′=FB′;
(2)求∠FBB′的度数;
(3)已知AB=4,求△BFB′面积。
25.如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
答案
一、选择题
1.根据题意画出图形如下:
答:AC与BD
的位置关系是互相垂直.
证明:∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故答案为:C.
2.解:如图.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,OA=
AC=3,BD=2OB,
∵AB=5,
∴OB=
=4,
∴BD=2OB=8,
∵S菱形ABCD=AB?DE=
AC?BD,
∴DE=
=
=
.
故答案为:D.
3.解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,S=
AC×BD,
∵EF⊥BD于F,EG⊥AC于G,
∴四边形EFOG是矩形,EF∥OC,EG∥OB,
∵点E是线段BC的中点,
∴EF、EG都是△OBC的中位线,
∴EF=
OC=
AC,EG=
OB=
BD,
∴矩形EFOG的面积=EF×EG=
AC×
BD=
=
S;
故答案为:B.
4.∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABD=90°-
=66°,
∵将矩形纸片
沿
折叠,使点
落在对角线
上的
处,
∴∠EBA’=
∠ABD
=33°,
∴
=90°-∠EBA’=
,
故答案为:C.
5.解:由对折可得:
?矩形
,
?
?
?
?
BC=8
?
由对折得:
故答案为:C.
6.由折叠补全图形如图所示,
∵四边形ABCD是矩形,
∴∠ADA'=∠B=∠C=∠A=90°,AD=BC=1,CD=AB
,
由第一次折叠得:∠DAE=∠A=90°,∠ADE=
∠ADC=45°,
∴∠AED=∠ADE=45°,
∴AE=AD=1,
在Rt△ADG中,根据勾股定理得,DE=
AD=
,
故答案为:
A
.
7.解:根据题意可知菱形
的高等于
的一半,
菱形
的面积为
,正方形
的面积为
.
菱形
的面积与正方形
的面积之比是
.
故答案为:B.
8.解:∵
菱形纸片ABCD的边长为a,∠ABC=60°
,
菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P
,
∴△BEF,△DGH,△ABC为等边三角形,
∵AE=2BE,∴BG=2AG,
∴BE=a,BG=,
∴△BEF的面积=
,
△DGH的面积=,
△ABC面积=
,
∴
六边形AEFCHG面积=菱形ABCD面积-△BEF的面积-△DGH的面积
=2△ABC面积-△BEF的面积-△DGH的面积=.
故答案为:C.
9.解:∵四边形AEPF为矩形
∴EF和AP互相平分,且EF=AP,OE=OF
∵当AP的值最小时,AM的值最小
∴当AP⊥BC时,AP的值最小,即OF的值最小
∵AP×BC=AB×AC
∴AP×BC=AB×AC
在直角三角形ABC中,由勾股定理得,BC==10
∵AB=6,AC=8
∴10AP=6×8
∴AP=
∴OF=EF=
故答案为:D.
10.解:如图,作BM⊥EC于M.
?
∵CB=CE,
∴∠CBE=∠CEB,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠AEB=∠MEB,
∵∠A=∠BME=90°,BE=BE,
∴△BEA≌△BEM(AAS),
∴AE=EM,AB=BM.
∵∠BMH=∠GCH=90°,∠BHM=∠GHC,BM=AB=CG,
∴△BMH≌△GCH(AAS),
∴MH=CH,BH=HG,
∴EH=EM+MH=AE+CH,故①③符合题意,
∵∠AEB+∠ABE=90°,
∴2∠AEB+2∠ABE=180°,
∵∠DEC+∠AEC=180°,∠AEC=2∠AEB,
∴∠DEC+2∠AEB=180°,
∴∠DEC=2∠ABE,故②符合题意,
∵FH平分∠EFG,
∴∠EFH=45°,
∵∠FEH=90°,
∴AB=EF=EH,
∵EH>HM=CH,
∴CH<AB,故④不符合题意.
故答案为:C.
二、填空题
11.解:四边形ABCD是菱形,
,
∴AB∥CD,
∴∠BCD=180°-∠B=130°,∠ACE=
∠BCD=65°,
∵
,
∴∠ACE=∠AEC=65°,
∴∠BAE=180°-∠AEC=115°.
12.解:四边形ABCD为菱形,AC=12,菱形ABCD的面积为96
∴S菱形ABCD=×AC×BD=×12DB=96
解得,BD=16
∴AO=OC=6,OB=OD=8,AO⊥BO,又∵点E为AB的中点
∴OE为△DAB的中位线
在直角三角形AOB中,AB==10
∴OE=AD=AB=5
13.解:在矩形ABCD中
∵∠AOD=110°
∴∠DOC=180°-110°=70°
∵四边形ABCD为矩形
∴OD=OC
∴∠OCD=∠CDO=(180°-70°)÷2=55°
在直角三角形DEC中,∠CDE=90°-55°=35°
14.解:连接PC,CE,AC,如图
∵四边形ABCD为菱形
∴AB=BC,直线BD为菱形ABCD的对称轴
∴AP=PC
∴CE≤PE+PC=PE+PA=6
∵∠DAB=120°
∴∠ABC=60°
∴△ABC为等边三角形,
∵点E为线段AB的中点
∴AE=BE,CE⊥AB
∴∠AEC=90°
∴∠BCE=30°
∴BE=BC
∴CE==BC=AB≤6
∴AB≤4
∴AB的最大值为4
15.解:根据折叠的性质得∠CBE=∠C′BE,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ABC′=70°,
∴∠CBC′=90°+70°=160°,
∴∠BCE=80°,
∴∠ABE=90°-80°=10°.
16.解:①当AP=AE=5时,如图所示:过点A作AH⊥PE于H,
∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=
AE=5
,
∵AH⊥PE,△AEP是等腰直角三角形,
∴AH=
PE=
;
②当P'E=AE=5时,
∵BE=AB﹣AE=8﹣5=3,∠B=90°,
∴P'B=
=4,
∴底边AP'=
=
=4
,
∵tan∠P'AB=
,
∴
,
∴ME=
;
③当P''A=P''E时,
∵AB∥CD,
∴底边AE的高为AD=6;
综上所述:等腰三角形AEP的底边上的高的长是
或
或6.
故答案为:
或
或6.
17.
解:∵四边形ABCD为矩形,
∴∠BAD=90°,OB=OD,AC=BD,
又∵OF⊥AD,
∴OF∥AB,
又∵OB=OD
,
∴
AB=2OF=4cm,
∵BE︰BD=1︰4,
∴BE︰ED=1︰3
设BE=x,ED=3x
,
则BD=4
x
,
∵AE⊥BD于点E
∴
,
∴16-x2=AD2-9x2
又∵AD2=BD2-AB2=16
x2-16
,
∴16-x2=16
x2-16-9x2
,
8x2=32
∴x2=4,
∴x=2
∴BD=2×4=8(cm),
∴AC=8cm
.
故答案为:AC=8cm
.
解答题一
18.
(1)解:∵四边形ABCD是平行四边形,AC、BD是对角线,
∴
,OA=OC,
又∵
,
∴
,
在△AOE和△COF中,
,
∴
.
∴FO=EO,
又∵
,
∴
.
故EF的长为3.
(2)解:由(1)可得,
,四边形ABCD是平行四边形,
∴
,FC∥AE,
∴四边形AECF是平行四边形,
又
,OE=OF,OA=OC,
∴平行四边形AECF是菱形.
19.(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是线段AD的中点,
∴AE=DE,
∵∠AEF=∠DEB,
∴
(AAS);
(2)证明:∵
,
∴AF=BD,
∵D是线段BC的中点,
∴BD=CD,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵AB=AC,
∴
,
∴∠ADC=90°,
∴四边形ADCF为矩形.
20.(1)解:
是线段
的垂直平分线
,
是等腰三角形
(等腰三角形的三线合一)
四边形
是平行四边形
四边形
是菱形;
(2)解:
,即
四边形
是菱形,
,
在
中,
,
即四边形
的面积为
.
四.解答题二
21.(1)证明:∵矩形ABCD折叠使A,C重合,折痕为EF,∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,∴∠FAC=∠ECA,在△AOF和△COE中,
,∴△AOF≌△COE,
∴OF=OE,∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)解:设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2
,
∴(8﹣x)2+42=x2
,
解得x=5,
即菱形的边长为5;
(3)解:在Rt△ABC中,AC=
=
=4
,
∴OA=
AC=2
,
在Rt△AOE中,OE=
=
=
,
∴EF=2OE=2
.
22.
(1)证明:
是平行四边形,
,
.
,
.
∴
四边形
是平行四边形.
,
.
四边形
是矩形;
(2)解:由(1)得
,
,
,
,
,
,
.
,
.
在
中,由勾股定理,得
.
是平行四边形,
.
.
23.
(1)解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=4,
∴OB=
BD=2,
在Rt△AOB中,AB=2
,OB=2,
∴OA=
=
=4,
∴OE=OA=4.
解答题三
24.
(1)证明:∵矩形ABCD中,∠ACB=30°
∴∠BAC=60°
由旋转可得:AB′=AB
∴△ABB′为等边三角形,
∴BB′=AB
∵FB′=AB
∴BB′=FB
(2)解:由(1)得到△ABB′为等边三角形,
∴∠AB′B=60°,
由旋转可得∠AB′F=90°
∴∠BB′F=150°
∴BB′=FB′
∴∠FBB′=∠BFB′=15
(3)解:过B作BH⊥BF交FB′的延长线于H,
∵∠FBB′=∠BFB′=15°
∴∠BB′H=30°
在Rt△BB′H中,BB′=AB=4,∠BB′H=30°
∴BH=2
S△OCN=
,
?
25.
(1)解:H(2,4)
∵A(0,4),C(6,0),四边形OCBA为矩形,
OA=BC=4,AB=OC=6
∵α=45°,∠ABC=90°,
△HBC是等腰直角三角形,BH=BC=4,
AH=AB-BH=6-4=2,
H(2,4).
(2)解:△CBD为等边三角形
∵α=60°,
∠BCD=∠α=60°
又∵BC=DC,
△CBD为等边三角形
(3)解:设AH=CH=x,则在RtΔBCH中由勾股定理可得x2=(6-x)2+42,解得x=
.故H(
,4).
设HC:y=kx+b(k≠0),则有
解得
∴直线HC的解析式为y=-
x+
.
矩形难题特训解析版
一、选择题(共10题;共30分)
1.如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是(???
)
A.?互相平分???????????????????????????B.?相等?????????????????????????C.?互相垂直???????????????????????????D.?互相垂直平分
2.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.?4???????????????????????????????????????D.?
3.如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为(??
)
A.?????????????????????????????????????B.??????????????????????????????????????C.????????????????????????????????????D.?
4.如图,将矩形纸片
沿
折叠,使点A落在对角线
上的
处.若
,则
等于(??
).
A.??????????????????????????????????????B.???????????????????????????????????????C.??????????????????????????????????????D.?
5.如图,将矩形
折叠,使点C和点A重合,折痕为
,
与
交于点O若
,
,则
的长为(???
)
A.????????????????????????????????????B.?????????????????????????????????????C.??????????????????????????????????????D.?
6.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为(??
)
A.?????????????????????????????????B.??????????????????????????????????C.????????????????????????????????D.?
7.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是(??
)
A.?1???????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
8.如图,菱形纸片ABCD的边长为a,∠ABC=60°,
将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P,若
,则六边形AEFCHG面积的是(?????
)
A.???????????????????????????B.??????????????????????????C.???????????????????????????D.?
9.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P是斜边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,EF与AP相交于点O,则OF的最小值为(???
)
A.?4.8???????????????????????????????????????B.?1.2??????????????????????????????????????C.?3.6????????????????????????????????????????D.?2.4
10.如图,在矩形ABCD中,把矩形ABCD绕点C旋转,得到矩形FEGH,且点E落在AD上,连接BE,BG,交CE于点H,连接FH,若FH平分DEFG,则下列结论:
①
;
②
;
③
;
④
,其中正确的个数是(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(共7题;共28分)
11.如图,在菱形
中,
,点E在
上,若
,则
________.
12.菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=12,菱形ABCD的面积为96,则OE长为________。
13.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=________°。
14.如图,在菱形ABCD中,∠BAD=120°,点E为边AB的中点,点P在对角线BD上,且PE+PA=6,则AB长的最大值为________?。
?
15.如图,将一个矩形纸片ABCD沿着BE折叠,使点C、D分别落在点C、D处,若∠ABC=70°,则∠ABE的度数是________度。
16.如图是一张矩形纸片ABCD,已知AB=8,AD=6,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在矩形ABCD的某一条边上,则等腰三角形AEP的底边上的高的长是________.
17.如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长为________..
三、解答题一(共3题;共18分)
18.如图,
的对角线AC,BD相交于点O,过点O作
,分别交AB,DC于点E、F,连接AF、CE.
(1)若
,求EF的长;
(2)判断四边形AECF的形状,并说明理由.
19.如图,在△ABC中,AB=AC
,
点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F
,
连接CF
.
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
20.如图,在平行四边形
中,线段
的垂直平分线交
于O,分别交
于
,连接
.
(1)证明:四边形
是菱形;
(2)在(1)的条件下,如果
,求四边形
的面积.
四.解答题二(共3题,共24分)
21.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
22.如图,
的对角线
,
交于点O,过点D作
于E,延长
到点F,使
,连接
,
.
(1)求证:四边形
是矩形;
(2)若
,
,
,试求
的长.
23.如图,在四边形ABCD中,AB∥DC,AB=AD,对角AC、BD交于O,AC平分∠BAD。
(1)求证:四边形ABCD是菱形;
(2)过点C作CE⊥AB交AB的延长线于点E,连接OE,若AB=2
,BD=4,求OE的长。
五.解答题三(共2题,共20分)
24.如图,已知矩形ABCD中,∠ACB=30°,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B′落在AC上,B′C′交AD于点E,在B′C′上取点F,使FB′=AB。
(1)求证:BB′=FB′;
(2)求∠FBB′的度数;
(3)已知AB=4,求△BFB′面积。
25.如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
答案
一、选择题
1.根据题意画出图形如下:
答:AC与BD
的位置关系是互相垂直.
证明:∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故答案为:C.
2.解:如图.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,OA=
AC=3,BD=2OB,
∵AB=5,
∴OB=
=4,
∴BD=2OB=8,
∵S菱形ABCD=AB?DE=
AC?BD,
∴DE=
=
=
.
故答案为:D.
3.解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,S=
AC×BD,
∵EF⊥BD于F,EG⊥AC于G,
∴四边形EFOG是矩形,EF∥OC,EG∥OB,
∵点E是线段BC的中点,
∴EF、EG都是△OBC的中位线,
∴EF=
OC=
AC,EG=
OB=
BD,
∴矩形EFOG的面积=EF×EG=
AC×
BD=
=
S;
故答案为:B.
4.∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABD=90°-
=66°,
∵将矩形纸片
沿
折叠,使点
落在对角线
上的
处,
∴∠EBA’=
∠ABD
=33°,
∴
=90°-∠EBA’=
,
故答案为:C.
5.解:由对折可得:
?矩形
,
?
?
?
?
BC=8
?
由对折得:
故答案为:C.
6.由折叠补全图形如图所示,
∵四边形ABCD是矩形,
∴∠ADA'=∠B=∠C=∠A=90°,AD=BC=1,CD=AB
,
由第一次折叠得:∠DAE=∠A=90°,∠ADE=
∠ADC=45°,
∴∠AED=∠ADE=45°,
∴AE=AD=1,
在Rt△ADG中,根据勾股定理得,DE=
AD=
,
故答案为:
A
.
7.解:根据题意可知菱形
的高等于
的一半,
菱形
的面积为
,正方形
的面积为
.
菱形
的面积与正方形
的面积之比是
.
故答案为:B.
8.解:∵
菱形纸片ABCD的边长为a,∠ABC=60°
,
菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P
,
∴△BEF,△DGH,△ABC为等边三角形,
∵AE=2BE,∴BG=2AG,
∴BE=a,BG=,
∴△BEF的面积=
,
△DGH的面积=,
△ABC面积=
,
∴
六边形AEFCHG面积=菱形ABCD面积-△BEF的面积-△DGH的面积
=2△ABC面积-△BEF的面积-△DGH的面积=.
故答案为:C.
9.解:∵四边形AEPF为矩形
∴EF和AP互相平分,且EF=AP,OE=OF
∵当AP的值最小时,AM的值最小
∴当AP⊥BC时,AP的值最小,即OF的值最小
∵AP×BC=AB×AC
∴AP×BC=AB×AC
在直角三角形ABC中,由勾股定理得,BC==10
∵AB=6,AC=8
∴10AP=6×8
∴AP=
∴OF=EF=
故答案为:D.
10.解:如图,作BM⊥EC于M.
?
∵CB=CE,
∴∠CBE=∠CEB,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠AEB=∠MEB,
∵∠A=∠BME=90°,BE=BE,
∴△BEA≌△BEM(AAS),
∴AE=EM,AB=BM.
∵∠BMH=∠GCH=90°,∠BHM=∠GHC,BM=AB=CG,
∴△BMH≌△GCH(AAS),
∴MH=CH,BH=HG,
∴EH=EM+MH=AE+CH,故①③符合题意,
∵∠AEB+∠ABE=90°,
∴2∠AEB+2∠ABE=180°,
∵∠DEC+∠AEC=180°,∠AEC=2∠AEB,
∴∠DEC+2∠AEB=180°,
∴∠DEC=2∠ABE,故②符合题意,
∵FH平分∠EFG,
∴∠EFH=45°,
∵∠FEH=90°,
∴AB=EF=EH,
∵EH>HM=CH,
∴CH<AB,故④不符合题意.
故答案为:C.
二、填空题
11.解:四边形ABCD是菱形,
,
∴AB∥CD,
∴∠BCD=180°-∠B=130°,∠ACE=
∠BCD=65°,
∵
,
∴∠ACE=∠AEC=65°,
∴∠BAE=180°-∠AEC=115°.
12.解:四边形ABCD为菱形,AC=12,菱形ABCD的面积为96
∴S菱形ABCD=×AC×BD=×12DB=96
解得,BD=16
∴AO=OC=6,OB=OD=8,AO⊥BO,又∵点E为AB的中点
∴OE为△DAB的中位线
在直角三角形AOB中,AB==10
∴OE=AD=AB=5
13.解:在矩形ABCD中
∵∠AOD=110°
∴∠DOC=180°-110°=70°
∵四边形ABCD为矩形
∴OD=OC
∴∠OCD=∠CDO=(180°-70°)÷2=55°
在直角三角形DEC中,∠CDE=90°-55°=35°
14.解:连接PC,CE,AC,如图
∵四边形ABCD为菱形
∴AB=BC,直线BD为菱形ABCD的对称轴
∴AP=PC
∴CE≤PE+PC=PE+PA=6
∵∠DAB=120°
∴∠ABC=60°
∴△ABC为等边三角形,
∵点E为线段AB的中点
∴AE=BE,CE⊥AB
∴∠AEC=90°
∴∠BCE=30°
∴BE=BC
∴CE==BC=AB≤6
∴AB≤4
∴AB的最大值为4
15.解:根据折叠的性质得∠CBE=∠C′BE,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ABC′=70°,
∴∠CBC′=90°+70°=160°,
∴∠BCE=80°,
∴∠ABE=90°-80°=10°.
16.解:①当AP=AE=5时,如图所示:过点A作AH⊥PE于H,
∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=
AE=5
,
∵AH⊥PE,△AEP是等腰直角三角形,
∴AH=
PE=
;
②当P'E=AE=5时,
∵BE=AB﹣AE=8﹣5=3,∠B=90°,
∴P'B=
=4,
∴底边AP'=
=
=4
,
∵tan∠P'AB=
,
∴
,
∴ME=
;
③当P''A=P''E时,
∵AB∥CD,
∴底边AE的高为AD=6;
综上所述:等腰三角形AEP的底边上的高的长是
或
或6.
故答案为:
或
或6.
17.
解:∵四边形ABCD为矩形,
∴∠BAD=90°,OB=OD,AC=BD,
又∵OF⊥AD,
∴OF∥AB,
又∵OB=OD
,
∴
AB=2OF=4cm,
∵BE︰BD=1︰4,
∴BE︰ED=1︰3
设BE=x,ED=3x
,
则BD=4
x
,
∵AE⊥BD于点E
∴
,
∴16-x2=AD2-9x2
又∵AD2=BD2-AB2=16
x2-16
,
∴16-x2=16
x2-16-9x2
,
8x2=32
∴x2=4,
∴x=2
∴BD=2×4=8(cm),
∴AC=8cm
.
故答案为:AC=8cm
.
解答题一
18.
(1)解:∵四边形ABCD是平行四边形,AC、BD是对角线,
∴
,OA=OC,
又∵
,
∴
,
在△AOE和△COF中,
,
∴
.
∴FO=EO,
又∵
,
∴
.
故EF的长为3.
(2)解:由(1)可得,
,四边形ABCD是平行四边形,
∴
,FC∥AE,
∴四边形AECF是平行四边形,
又
,OE=OF,OA=OC,
∴平行四边形AECF是菱形.
19.(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是线段AD的中点,
∴AE=DE,
∵∠AEF=∠DEB,
∴
(AAS);
(2)证明:∵
,
∴AF=BD,
∵D是线段BC的中点,
∴BD=CD,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵AB=AC,
∴
,
∴∠ADC=90°,
∴四边形ADCF为矩形.
20.(1)解:
是线段
的垂直平分线
,
是等腰三角形
(等腰三角形的三线合一)
四边形
是平行四边形
四边形
是菱形;
(2)解:
,即
四边形
是菱形,
,
在
中,
,
即四边形
的面积为
.
四.解答题二
21.(1)证明:∵矩形ABCD折叠使A,C重合,折痕为EF,∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,∴∠FAC=∠ECA,在△AOF和△COE中,
,∴△AOF≌△COE,
∴OF=OE,∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)解:设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2
,
∴(8﹣x)2+42=x2
,
解得x=5,
即菱形的边长为5;
(3)解:在Rt△ABC中,AC=
=
=4
,
∴OA=
AC=2
,
在Rt△AOE中,OE=
=
=
,
∴EF=2OE=2
.
22.
(1)证明:
是平行四边形,
,
.
,
.
∴
四边形
是平行四边形.
,
.
四边形
是矩形;
(2)解:由(1)得
,
,
,
,
,
,
.
,
.
在
中,由勾股定理,得
.
是平行四边形,
.
.
23.
(1)解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=4,
∴OB=
BD=2,
在Rt△AOB中,AB=2
,OB=2,
∴OA=
=
=4,
∴OE=OA=4.
解答题三
24.
(1)证明:∵矩形ABCD中,∠ACB=30°
∴∠BAC=60°
由旋转可得:AB′=AB
∴△ABB′为等边三角形,
∴BB′=AB
∵FB′=AB
∴BB′=FB
(2)解:由(1)得到△ABB′为等边三角形,
∴∠AB′B=60°,
由旋转可得∠AB′F=90°
∴∠BB′F=150°
∴BB′=FB′
∴∠FBB′=∠BFB′=15
(3)解:过B作BH⊥BF交FB′的延长线于H,
∵∠FBB′=∠BFB′=15°
∴∠BB′H=30°
在Rt△BB′H中,BB′=AB=4,∠BB′H=30°
∴BH=2
S△OCN=
,
?
25.
(1)解:H(2,4)
∵A(0,4),C(6,0),四边形OCBA为矩形,
OA=BC=4,AB=OC=6
∵α=45°,∠ABC=90°,
△HBC是等腰直角三角形,BH=BC=4,
AH=AB-BH=6-4=2,
H(2,4).
(2)解:△CBD为等边三角形
∵α=60°,
∠BCD=∠α=60°
又∵BC=DC,
△CBD为等边三角形
(3)解:设AH=CH=x,则在RtΔBCH中由勾股定理可得x2=(6-x)2+42,解得x=
.故H(
,4).
设HC:y=kx+b(k≠0),则有
解得
∴直线HC的解析式为y=-
x+
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
