第二章 直角三角形的边角关系 章末复习(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 章末复习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
章末复习
知识构建
考点训练
考点1 锐角三角函数的变换规律
1.如图所示,已知45°<∠A<90°,则下列各式成立的是( )
A. sinA =cosA
B. sinA> cosA
C. sinA>tanA
D. sinA<cosA
2.比较下列三角函数值的大小
(1)tan36°_______ tan55?;
(2)sin40°_______ cos40°。
考点2 根据30°,45°,60°角的三角函数值求相应锐角的大小
3.在Rt△ABC中,∠C=90°,若sinA=,则∠A的度数是( )
A. 60° B. 45° C. 30° D. 无法确定
4.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A=____________。
5.设∠A是锐角,如果sin(A-20°)=,则∠A的度数是___________。
6.在△ABC中,∠C=90°,若cosB=,则sinA的值为___________。
考点3 化斜为直,解三角形
7.如图所示,在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积.(结果保留根号)
8.如图所示,在△ABC中,∠A=30°,AC=4,AB=3,求BC的长.
考点4 锐角三角函数的实际应用
9.如图所示,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米,上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度.(精确到0.1米.参考数据:≈1.73)
10.(2019·鄂州)为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如图所示小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A,B,D,E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行。
(1)求点F到直线CE的距离(结果保留根号);
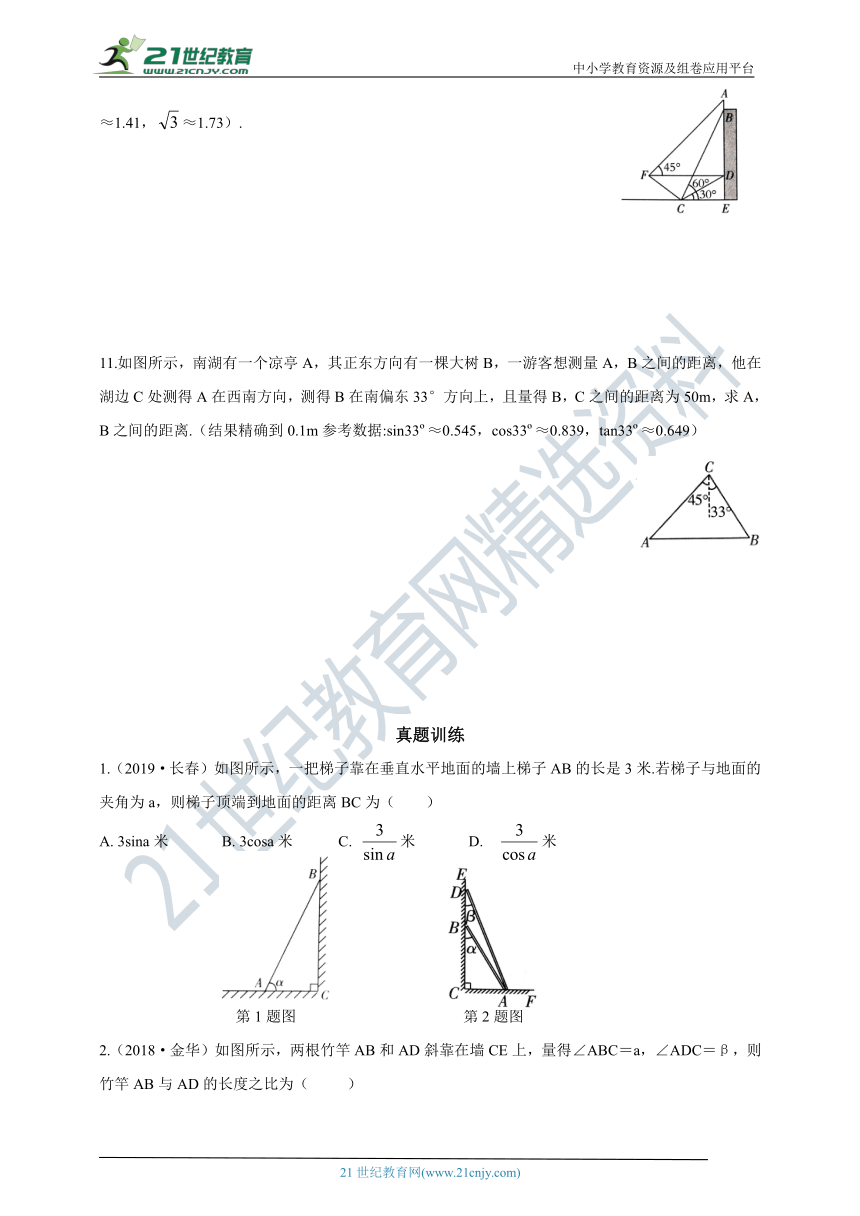
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).
11.如图所示,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A,B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B,C之间的距离为50m,求A,B之间的距离.(结果精确到0.1m参考数据:sin33?≈0.545,cos33?≈0.839,tan33?≈0.649)
真题训练
1.(2019·长春)如图所示,一把梯子靠在垂直水平地面的墙上梯子AB的长是3米.若梯子与地面的夹角为a,则梯子顶端到地面的距离BC为( )
A. 3sina米 B. 3cosa米 C. 米 D. 米
第1题图 第2题图
2.(2018·金华)如图所示,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=a,∠ADC=β,则竹竿AB与AD的长度之比为( )
A. B. C. D.
3.(2019·威海)如图所示,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点,已知坡角为20°,山高BC=2千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
第3题图 第4题图
4.(2018·长春)如图所示,某地要修建高速公路,要从A地向B地修一条隧道(点A,B在同一
水平面上)为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为a,则A,B两地之间的距离为( )
800sina米 B. 800tana米 C. 米 D. 米
5.(2019·营口)如图所示,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
第5题图 第6题图
6.(2019·泰安)如图所示,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为________km( )
A.30+30 B.30+10 C.10+30 D.30
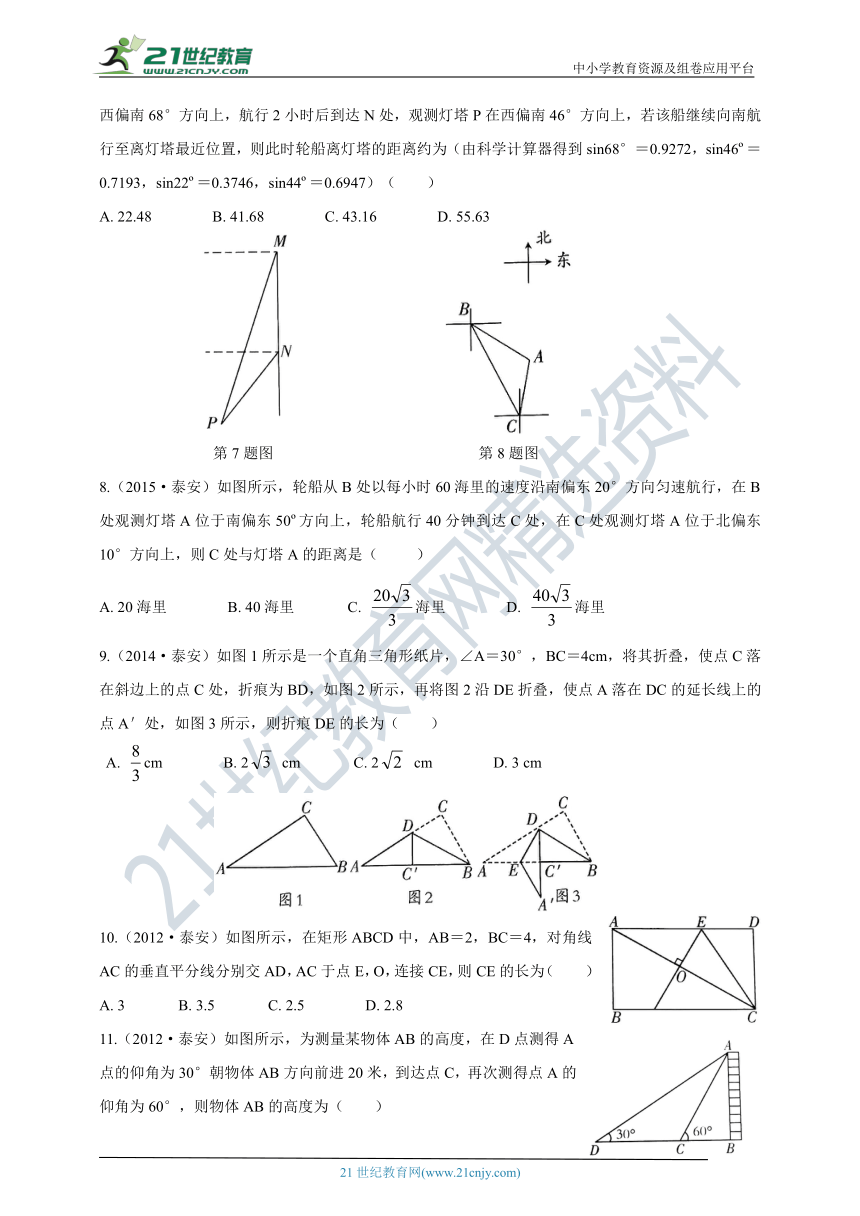
7.(2016·泰安)如图所示,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46?=0.7193,sin22?=0.3746,sin44?=0.6947)( )
A. 22.48 B. 41.68 C. 43.16 D. 55.63
第7题图 第8题图
8.(2015·泰安)如图所示,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50?方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A. 20海里 B. 40海里 C. 海里 D. 海里
9.(2014·泰安)如图1所示是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图2所示,再将图2沿DE折叠,使点A落在DC的延长线上的点A'处,如图3所示,则折痕DE的长为( )
A. cm B. 2 cm C. 2 cm D. 3 cm
10.(2012·泰安)如图所示,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( )
A. 3 B. 3.5 C. 2.5 D. 2.8
11.(2012·泰安)如图所示,为测量某物体AB的高度,在D点测得A点的仰角为30°朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A. 10米 B. 10米 C. 20米 D.米
12.(2018·广西)如图所示,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120 m,则乙楼的高CD是_________ m.(结果保留根号)
第12题图 第13题图
13.(2018·泰安)如图所示,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA′的延长线恰好过点C,则sin∠ABE的值为 _________。
14.(2013·泰安)如图所示,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为_______海里(取≈1.7,结果精确到0.1海里)
15.(2019·邵阳)某品牌太阳能热水器的实物图和横断面示意图如图所示.已知真空集热管DE与支架CB所在直线相交于点O,且OB=OE;支架BC与水平线AD垂直,AC=40 cm,∠ADE=30°,DE=190 cm,另一支架AB与水平线夹角∠BAD=65°,求OB的长度.(结果精确到1cm;温馨提示:sin65?≈0.91,cos65°≈0.42,tan65?≈2.14)
16.(2019·郴州)如图所示,巡逻船在A处测得灯塔C在北偏东45°方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东60°方向上,这时巡逻船与渔船的距离是多少?(精确到0.01 km.参考数据:≈1.414,≈1.732,≈2.449)
参考答案
知识构建
① ② ③ ④ ⑤1 ⑥ ⑦∠A+∠B=90°
⑧除直角外的两个条件,其中至少一个是边
考点训练
B 2.(1)< (2)< 3. C 4. 30° 5. 80° 6.
7,解:如图所示,过点C作CD⊥AB于点D.
∵∠A=60?,∠B=45?,∴∠ACD=30?。∠BCD=∠B=45?.
∴CD=AD?tanA,BD=CD.设AD=X,则CD=x·tan60?=x=8,
∵AB=AD+BD=x+x=8,∴x=4(-1).
∴CD=x=12-4.
∴S△ABC =AB·CD=×8×(12-4)=48-16.
8,解:如图所示,过点C作CD上AB于点D.
在Rt△ACD中,∠A=30?,AC=4.∴CD=2,AD=2.
∵AB=3,∴BD=.∴BC=。
9,解:设每层楼高为x米,
由题意得,MC'=MC-CC'=2. 5-1.5=1(米),
∴DC'=5x+1(米), EC'=4x+1(米).
在Rt△DC'A'中,∠DA'C'=60?,∴C'A'=米.
在Rt△EC'B'中,∠EB'C'=30°,∴C'B'==米。
∵A'B'=C'B'-C'A'=AB,∴-=14.解得x≈3.17.
∴5x+2.5≈18.4.
答:居民楼高约为18.4米.
10,解:(1)如图所示,过点F作FG⊥EC于点G。
由题意得,∠FDE=∠DEG=∠FGE=90°∴四边形DEGF是矩形,∴FG=DE.
在Rt△CDE中,DE=CE·tan∠DCE=2(米);∴点F到地面的距离为2米;
(2)∵坡度i=1:1.5,∴在Rt△CFG中,CG=1.5FG=3(米)∴FD=EG=3+6(米).
∵∠ADF=90°,∠AFD=45°,∴AD=DF=3+6(米).
在Rt△BCE中,BE=CE·tan∠BCE=6(米),
∴AB=AD+DE-BE=3+6+2-6=6-≈4.3(米)
答:宣传牌的高度约为4.3米.
11,解:如图所示,过点C作CD⊥AB于点D。
在Rt△BCD中,∵∠BDC=90°,sin33°=,∴BD=50×sin33?≈27.25(m)
∵cos33°=,∴CD=50×cos33°≈41.95(m).
∵∠ACD=45°,CD⊥AB,∴AD=CD=41.95(m)
∴AB=AD+BD=41.95+27.25=69.2(m)
答:A,B之间的距离约为69.2m.
真题训练
A 2. B 3. A 4. D 5. C 6. B 7. B 8. D 9. A 10. C 11. A 12. 40 13. 14. 67.5
15.解:设OE=OB=2x,∴OD=DE+OE=190+2x.
∵∠ADE=30°,∴OC=OD=95+x.∴BC=OC-OB=95+x-2x=95-x.
∵tan∠BAD=,∴2.14=,解得x=9.4.∴OB=2x≈19(cm).
答:OB的长度为19cm。
16.解:如图所示,延长CB交AD于点D,则∠CDA=90°。
在Rt△ADC中,AC=30(km),∠CAD=45?,∴AD=CD=AC=15(km)。
在Rt△ADB中,AD=15(km),∠BAD=30°,∴AB==10≈24.49(km)
答:巡逻船与渔船的距离约为24.49km
_21?????????è?????(www.21cnjy.com)_
第二章 直角三角形的边角关系
章末复习
知识构建
考点训练
考点1 锐角三角函数的变换规律
1.如图所示,已知45°<∠A<90°,则下列各式成立的是( )
A. sinA =cosA
B. sinA> cosA
C. sinA>tanA
D. sinA<cosA
2.比较下列三角函数值的大小
(1)tan36°_______ tan55?;
(2)sin40°_______ cos40°。
考点2 根据30°,45°,60°角的三角函数值求相应锐角的大小
3.在Rt△ABC中,∠C=90°,若sinA=,则∠A的度数是( )
A. 60° B. 45° C. 30° D. 无法确定
4.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A=____________。
5.设∠A是锐角,如果sin(A-20°)=,则∠A的度数是___________。
6.在△ABC中,∠C=90°,若cosB=,则sinA的值为___________。
考点3 化斜为直,解三角形
7.如图所示,在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积.(结果保留根号)
8.如图所示,在△ABC中,∠A=30°,AC=4,AB=3,求BC的长.
考点4 锐角三角函数的实际应用
9.如图所示,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米,上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度.(精确到0.1米.参考数据:≈1.73)
10.(2019·鄂州)为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如图所示小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A,B,D,E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行。
(1)求点F到直线CE的距离(结果保留根号);
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).
11.如图所示,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A,B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B,C之间的距离为50m,求A,B之间的距离.(结果精确到0.1m参考数据:sin33?≈0.545,cos33?≈0.839,tan33?≈0.649)
真题训练
1.(2019·长春)如图所示,一把梯子靠在垂直水平地面的墙上梯子AB的长是3米.若梯子与地面的夹角为a,则梯子顶端到地面的距离BC为( )
A. 3sina米 B. 3cosa米 C. 米 D. 米
第1题图 第2题图
2.(2018·金华)如图所示,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=a,∠ADC=β,则竹竿AB与AD的长度之比为( )
A. B. C. D.
3.(2019·威海)如图所示,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点,已知坡角为20°,山高BC=2千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
第3题图 第4题图
4.(2018·长春)如图所示,某地要修建高速公路,要从A地向B地修一条隧道(点A,B在同一
水平面上)为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为a,则A,B两地之间的距离为( )
800sina米 B. 800tana米 C. 米 D. 米
5.(2019·营口)如图所示,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
第5题图 第6题图
6.(2019·泰安)如图所示,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为________km( )
A.30+30 B.30+10 C.10+30 D.30
7.(2016·泰安)如图所示,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46?=0.7193,sin22?=0.3746,sin44?=0.6947)( )
A. 22.48 B. 41.68 C. 43.16 D. 55.63
第7题图 第8题图
8.(2015·泰安)如图所示,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50?方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A. 20海里 B. 40海里 C. 海里 D. 海里
9.(2014·泰安)如图1所示是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图2所示,再将图2沿DE折叠,使点A落在DC的延长线上的点A'处,如图3所示,则折痕DE的长为( )
A. cm B. 2 cm C. 2 cm D. 3 cm
10.(2012·泰安)如图所示,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( )
A. 3 B. 3.5 C. 2.5 D. 2.8
11.(2012·泰安)如图所示,为测量某物体AB的高度,在D点测得A点的仰角为30°朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A. 10米 B. 10米 C. 20米 D.米
12.(2018·广西)如图所示,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120 m,则乙楼的高CD是_________ m.(结果保留根号)
第12题图 第13题图
13.(2018·泰安)如图所示,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA′的延长线恰好过点C,则sin∠ABE的值为 _________。
14.(2013·泰安)如图所示,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为_______海里(取≈1.7,结果精确到0.1海里)
15.(2019·邵阳)某品牌太阳能热水器的实物图和横断面示意图如图所示.已知真空集热管DE与支架CB所在直线相交于点O,且OB=OE;支架BC与水平线AD垂直,AC=40 cm,∠ADE=30°,DE=190 cm,另一支架AB与水平线夹角∠BAD=65°,求OB的长度.(结果精确到1cm;温馨提示:sin65?≈0.91,cos65°≈0.42,tan65?≈2.14)
16.(2019·郴州)如图所示,巡逻船在A处测得灯塔C在北偏东45°方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东60°方向上,这时巡逻船与渔船的距离是多少?(精确到0.01 km.参考数据:≈1.414,≈1.732,≈2.449)
参考答案
知识构建
① ② ③ ④ ⑤1 ⑥ ⑦∠A+∠B=90°
⑧除直角外的两个条件,其中至少一个是边
考点训练
B 2.(1)< (2)< 3. C 4. 30° 5. 80° 6.
7,解:如图所示,过点C作CD⊥AB于点D.
∵∠A=60?,∠B=45?,∴∠ACD=30?。∠BCD=∠B=45?.
∴CD=AD?tanA,BD=CD.设AD=X,则CD=x·tan60?=x=8,
∵AB=AD+BD=x+x=8,∴x=4(-1).
∴CD=x=12-4.
∴S△ABC =AB·CD=×8×(12-4)=48-16.
8,解:如图所示,过点C作CD上AB于点D.
在Rt△ACD中,∠A=30?,AC=4.∴CD=2,AD=2.
∵AB=3,∴BD=.∴BC=。
9,解:设每层楼高为x米,
由题意得,MC'=MC-CC'=2. 5-1.5=1(米),
∴DC'=5x+1(米), EC'=4x+1(米).
在Rt△DC'A'中,∠DA'C'=60?,∴C'A'=米.
在Rt△EC'B'中,∠EB'C'=30°,∴C'B'==米。
∵A'B'=C'B'-C'A'=AB,∴-=14.解得x≈3.17.
∴5x+2.5≈18.4.
答:居民楼高约为18.4米.
10,解:(1)如图所示,过点F作FG⊥EC于点G。
由题意得,∠FDE=∠DEG=∠FGE=90°∴四边形DEGF是矩形,∴FG=DE.
在Rt△CDE中,DE=CE·tan∠DCE=2(米);∴点F到地面的距离为2米;
(2)∵坡度i=1:1.5,∴在Rt△CFG中,CG=1.5FG=3(米)∴FD=EG=3+6(米).
∵∠ADF=90°,∠AFD=45°,∴AD=DF=3+6(米).
在Rt△BCE中,BE=CE·tan∠BCE=6(米),
∴AB=AD+DE-BE=3+6+2-6=6-≈4.3(米)
答:宣传牌的高度约为4.3米.
11,解:如图所示,过点C作CD⊥AB于点D。
在Rt△BCD中,∵∠BDC=90°,sin33°=,∴BD=50×sin33?≈27.25(m)
∵cos33°=,∴CD=50×cos33°≈41.95(m).
∵∠ACD=45°,CD⊥AB,∴AD=CD=41.95(m)
∴AB=AD+BD=41.95+27.25=69.2(m)
答:A,B之间的距离约为69.2m.
真题训练
A 2. B 3. A 4. D 5. C 6. B 7. B 8. D 9. A 10. C 11. A 12. 40 13. 14. 67.5
15.解:设OE=OB=2x,∴OD=DE+OE=190+2x.
∵∠ADE=30°,∴OC=OD=95+x.∴BC=OC-OB=95+x-2x=95-x.
∵tan∠BAD=,∴2.14=,解得x=9.4.∴OB=2x≈19(cm).
答:OB的长度为19cm。
16.解:如图所示,延长CB交AD于点D,则∠CDA=90°。
在Rt△ADC中,AC=30(km),∠CAD=45?,∴AD=CD=AC=15(km)。
在Rt△ADB中,AD=15(km),∠BAD=30°,∴AB==10≈24.49(km)
答:巡逻船与渔船的距离约为24.49km
_21?????????è?????(www.21cnjy.com)_
