11.2.2 三角形的外角同步练习(含答案)
文档属性
| 名称 | 11.2.2 三角形的外角同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十一章 三角形11.2.2 三角形的外角
练习
一、单选题(共10小题)
1.(2019·河东区期中)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
2.(2019·成都市期末)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
A.80° B.70° C.85° D.75°
3.(2020·威海市期中)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
4.(2018·杭州市期中)如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
5.(2019·临沂市期中)一副三角板有两个直角三角形,如图叠放在一起,则的度数是( )
A.165° B.120° C.150° D.135°
6.(2019·启东市期中)已知,如图,AB∥CD,则图中α、β、γ三个角之间的数量关系为( )
A.α-β+γ=180° B.α+β-γ=180° C.α+β+γ=360° D.α-β-γ=90°
7.(2018·静安区期中)如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A.360° B.720° C.540° D.240°
8.(2018·沈阳市期中)如图,在△AEC中,点D和点F分别是AC和AE上的两点,连接DF,交CE的延长线于点B,若∠A=25°,∠B=45°,∠C=36°,则∠DFE=( )
A.103° B.104° C.105° D.106°
9.(2019·呼和浩特市期中)如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( )
A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5
10.(2018·海口市期中)如图,在Rt△ADB中,∠D=90°,C为AD上一点,则可能是( )
A.10° B.20° C.30° D.40°
二、填空题(共5小题)
11.(2018·伊春市期中)如图,D是△ABC的边AC上一点,E是BD上一点,连接EC,若∠A=60°,∠ABD=25°,∠DCE=35°,则∠BEC的度数为_____.
12.(2020·东莞市期末)如图,于点,,,则________.
13.(2019·浦东新区期中)如图,AB∥EF,若∠C=90°,那么x、y和z的关系是____________
14.(2019·南阳市期末)如图所示,_________.
15.(2019·防城港市期中)如图,在△ABC中,∠B=50°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_______°.
三、解答题(共2小题)
16.(2019·泉州市期末)在中,已知.
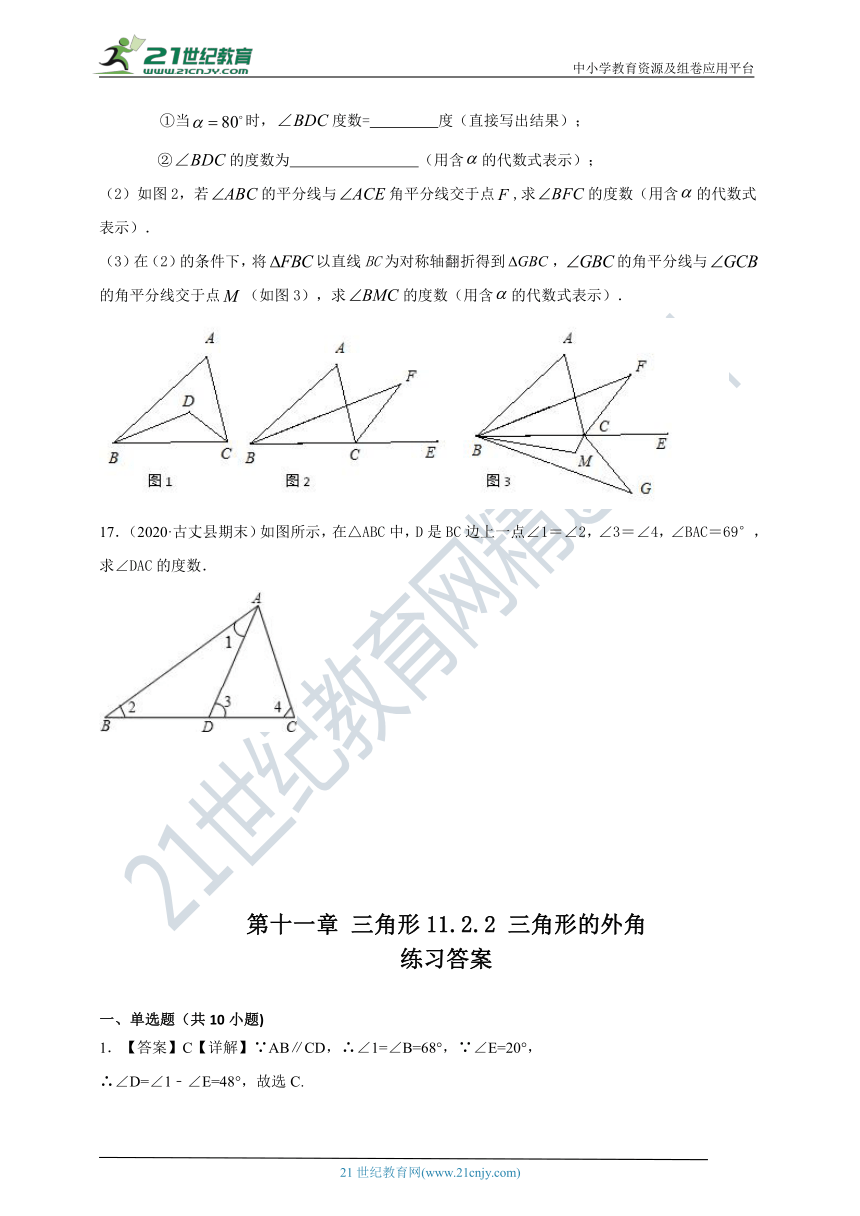
(1)如图1,的平分线相交于点.
①当时,度数= 度(直接写出结果);
②的度数为 (用含的代数式表示);
(2)如图2,若的平分线与角平分线交于点,求的度数(用含的代数式表示).
(3)在(2)的条件下,将以直线BC为对称轴翻折得到,的角平分线与的角平分线交于点(如图3),求的度数(用含的代数式表示).
17.(2020·古丈县期末)如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=69°,求∠DAC的度数.
第十一章 三角形11.2.2 三角形的外角
练习答案
一、单选题(共10小题)
1.【答案】C【详解】∵AB∥CD,∴∠1=∠B=68°,∵∠E=20°,
∴∠D=∠1﹣∠E=48°,故选C.
【答案】A【详解】如图,
∵∠1=∠3=55°,∠B=45°,∴∠4=∠3+∠B=100°,∵a∥b,∴∠5=∠4=100°,∴∠2=180°﹣∠5=80°,故选A.
3.【答案】C【详解】∵∠A=60°,∠B=40°,∴∠ACD=∠A+∠B=100°,∵CE平分∠ACD,
∴∠ECD=∠ACD=50°,故选C.
4.【答案】A【解析】
∵a∥b,∴∠1=∠4=35°,∵∠2=90°,∴∠4+∠5=90°,∴∠5=55°,∴∠3=180°-∠5=125°,故选:A.
5.
【答案】A【详解】∵图中是一副三角板,
∴∠1=45°,∴∠2=180°-∠1=180°-45°=135°,
∴ =∠2+30°=135°+30°=165°.故选A.
6.【答案】B【详解】如图,延长CD交AE于点F
∵AB∥CD∴β=∠AFD∵∠FDE+α=180°∴∠FDE=180°-α∵γ+∠FDE=∠ADF
∴γ+180°-α=β∴α+β-γ=180°故选B
7.【答案】D【解析】如图,
根据三角形的外角性质,∠1=∠A+∠C,∠2=∠B+∠D,
∵∠BOF=120°,∴∠3=180°﹣120°=60°,
根据三角形内角和定理,∠E+∠1=180°﹣60°=120°,
∠F+∠2=180°﹣60°=120°,所以,∠1+∠2+∠E+∠F=120°+120°=240°,
即∠A+∠B+∠C+∠D+∠E+∠F=240°.故选D.
8.【答案】D【详解】∵∠FEB是△AEC的一个外角,∠A=25°,∠C=36°,
∴∠FEB=∠A+∠C=61°,∵∠DFE是△BFE的一个外角,∠B=45°,
∴∠DFE=∠B+∠FEB=106°,故选D.
9.【答案】C【详解】解:设三个外角分别为2x,3x,4x,三角形外角和为360°,
所以2x+3x+4x=360°,所以x=40°,所以三个外角是80°,120°,160°,
所以对应内角比为5:3:1,故选C.
10.【答案】B【解析】根据三角形外角的性质可得:90°<6x<180°,解得:15°<x<30°.
二、填空题(共5小题)
11.【答案】120°【详解】
解:在△ABD中,∵∠A=60?,∠ABD=25?,∴∠CDE=∠A+∠ABD=60?+25?=85?,∴∠BEC=∠DCE+∠CDE=35?+85?=120?.故答案为:120?
12.【答案】20°【详解】根据题意,在△AED中,∠A=50°,∠D=20°,
∴∠BEO=∠A+∠D=70°,∵BC⊥ED于点O,
∴∠BOE=90°,∴∠B=90°-∠BEO=20°,故答案为20°.
13.【答案】x+y﹣z=90°.【详解】
过C作CM∥AB,延长CD交EF于N,
则∠CDE=∠E+∠CNE,即∠CNE=y﹣z∵CM∥AB,AB∥EF,
∴CM∥AB∥EF,∴∠ABC=x=∠1,∠2=∠CNE,
∵∠BCD=90°,∴∠1+∠2=90°,∴x+y﹣z=90°,
∴z+90°=y+x,即x+y﹣z=90°.故答案为x+y﹣z=90°.
14.
【答案】360°
【详解】如图延长交于点,
由三角形的外角等于与它不相邻的两个内角的和,得
,,
由等量代换,得,
.
故答案为:.
15.【答案】65【解析】
如图,∵AE平分∠DAC,CE平分∠ACF,
∴∠1=∠DAC,∠2=∠ACF,∴∠1+∠2=(∠DAC+∠ACF),
又∵∠DAC+∠ACF=(180°-∠BAC)+(180°-∠ACB)=360°-(∠BAC+∠ACB),且
∠BAC+∠ACB=180°-∠ABC=180°-50°=130°,
∴∠1+∠2=(360°-130°)=115°,
∴在△ACE中,∠E=180°-(∠1+∠2)=180°-115°=65°.
三、解答题(共2小题)
16【答案】(1)①;②;(2) (3)
【详解】(1)①;②;
(2)∵和分别平分和
∴,
∴
即
(3)由轴对称性质知:
由(1)②可得 ∴.
17.答案32°【详解】设∠1=∠2=x∴∠4=∠3=∠1+∠2=2x,在△ABC中,∠4+∠2+∠BAC=180°,
∴2x+x+69°=180°解得x=37.即∠1=∠2=37°,∠4=∠3=37°×2=74°.在△ADC中,∠4+∠3+∠DAC=180°
∴∠DAC=180?-∠4-∠3=180°-74°-74°=32?.
_21?????????è?????(www.21cnjy.com)_
第十一章 三角形11.2.2 三角形的外角
练习
一、单选题(共10小题)
1.(2019·河东区期中)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
2.(2019·成都市期末)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
A.80° B.70° C.85° D.75°
3.(2020·威海市期中)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
4.(2018·杭州市期中)如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
5.(2019·临沂市期中)一副三角板有两个直角三角形,如图叠放在一起,则的度数是( )
A.165° B.120° C.150° D.135°
6.(2019·启东市期中)已知,如图,AB∥CD,则图中α、β、γ三个角之间的数量关系为( )
A.α-β+γ=180° B.α+β-γ=180° C.α+β+γ=360° D.α-β-γ=90°
7.(2018·静安区期中)如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A.360° B.720° C.540° D.240°
8.(2018·沈阳市期中)如图,在△AEC中,点D和点F分别是AC和AE上的两点,连接DF,交CE的延长线于点B,若∠A=25°,∠B=45°,∠C=36°,则∠DFE=( )
A.103° B.104° C.105° D.106°
9.(2019·呼和浩特市期中)如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( )
A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5
10.(2018·海口市期中)如图,在Rt△ADB中,∠D=90°,C为AD上一点,则可能是( )
A.10° B.20° C.30° D.40°
二、填空题(共5小题)
11.(2018·伊春市期中)如图,D是△ABC的边AC上一点,E是BD上一点,连接EC,若∠A=60°,∠ABD=25°,∠DCE=35°,则∠BEC的度数为_____.
12.(2020·东莞市期末)如图,于点,,,则________.
13.(2019·浦东新区期中)如图,AB∥EF,若∠C=90°,那么x、y和z的关系是____________
14.(2019·南阳市期末)如图所示,_________.
15.(2019·防城港市期中)如图,在△ABC中,∠B=50°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_______°.
三、解答题(共2小题)
16.(2019·泉州市期末)在中,已知.
(1)如图1,的平分线相交于点.
①当时,度数= 度(直接写出结果);
②的度数为 (用含的代数式表示);
(2)如图2,若的平分线与角平分线交于点,求的度数(用含的代数式表示).
(3)在(2)的条件下,将以直线BC为对称轴翻折得到,的角平分线与的角平分线交于点(如图3),求的度数(用含的代数式表示).
17.(2020·古丈县期末)如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=69°,求∠DAC的度数.
第十一章 三角形11.2.2 三角形的外角
练习答案
一、单选题(共10小题)
1.【答案】C【详解】∵AB∥CD,∴∠1=∠B=68°,∵∠E=20°,
∴∠D=∠1﹣∠E=48°,故选C.
【答案】A【详解】如图,
∵∠1=∠3=55°,∠B=45°,∴∠4=∠3+∠B=100°,∵a∥b,∴∠5=∠4=100°,∴∠2=180°﹣∠5=80°,故选A.
3.【答案】C【详解】∵∠A=60°,∠B=40°,∴∠ACD=∠A+∠B=100°,∵CE平分∠ACD,
∴∠ECD=∠ACD=50°,故选C.
4.【答案】A【解析】
∵a∥b,∴∠1=∠4=35°,∵∠2=90°,∴∠4+∠5=90°,∴∠5=55°,∴∠3=180°-∠5=125°,故选:A.
5.
【答案】A【详解】∵图中是一副三角板,
∴∠1=45°,∴∠2=180°-∠1=180°-45°=135°,
∴ =∠2+30°=135°+30°=165°.故选A.
6.【答案】B【详解】如图,延长CD交AE于点F
∵AB∥CD∴β=∠AFD∵∠FDE+α=180°∴∠FDE=180°-α∵γ+∠FDE=∠ADF
∴γ+180°-α=β∴α+β-γ=180°故选B
7.【答案】D【解析】如图,
根据三角形的外角性质,∠1=∠A+∠C,∠2=∠B+∠D,
∵∠BOF=120°,∴∠3=180°﹣120°=60°,
根据三角形内角和定理,∠E+∠1=180°﹣60°=120°,
∠F+∠2=180°﹣60°=120°,所以,∠1+∠2+∠E+∠F=120°+120°=240°,
即∠A+∠B+∠C+∠D+∠E+∠F=240°.故选D.
8.【答案】D【详解】∵∠FEB是△AEC的一个外角,∠A=25°,∠C=36°,
∴∠FEB=∠A+∠C=61°,∵∠DFE是△BFE的一个外角,∠B=45°,
∴∠DFE=∠B+∠FEB=106°,故选D.
9.【答案】C【详解】解:设三个外角分别为2x,3x,4x,三角形外角和为360°,
所以2x+3x+4x=360°,所以x=40°,所以三个外角是80°,120°,160°,
所以对应内角比为5:3:1,故选C.
10.【答案】B【解析】根据三角形外角的性质可得:90°<6x<180°,解得:15°<x<30°.
二、填空题(共5小题)
11.【答案】120°【详解】
解:在△ABD中,∵∠A=60?,∠ABD=25?,∴∠CDE=∠A+∠ABD=60?+25?=85?,∴∠BEC=∠DCE+∠CDE=35?+85?=120?.故答案为:120?
12.【答案】20°【详解】根据题意,在△AED中,∠A=50°,∠D=20°,
∴∠BEO=∠A+∠D=70°,∵BC⊥ED于点O,
∴∠BOE=90°,∴∠B=90°-∠BEO=20°,故答案为20°.
13.【答案】x+y﹣z=90°.【详解】
过C作CM∥AB,延长CD交EF于N,
则∠CDE=∠E+∠CNE,即∠CNE=y﹣z∵CM∥AB,AB∥EF,
∴CM∥AB∥EF,∴∠ABC=x=∠1,∠2=∠CNE,
∵∠BCD=90°,∴∠1+∠2=90°,∴x+y﹣z=90°,
∴z+90°=y+x,即x+y﹣z=90°.故答案为x+y﹣z=90°.
14.
【答案】360°
【详解】如图延长交于点,
由三角形的外角等于与它不相邻的两个内角的和,得
,,
由等量代换,得,
.
故答案为:.
15.【答案】65【解析】
如图,∵AE平分∠DAC,CE平分∠ACF,
∴∠1=∠DAC,∠2=∠ACF,∴∠1+∠2=(∠DAC+∠ACF),
又∵∠DAC+∠ACF=(180°-∠BAC)+(180°-∠ACB)=360°-(∠BAC+∠ACB),且
∠BAC+∠ACB=180°-∠ABC=180°-50°=130°,
∴∠1+∠2=(360°-130°)=115°,
∴在△ACE中,∠E=180°-(∠1+∠2)=180°-115°=65°.
三、解答题(共2小题)
16【答案】(1)①;②;(2) (3)
【详解】(1)①;②;
(2)∵和分别平分和
∴,
∴
即
(3)由轴对称性质知:
由(1)②可得 ∴.
17.答案32°【详解】设∠1=∠2=x∴∠4=∠3=∠1+∠2=2x,在△ABC中,∠4+∠2+∠BAC=180°,
∴2x+x+69°=180°解得x=37.即∠1=∠2=37°,∠4=∠3=37°×2=74°.在△ADC中,∠4+∠3+∠DAC=180°
∴∠DAC=180?-∠4-∠3=180°-74°-74°=32?.
_21?????????è?????(www.21cnjy.com)_
