14.1.4 整式的乘法(3)课件(共19张PPT)
文档属性
| 名称 | 14.1.4 整式的乘法(3)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 16:40:55 | ||
图片预览






文档简介
(共19张PPT)
人教版
八年级数学上
14.1.4整式的乘法(3)
学习目标
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够运用多项式与多项式的乘法运算法则进行计算.(难点)
回顾旧知
2.计算:
1.说一说单项式乘以多项式的计算法则?
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
解:
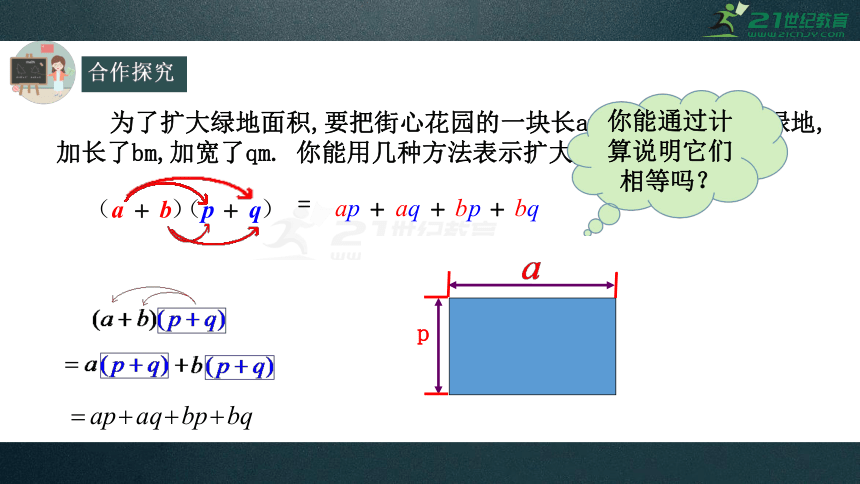
合作探究
为了扩大绿地面积,要把街心花园的一块长am,宽pm的长方形绿地,加长了bm,加宽了qm.
你能用几种方法表示扩大后的绿地面积?
你能通过计算说明它们相等吗?
b
q
q
b
p
p
=
合作探究
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
如何计算:
呢?
解:
你能得到多项式乘以多项式的方法吗?
多项式乘以多项式的法则:
=
典例精析
例1
计算:(1)(3x+1)(x+2);
(2)(x-8y)(x-y);
(3)
(x+y)(x2-xy+y2).
解:
(1)
原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
(2)
原式=x·x-xy-8xy+8y2
结果中有同类项
的要合并同类项.
=3x2+7x+2;
计算时要注意符号问题.
=x2-9xy+8y2;
典例精析
(3)
原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
=
x3+y3.
知识点拨:需要注意的几个问题:(1)漏乘;(2)符号问题;
(3)最后结果应化成最简形式.
计算时不能漏乘.
小试牛刀
1.计算:
小试牛刀
2、计算
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+_______.
x
(p+q)
pq
小试牛刀
3、
先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),
其中a=-1,b=1.
当a=-1,b=1时,
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
原式=-8+2-15=-21.
小试牛刀
4、若多项式(x2+mx+n)(x2-3x+4)展开后不含x3项和x2项,试求
m+2n的值.
解:(x2+mx+n)(x2-3x+4)
=x4
-3x3+4x2
+mx3-3mx2+4mx+
nx2
-3nx+4n
=x4+(m-3)x3+(n-3m+4)x2+(4m-3n)x+4n.
∵展开后不含x3和x2项,
∴所以m-3=0且n-3m+4=0,
解得m=3,n=5
∴m+2n=3+2×5=13.
课堂小结
今天我们收获了哪些知识?
1.说一说多项式与多项式相乘的运算法则?
2.在计算中应注意哪些问题?
综合演练
1.计算(x-2)(x-3)的结果为( )
A.x2+5x-6
B.x2-
5x-
6
C.x2+
5x+
6
D.x2-
5x+6
D
2.若(x+2)(x-1)=x2+mx+n,则m+n=(
)
A.1
B.-2
C.-1
D.2
C
综合演练
3.如图,长方形的长为a,宽为b,横、纵向阴影部分均为长方形,它们的宽都为c,则空白部分的面积是(
)
A.ab-bc+ac-c2
B.ab-bc-ac+c2
C.ab-ac-bc
D.ab-ac-bc-c2
B
综合演练
4.判别下列解法是否正确,若错,请说出理由.
解:原式
综合演练
解:原式
综合演练
5.化简求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.
解:原式=
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14
-56
=-20.
课后作业
教材105页习题14.1第5题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
14.1.4整式的乘法(3)
学习目标
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够运用多项式与多项式的乘法运算法则进行计算.(难点)
回顾旧知
2.计算:
1.说一说单项式乘以多项式的计算法则?
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
解:
合作探究
为了扩大绿地面积,要把街心花园的一块长am,宽pm的长方形绿地,加长了bm,加宽了qm.
你能用几种方法表示扩大后的绿地面积?
你能通过计算说明它们相等吗?
b
q
q
b
p
p
=
合作探究
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
如何计算:
呢?
解:
你能得到多项式乘以多项式的方法吗?
多项式乘以多项式的法则:
=
典例精析
例1
计算:(1)(3x+1)(x+2);
(2)(x-8y)(x-y);
(3)
(x+y)(x2-xy+y2).
解:
(1)
原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
(2)
原式=x·x-xy-8xy+8y2
结果中有同类项
的要合并同类项.
=3x2+7x+2;
计算时要注意符号问题.
=x2-9xy+8y2;
典例精析
(3)
原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
=
x3+y3.
知识点拨:需要注意的几个问题:(1)漏乘;(2)符号问题;
(3)最后结果应化成最简形式.
计算时不能漏乘.
小试牛刀
1.计算:
小试牛刀
2、计算
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+_______.
x
(p+q)
pq
小试牛刀
3、
先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),
其中a=-1,b=1.
当a=-1,b=1时,
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
原式=-8+2-15=-21.
小试牛刀
4、若多项式(x2+mx+n)(x2-3x+4)展开后不含x3项和x2项,试求
m+2n的值.
解:(x2+mx+n)(x2-3x+4)
=x4
-3x3+4x2
+mx3-3mx2+4mx+
nx2
-3nx+4n
=x4+(m-3)x3+(n-3m+4)x2+(4m-3n)x+4n.
∵展开后不含x3和x2项,
∴所以m-3=0且n-3m+4=0,
解得m=3,n=5
∴m+2n=3+2×5=13.
课堂小结
今天我们收获了哪些知识?
1.说一说多项式与多项式相乘的运算法则?
2.在计算中应注意哪些问题?
综合演练
1.计算(x-2)(x-3)的结果为( )
A.x2+5x-6
B.x2-
5x-
6
C.x2+
5x+
6
D.x2-
5x+6
D
2.若(x+2)(x-1)=x2+mx+n,则m+n=(
)
A.1
B.-2
C.-1
D.2
C
综合演练
3.如图,长方形的长为a,宽为b,横、纵向阴影部分均为长方形,它们的宽都为c,则空白部分的面积是(
)
A.ab-bc+ac-c2
B.ab-bc-ac+c2
C.ab-ac-bc
D.ab-ac-bc-c2
B
综合演练
4.判别下列解法是否正确,若错,请说出理由.
解:原式
综合演练
解:原式
综合演练
5.化简求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.
解:原式=
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14
-56
=-20.
课后作业
教材105页习题14.1第5题.
https://www.21cnjy.com/help/help_extract.php
