2020秋冀教版八年级数学上册16.1 轴对称课件(共41张PPT)
文档属性
| 名称 | 2020秋冀教版八年级数学上册16.1 轴对称课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 16:46:44 | ||
图片预览










文档简介
(共39张PPT)
第十六章 轴对称和中心对称
16.1 轴对称
1
轴对称图形
2
轴对称
3
轴对称的性质
4
轴对称的作图
CONTENTS
1
新知导入
看一看:观察下图中图形的构成,试着发现它们的规律.
CONTENTS
2
课程讲授
轴对称图形
问题1 如图,把一张纸对折,根据自己的喜好剪出图案(折痕处不要完全剪断),打开这张纸,得到一个美丽的窗花,多做几个这样的窗花,你能发现这些窗花有什么共同特点吗?
轴对称图形
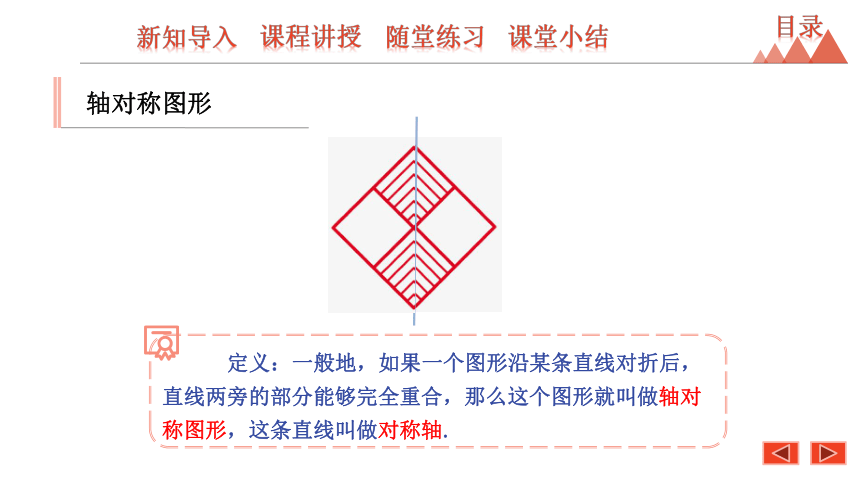
定义:一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.
轴对称图形
练一练:汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性.在下列四个汉字中,不是轴对称图形的是( )
D
轴对称图形
练一练:画出下列各图形的对称轴.
轴对称
问题1 下面每一对图形有什么共同特点?
每一对图形沿着虚线折叠,左边的图形能与右边的图形重合.
轴对称
A
B
C
A'
B'
C'
定义:一般地,如果两个图形沿某条直线对折后,这两个图形能完全重合,那么我们就说这两个图形成轴对称.这条直线叫做对称轴.
轴对称
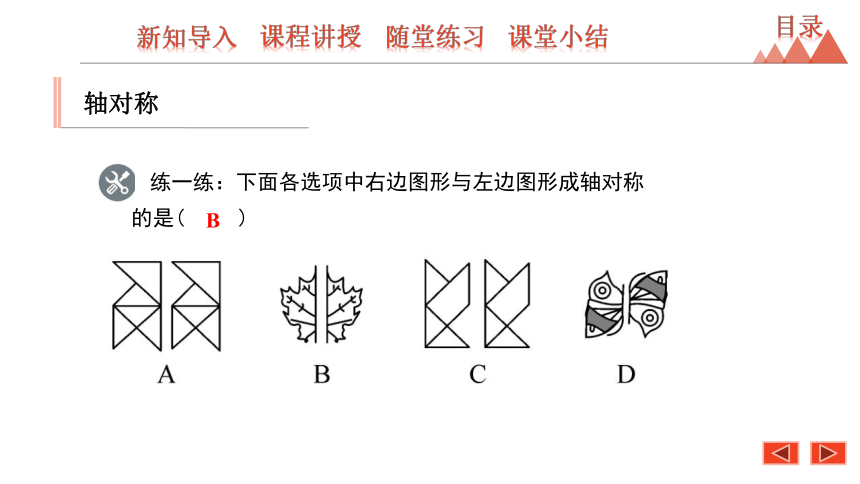
练一练:下面各选项中右边图形与左边图形成轴对称的是( )
B
轴对称
问题2.1 △ABC和△A'B'C'成轴对称,左边图形中的顶点、角、边与右
边图形的哪个顶点、角、边关于对称轴对称?
A'
B'
C'
A
B
C
A'
B'
C'
归纳: 关于对称轴对称的点、对称的线段、对称的角分别叫做对应点、对应线段、对应角.
轴对称
问题2.2 指出图中的对应点、对应线段和对应角.
A
B
C
A'
B'
C'
点A与点A',点B与点B',点C与点C'分别是对应点.线段AB与线段A'B',线段AC与线段A'C',线段BC与线段B'C'分别是对应线段.∠A与∠A',∠B与∠B',∠C与∠C'分别是对应角.
轴对称
问题3 你能结合具体的图形说明轴对称图形和两个图形成轴对称有
什么区别与联系吗?
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
轴对称的性质
问题1.1 成轴对称的两个图形全等吗?
全等
A
B
C
A'
B'
C'
A'
B'
C'
轴对称的性质
问题1.2 如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?
全等
轴对称的性质
问题2.1 如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点.
(1)线段AA′,BB′,CC′与直线MN有什么位置关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
轴对称的性质
(2)线段AB与A′B′,BC与B′C′有什么数量关系?
(3)∠A与∠A'有什么关系?∠B与∠B'呢?
AB =A′B′,BC=B′C′.
∠A=∠A',∠B=∠B'.
轴对称的性质
问题2.2 观察右图的轴对称图形,回答下列问题:
(1)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
B
C
D
D1
C1
B1
3
4
1
2
与对称轴垂直.
A
A1
轴对称的性质
(2)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
(3)∠1与∠2有什么关系 ∠3与∠4
呢?说说你的理由?
AD=A1D1,BC=B1C1.
∠1=∠2,∠3=∠4.
B
C
D
D1
C1
B1
3
4
1
2
A
A1
通过以上问题,你能得到什么结论?
轴对称的性质
归纳:如果两个图形关于某一条直线成轴对称,那么这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
成轴对称图形的性质对于轴对称图形同样适用.
轴对称的性质
A
B
C
A′
B′
C′
N
M
定义:垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
轴对称的性质
练一练:如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD
B.AF垂直平分EG
C.直线BG,CE的交点在AF上
D.△DEG是等边三角形
D
轴对称的作图
问题1 如果直线l外有线段AB,那么怎样画出线段AB关于直线l的对称线段A′B′?
l
A
B
A′
B′
轴对称的作图
问题2 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
提示:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
轴对称的作图
作法:(1)过点A画直线l的垂线,垂足为点
O,在垂线上截取OA′=OA,A′就是点A关于
直线l的对称点.
(2)同理,分别画出点B,C关于直线l的
对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
A
B
C
A′
B′
C′
O
试一试:画好后,用折叠的办法验证一下你的结果.
轴对称的作图
归纳: 几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的_______,连接这些对称点,就可以得到原图形的__________.
对称点
轴对称图形
轴对称的作图
例 如图,已知线段AB和直线l,画出线段AB关于直线l的对称线段.
●
A
B
●
轴对称的作图
如图 .
(1)分别过点A和点B画直线l的垂线
段AO和BO′,垂足分别为 O和O′ .
(2)分别延长AO到点A′,BO′到点B′,
使AO′= AO,B′O′=BO′.
(3)连接A′B′.线段A′B′即为所求.
●
A′
l
●
A
B
●
●
B′
解:
O
O'
轴对称的作图
做一做:如图是一个图案的一半,其中虚线是这个图案
的对称轴,画出这个图案的另一半.
CONTENTS
3
随堂练习
1.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B
2.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A.3
B.4
C.6
D.8
C
3.如图是一个轴对称图形的一半,请你以直线l为对称轴画出它的另一半.
4.如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)求AA1的长度.
A1
B1
C1
10
CONTENTS
4
课堂小结
轴对称
轴对称
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形
一般地,如果两个图形沿某条直线对折后,这两个图形能完全重合,那么我们就说这两个图形成轴对称
把成轴对称的两个图形看成一整体,它就是一个轴对称图形。把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称
联系
轴对称图形
轴对称
轴对称的作图
轴对称的性质
如果两个图形关于某一条直线成轴对称,那么这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
(1)找关键点;
(2)向对称轴作垂线;
(3)截取等长,确定对应点;
(4)依次连线,获得轴对称图形.
第十六章 轴对称和中心对称
16.1 轴对称
1
轴对称图形
2
轴对称
3
轴对称的性质
4
轴对称的作图
CONTENTS
1
新知导入
看一看:观察下图中图形的构成,试着发现它们的规律.
CONTENTS
2
课程讲授
轴对称图形
问题1 如图,把一张纸对折,根据自己的喜好剪出图案(折痕处不要完全剪断),打开这张纸,得到一个美丽的窗花,多做几个这样的窗花,你能发现这些窗花有什么共同特点吗?
轴对称图形
定义:一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.
轴对称图形
练一练:汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性.在下列四个汉字中,不是轴对称图形的是( )
D
轴对称图形
练一练:画出下列各图形的对称轴.
轴对称
问题1 下面每一对图形有什么共同特点?
每一对图形沿着虚线折叠,左边的图形能与右边的图形重合.
轴对称
A
B
C
A'
B'
C'
定义:一般地,如果两个图形沿某条直线对折后,这两个图形能完全重合,那么我们就说这两个图形成轴对称.这条直线叫做对称轴.
轴对称
练一练:下面各选项中右边图形与左边图形成轴对称的是( )
B
轴对称
问题2.1 △ABC和△A'B'C'成轴对称,左边图形中的顶点、角、边与右
边图形的哪个顶点、角、边关于对称轴对称?
A'
B'
C'
A
B
C
A'
B'
C'
归纳: 关于对称轴对称的点、对称的线段、对称的角分别叫做对应点、对应线段、对应角.
轴对称
问题2.2 指出图中的对应点、对应线段和对应角.
A
B
C
A'
B'
C'
点A与点A',点B与点B',点C与点C'分别是对应点.线段AB与线段A'B',线段AC与线段A'C',线段BC与线段B'C'分别是对应线段.∠A与∠A',∠B与∠B',∠C与∠C'分别是对应角.
轴对称
问题3 你能结合具体的图形说明轴对称图形和两个图形成轴对称有
什么区别与联系吗?
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
轴对称的性质
问题1.1 成轴对称的两个图形全等吗?
全等
A
B
C
A'
B'
C'
A'
B'
C'
轴对称的性质
问题1.2 如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?
全等
轴对称的性质
问题2.1 如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点.
(1)线段AA′,BB′,CC′与直线MN有什么位置关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
轴对称的性质
(2)线段AB与A′B′,BC与B′C′有什么数量关系?
(3)∠A与∠A'有什么关系?∠B与∠B'呢?
AB =A′B′,BC=B′C′.
∠A=∠A',∠B=∠B'.
轴对称的性质
问题2.2 观察右图的轴对称图形,回答下列问题:
(1)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
B
C
D
D1
C1
B1
3
4
1
2
与对称轴垂直.
A
A1
轴对称的性质
(2)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
(3)∠1与∠2有什么关系 ∠3与∠4
呢?说说你的理由?
AD=A1D1,BC=B1C1.
∠1=∠2,∠3=∠4.
B
C
D
D1
C1
B1
3
4
1
2
A
A1
通过以上问题,你能得到什么结论?
轴对称的性质
归纳:如果两个图形关于某一条直线成轴对称,那么这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
成轴对称图形的性质对于轴对称图形同样适用.
轴对称的性质
A
B
C
A′
B′
C′
N
M
定义:垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
轴对称的性质
练一练:如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD
B.AF垂直平分EG
C.直线BG,CE的交点在AF上
D.△DEG是等边三角形
D
轴对称的作图
问题1 如果直线l外有线段AB,那么怎样画出线段AB关于直线l的对称线段A′B′?
l
A
B
A′
B′
轴对称的作图
问题2 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
提示:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
轴对称的作图
作法:(1)过点A画直线l的垂线,垂足为点
O,在垂线上截取OA′=OA,A′就是点A关于
直线l的对称点.
(2)同理,分别画出点B,C关于直线l的
对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
A
B
C
A′
B′
C′
O
试一试:画好后,用折叠的办法验证一下你的结果.
轴对称的作图
归纳: 几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的_______,连接这些对称点,就可以得到原图形的__________.
对称点
轴对称图形
轴对称的作图
例 如图,已知线段AB和直线l,画出线段AB关于直线l的对称线段.
●
A
B
●
轴对称的作图
如图 .
(1)分别过点A和点B画直线l的垂线
段AO和BO′,垂足分别为 O和O′ .
(2)分别延长AO到点A′,BO′到点B′,
使AO′= AO,B′O′=BO′.
(3)连接A′B′.线段A′B′即为所求.
●
A′
l
●
A
B
●
●
B′
解:
O
O'
轴对称的作图
做一做:如图是一个图案的一半,其中虚线是这个图案
的对称轴,画出这个图案的另一半.
CONTENTS
3
随堂练习
1.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B
2.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A.3
B.4
C.6
D.8
C
3.如图是一个轴对称图形的一半,请你以直线l为对称轴画出它的另一半.
4.如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)求AA1的长度.
A1
B1
C1
10
CONTENTS
4
课堂小结
轴对称
轴对称
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形
一般地,如果两个图形沿某条直线对折后,这两个图形能完全重合,那么我们就说这两个图形成轴对称
把成轴对称的两个图形看成一整体,它就是一个轴对称图形。把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称
联系
轴对称图形
轴对称
轴对称的作图
轴对称的性质
如果两个图形关于某一条直线成轴对称,那么这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
(1)找关键点;
(2)向对称轴作垂线;
(3)截取等长,确定对应点;
(4)依次连线,获得轴对称图形.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
