2020秋冀教版八年级数学上册16.3 角的平分线课件(共29张PPT)
文档属性
| 名称 | 2020秋冀教版八年级数学上册16.3 角的平分线课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 16:58:22 | ||
图片预览








文档简介
(共29张PPT)
第十六章
轴对称和中心对称
16.3
角的平分线
1
角平分线的性质定理
2
角平分线性质定理的逆定理
3
尺规作角平分线
CONTENTS
1
新知导入
画一画:试着将下图中的角平分.
45°
30°
15°
22.5°
想一想:除了使用量角器,你还有其他更为准确的方法吗?
CONTENTS
2
课程讲授
角平分线的性质定理
问题1
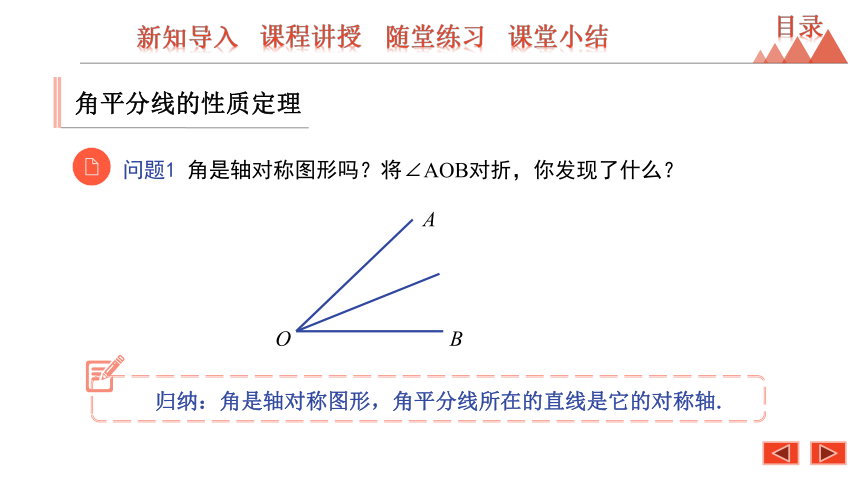
角是轴对称图形吗?将∠AOB对折,你发现了什么?
A
B
O
归纳:角是轴对称图形,角平分线所在的直线是它的对称轴.
角平分线的性质定理
问题1.1
如图,在∠AOB中,OC平分∠AOB.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D、E,测量PD,PE并作比较,你得到什么结论?
A
O
B
C
P
D
E
PD=PE
角平分线的性质定理
问题1.2
在OC上多取几个点进行测量和比较,得到的结论一致吗?试着猜想角的平分线的性质.
A
O
B
C
P
D
E
P'
D'
E'
PD'=PE'
猜想:角的平分线上的点到角的两边的距离相等.
角平分线的性质定理
问题2
运用所学知识证明你的猜想.
已知:如图,
OC是
∠AOB的平分线,P是OC上任意一点,PD⊥OA,
PE⊥OB,垂足分别为D,E.
求证:PD=PE.
A
O
B
C
P
D
E
角平分线的性质定理
证明:在△PDO和△PEO中,
∠1=
∠2,
∠PDO=
∠PEO=90°,
OP=
OP,
∴
△PDO
≌△PEO(AAS).
∴PD=PE.
A
O
B
C
P
D
E
1
2
角平分线的性质定理
归纳:
角平分线的性质定理:
角_________的点到这个角的两边的距离_____.
角平分线的性质定理(几何语言):
∵OP
是∠AOB的平分线,
PD⊥____,PE⊥____,
∴PD
=
____.
平分线上
相等
OA
OB
PE
B
A
D
O
P
E
C
角平分线的性质定理
练一练:如图,OP平分∠AOB,PC⊥OA,垂足为C,PD⊥OB,垂足为D,则PC与PD的大小关系是(
)
A.PC>PD
B.PC=PD
C.PCD.不能确定
B
角平分线的性质定理
练一练:如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D,E,PD=6cm,则PE=______cm.
B
A
C
P
M
D
E
6
角平分线性质定理的逆定理
问题1.1
写出角平分线的性质定理的逆命题.
如果角内部一点到角两边的距离相等,那么这个点在这个角的角平分线上
问题1.2
这个逆命题是否正确?
猜想:这个逆命题正确
问题1.3
设法验证你的猜想.
角平分线性质定理的逆定理
归纳:
角平分线性质定理的逆定理:
到角的两边
的点在角平分线上.
距离相等
角平分线性质定理的逆定理
例
已知:如图,△ABC的两内角∠B,∠C
的角平分线相交于点P.
求证:点P在∠A的角平分线上.
P
A
B
C
D
F
E
证明:分别过点P做PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F.
∵
∠B,∠C
的角平分线相交于点P,
∴PD=PF,PE=PF,
∴
PD=PE,
∴点P在∠A的角平分线上.
角平分线性质定理的逆定理
归纳:三角形的平分线:
三角形的三条角平分线_________,并且这点到三边的距离______.
即PD=____=_____.
交于一点
相等
A
B
C
P
N
M
D
E
F
PE
PF
尺规作角平分线
问题1
如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
D
E
C
两个三角形三边对应相等,两个三角形全等,两全等三角形的对应角相等.所以AE就是角平分线
想一想:能够运用这种方法作出任意角的角平分
线吗?
尺规作角平分线
问题2
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,
分别交OA,OB于点D,E.
(2)分别以点D,E为圆心,适当长为半
径,在∠AOB内部画弧,两弧相交于点C.
(3)作射线OC.射线OC即为所求.
A
O
B
E
D
C
尺规作角平分线
练一练:用直尺和圆规作一个角的平分线的示意图如图所示,则
能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
CONTENTS
3
随堂练习
1.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于
EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠CDA的度数为________.
65°
2.如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4.则点P到AB的距离为_______.
A
B
C
P
4
3.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=________.
35°
4.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6
B.5
C.4
D.3
B
A
C
D
E
D
5.求证:有两个角及其中一个角的角平分线对应相等的两个三角形全等.
已知:如图,在△ABC和△A′B′C′中,∠B=∠B′,
∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的平分线,且AD=A′D′.
求证:△ABC≌△A′B′C′.
A
B
C
D
A'
B'
C'
D'
证明:∵∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的角平分线,∴∠BAD=∠B′A′D′.
又∵∠B=∠B′,AD=A′D′,
∴△ABD≌△A′B′D′(AAS),∴AB=A′B′,
在△ABC和△A′B′C′中,
∠B=∠B′,
AB=A′B′,
∠BAC=∠B′A′C′,
∴△ABC≌△A′B′C′(ASA).
A
B
C
D
A'
B'
C'
D'
CONTENTS
4
课堂小结
角的平分线
角平分线的性质定理
角平分线上的点到角两边的距离相等
尺规作角平分线
角平分线性质定理的逆定理
到角的两边距离相等的点在角平分线上.
第十六章
轴对称和中心对称
16.3
角的平分线
1
角平分线的性质定理
2
角平分线性质定理的逆定理
3
尺规作角平分线
CONTENTS
1
新知导入
画一画:试着将下图中的角平分.
45°
30°
15°
22.5°
想一想:除了使用量角器,你还有其他更为准确的方法吗?
CONTENTS
2
课程讲授
角平分线的性质定理
问题1
角是轴对称图形吗?将∠AOB对折,你发现了什么?
A
B
O
归纳:角是轴对称图形,角平分线所在的直线是它的对称轴.
角平分线的性质定理
问题1.1
如图,在∠AOB中,OC平分∠AOB.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D、E,测量PD,PE并作比较,你得到什么结论?
A
O
B
C
P
D
E
PD=PE
角平分线的性质定理
问题1.2
在OC上多取几个点进行测量和比较,得到的结论一致吗?试着猜想角的平分线的性质.
A
O
B
C
P
D
E
P'
D'
E'
PD'=PE'
猜想:角的平分线上的点到角的两边的距离相等.
角平分线的性质定理
问题2
运用所学知识证明你的猜想.
已知:如图,
OC是
∠AOB的平分线,P是OC上任意一点,PD⊥OA,
PE⊥OB,垂足分别为D,E.
求证:PD=PE.
A
O
B
C
P
D
E
角平分线的性质定理
证明:在△PDO和△PEO中,
∠1=
∠2,
∠PDO=
∠PEO=90°,
OP=
OP,
∴
△PDO
≌△PEO(AAS).
∴PD=PE.
A
O
B
C
P
D
E
1
2
角平分线的性质定理
归纳:
角平分线的性质定理:
角_________的点到这个角的两边的距离_____.
角平分线的性质定理(几何语言):
∵OP
是∠AOB的平分线,
PD⊥____,PE⊥____,
∴PD
=
____.
平分线上
相等
OA
OB
PE
B
A
D
O
P
E
C
角平分线的性质定理
练一练:如图,OP平分∠AOB,PC⊥OA,垂足为C,PD⊥OB,垂足为D,则PC与PD的大小关系是(
)
A.PC>PD
B.PC=PD
C.PC
B
角平分线的性质定理
练一练:如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D,E,PD=6cm,则PE=______cm.
B
A
C
P
M
D
E
6
角平分线性质定理的逆定理
问题1.1
写出角平分线的性质定理的逆命题.
如果角内部一点到角两边的距离相等,那么这个点在这个角的角平分线上
问题1.2
这个逆命题是否正确?
猜想:这个逆命题正确
问题1.3
设法验证你的猜想.
角平分线性质定理的逆定理
归纳:
角平分线性质定理的逆定理:
到角的两边
的点在角平分线上.
距离相等
角平分线性质定理的逆定理
例
已知:如图,△ABC的两内角∠B,∠C
的角平分线相交于点P.
求证:点P在∠A的角平分线上.
P
A
B
C
D
F
E
证明:分别过点P做PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F.
∵
∠B,∠C
的角平分线相交于点P,
∴PD=PF,PE=PF,
∴
PD=PE,
∴点P在∠A的角平分线上.
角平分线性质定理的逆定理
归纳:三角形的平分线:
三角形的三条角平分线_________,并且这点到三边的距离______.
即PD=____=_____.
交于一点
相等
A
B
C
P
N
M
D
E
F
PE
PF
尺规作角平分线
问题1
如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
D
E
C
两个三角形三边对应相等,两个三角形全等,两全等三角形的对应角相等.所以AE就是角平分线
想一想:能够运用这种方法作出任意角的角平分
线吗?
尺规作角平分线
问题2
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,
分别交OA,OB于点D,E.
(2)分别以点D,E为圆心,适当长为半
径,在∠AOB内部画弧,两弧相交于点C.
(3)作射线OC.射线OC即为所求.
A
O
B
E
D
C
尺规作角平分线
练一练:用直尺和圆规作一个角的平分线的示意图如图所示,则
能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
CONTENTS
3
随堂练习
1.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于
EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠CDA的度数为________.
65°
2.如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4.则点P到AB的距离为_______.
A
B
C
P
4
3.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=________.
35°
4.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6
B.5
C.4
D.3
B
A
C
D
E
D
5.求证:有两个角及其中一个角的角平分线对应相等的两个三角形全等.
已知:如图,在△ABC和△A′B′C′中,∠B=∠B′,
∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的平分线,且AD=A′D′.
求证:△ABC≌△A′B′C′.
A
B
C
D
A'
B'
C'
D'
证明:∵∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的角平分线,∴∠BAD=∠B′A′D′.
又∵∠B=∠B′,AD=A′D′,
∴△ABD≌△A′B′D′(AAS),∴AB=A′B′,
在△ABC和△A′B′C′中,
∠B=∠B′,
AB=A′B′,
∠BAC=∠B′A′C′,
∴△ABC≌△A′B′C′(ASA).
A
B
C
D
A'
B'
C'
D'
CONTENTS
4
课堂小结
角的平分线
角平分线的性质定理
角平分线上的点到角两边的距离相等
尺规作角平分线
角平分线性质定理的逆定理
到角的两边距离相等的点在角平分线上.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
