2020秋冀教版八年级数学上册17.2 直角三角形课件(共32张PPT)
文档属性
| 名称 | 2020秋冀教版八年级数学上册17.2 直角三角形课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 00:00:00 | ||
图片预览






文档简介
(共32张PPT)
第十七章
特殊三角形
17.2
直角三角形
1
直角三角形的性质与判定
2
直角三角形斜边上的中线性质
3
含30°角的直角三角形的性质
CONTENTS
1
新知导入
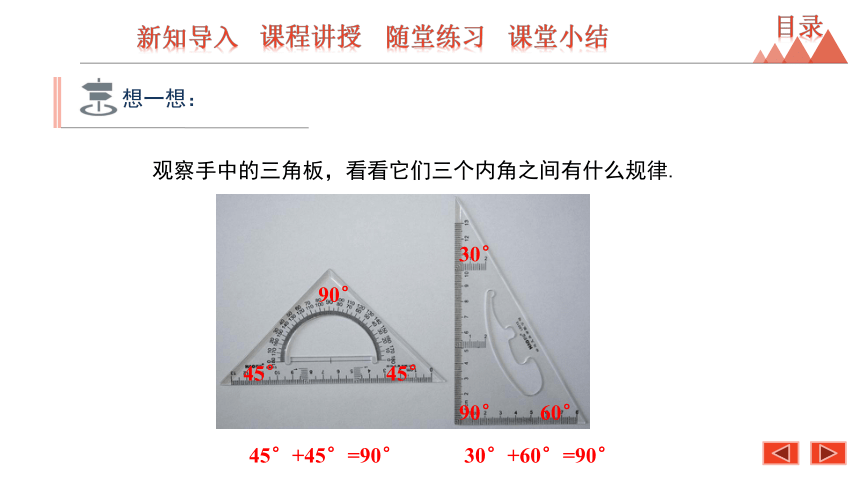
想一想:
观察手中的三角板,看看它们三个内角之间有什么规律.
45°+45°=90°
45°
45°
90°
30°+60°=90°
30°
60°
90°
CONTENTS
2
课程讲授
直角三角形的性质与判定
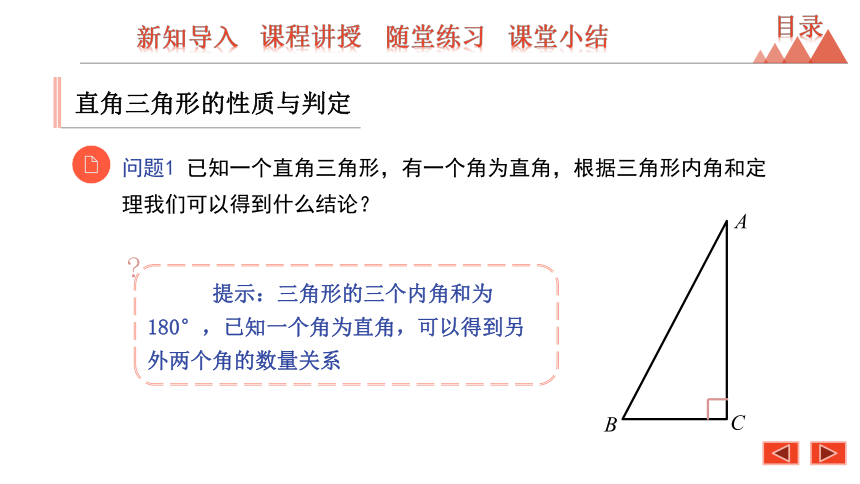
问题1
已知一个直角三角形,有一个角为直角,根据三角形内角和定理我们可以得到什么结论?
A
B
C
提示:三角形的三个内角和为180°,已知一个角为直角,可以得到另外两个角的数量关系
?
直角三角形的性质与判定
A
B
C
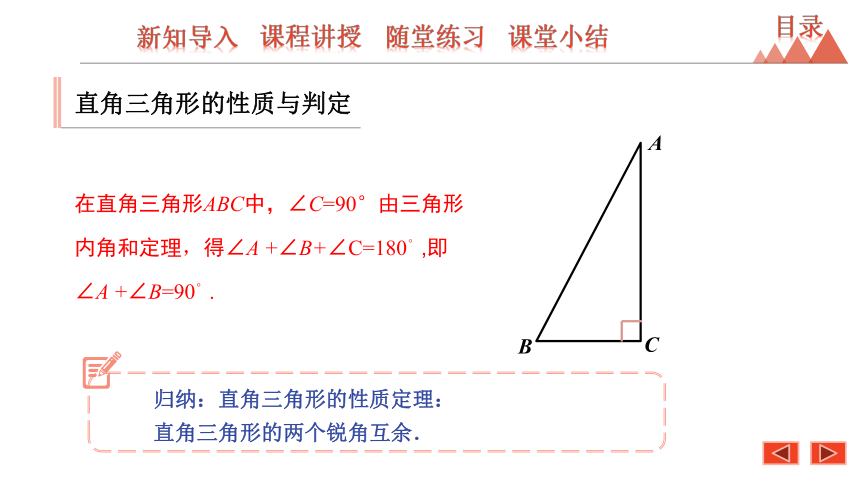
在直角三角形ABC中,∠C=90°由三角形内角和定理,得∠A
+∠B+∠C=180°,即
∠A
+∠B=90°.
归纳:直角三角形的性质定理:
直角三角形的两个锐角互余.
直角三角形的性质与判定
归纳:
直角三角形性质的应用格式:
在直角三角形ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=____.
直角三角形的表示方法:
直角三角形可以用符号“______”表示,直角三角形
ABC
可以写成___
____
.
90°
Rt△
Rt△ABC
直角三角形的性质与判定
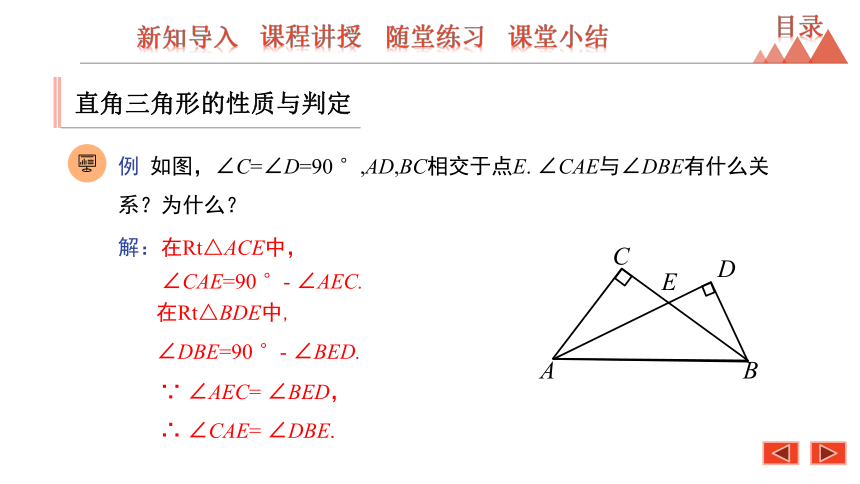
例
如图,∠C=∠D=90
°,AD,BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△ACE中,
∠CAE=90
°-
∠AEC.
在Rt△BDE中,
∠DBE=90
°-
∠BED.
∵
∠AEC=
∠BED,
∴
∠CAE=
∠DBE.
直角三角形的性质与判定
练一练:如图是一张长方形纸片,剪去部分后得到一个三角形,
则图中∠1+∠2的度数是(
)
A.30°
B.60°
C.90°
D.120°
1
2
C
直角三角形的性质与判定
问题2.1
我们已经知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?
1
2
∠1+∠2=90°
提示:三角形的三个内角和为180°,已知两个角的数量关系,可以得到另外一个角的大小.
?
直角三角形的性质与判定
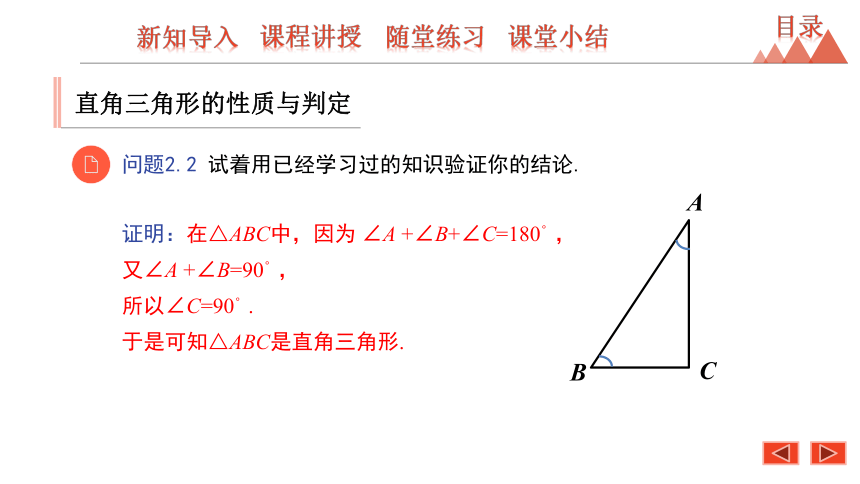
问题2.2
试着用已经学习过的知识验证你的结论.
证明:在△ABC中,因为
∠A
+∠B+∠C=180°,
又∠A
+∠B=90°,
所以∠C=90°.
于是可知△ABC是直角三角形.
A
B
C
直角三角形的性质与判定
归纳:
直角三角形的判定定理:
如果一个三角形的两个角_____,那么这个三角形是直
角三角形.
直角三角形判定定理的应用格式:
在三角形ABC
中,
∵∠A
+∠B
=____,
∴三角形ABC
是___________.
互余
90°
直角三角形
直角三角形的性质与判定
练一练:(1)如图,图中直角三角形共有(
)
A.1个
B.2个
C.3个
D.4个
(2)如图,∠C=90
°,
∠1=
∠2,△ADE是______三角形.
C
直角
A
C
B
D
E
(
(
1
2
直角三角形斜边上的中线性质
问题1
在一张半透明的纸上画出Rt△ABC,∠C=90°,如图(1);
B
A
C
E
F
(B)
将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE,
如图(2);
将纸展开,如图(3)
.
B
A
C
(1)
(2)
B
A
C
E
F
(3)
直角三角形斜边上的中线性质
问题1
(1)∠ECF与∠B有怎样的关系?线段EC与线段EB有怎样的关系?
∠ECF=∠B
EC=EB
(2)由发现的上述关系以及∠A+∠B=∠ACB,∠ACE+∠ECF=∠ACB,你能判断∠ACE与∠A的大小关系吗?线段AE与线段CE呢?
∠ACE=∠A
AE=CE
(3)由发现的上述关系,你能猜想线段CE与线段AB的关系吗?
猜想:CE=AE=EB,即CE是AB的中线,且CE=
AB.
直角三角形斜边上的中线性质
问题2
试着运用所学知识,验证你的猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD
是斜边AB上的中线.
求证:CD=
AB.
B
A
C
D
直角三角形斜边上的中线性质
证明:如图,过点D,作DE∥BC,交AC于点E;
作DF∥AC,交BC于点F.
在△AED
和△DFB
中,
∠A=∠FDB(两直线平行,同位角相等),
∵
AD=DB(中线的概念),
∠ADE=∠B(两直线平行,同位角相等),
∴△AED≌△DFB
(ASA).
∴QE=DF,ED=FB.
(全等三角形的对应边相等)
F
E
B
A
C
D
直角三角形斜边上的中线性质
F
E
B
A
C
D
同理可证,△CDE≌△DCF.
从而,ED=FC,EC=FD.
∴
AE=EC,CF=FB.(等量代换)
又∵DE⊥AC,DF⊥BC,(两直线平行,同位角相等)
∴DE为AC的垂直平分线,
DF为BC的垂直平分线.
∴AD=CD=BD(线段垂直平分线的性质定理).
CD=
AB.
直角三角形斜边上的中线性质
归纳:直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
直角三角形斜边上的中线性质
练一练:如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M、C两点间的距离为(
)
A.0.5km
B.0.6km
C.0.9km
D.1.2km
D
含30°角的直角三角形的性质
例
Rt△ABC中,∠ACB=90
°
,∠A=30°,
求证:BC=
AB.
B
A
C
证明:
作斜边上的中线CD,
D
则CD=AD=BD=
AB
∵
∠A=30°,
∴
∠B=60°
∴
△CDB是等边三角形,
∴
BC=BD=
AB
含30°角的直角三角形的性质
归纳:含30°角的直角三角形的性质:
在直角三角形中,30°角所对的直角边等于斜边的一半.
含30°角的直角三角形的性质
练一练:
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=________.
2
CONTENTS
3
随堂练习
1.如图,E是△ABC中AC边上的一点,过E作ED⊥AB,垂足
为D.若∠1=∠2,则△ABC是______三角形.
直角
2.具备下列条件的△ABC中,不是直角三角形的是
(
)
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
3.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=26°,则∠BDC的度数是(
)
A.26°
B.38°
C.42°
D.52°
D
4.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为(
)
A.20
B.18
C.14
D.13
C
5.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=4
cm,则AB等于(
)
A.9
cm
B.8
cm
C.7
cm
D.6
cm
B
6.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
CONTENTS
4
课堂小结
直角三角形
性质定理
直角三角形的两个锐角互余
判定定理
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半
在直角三角形中,30°角所对的直角边等于斜边的一半
第十七章
特殊三角形
17.2
直角三角形
1
直角三角形的性质与判定
2
直角三角形斜边上的中线性质
3
含30°角的直角三角形的性质
CONTENTS
1
新知导入
想一想:
观察手中的三角板,看看它们三个内角之间有什么规律.
45°+45°=90°
45°
45°
90°
30°+60°=90°
30°
60°
90°
CONTENTS
2
课程讲授
直角三角形的性质与判定
问题1
已知一个直角三角形,有一个角为直角,根据三角形内角和定理我们可以得到什么结论?
A
B
C
提示:三角形的三个内角和为180°,已知一个角为直角,可以得到另外两个角的数量关系
?
直角三角形的性质与判定
A
B
C
在直角三角形ABC中,∠C=90°由三角形内角和定理,得∠A
+∠B+∠C=180°,即
∠A
+∠B=90°.
归纳:直角三角形的性质定理:
直角三角形的两个锐角互余.
直角三角形的性质与判定
归纳:
直角三角形性质的应用格式:
在直角三角形ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=____.
直角三角形的表示方法:
直角三角形可以用符号“______”表示,直角三角形
ABC
可以写成___
____
.
90°
Rt△
Rt△ABC
直角三角形的性质与判定
例
如图,∠C=∠D=90
°,AD,BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△ACE中,
∠CAE=90
°-
∠AEC.
在Rt△BDE中,
∠DBE=90
°-
∠BED.
∵
∠AEC=
∠BED,
∴
∠CAE=
∠DBE.
直角三角形的性质与判定
练一练:如图是一张长方形纸片,剪去部分后得到一个三角形,
则图中∠1+∠2的度数是(
)
A.30°
B.60°
C.90°
D.120°
1
2
C
直角三角形的性质与判定
问题2.1
我们已经知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?
1
2
∠1+∠2=90°
提示:三角形的三个内角和为180°,已知两个角的数量关系,可以得到另外一个角的大小.
?
直角三角形的性质与判定
问题2.2
试着用已经学习过的知识验证你的结论.
证明:在△ABC中,因为
∠A
+∠B+∠C=180°,
又∠A
+∠B=90°,
所以∠C=90°.
于是可知△ABC是直角三角形.
A
B
C
直角三角形的性质与判定
归纳:
直角三角形的判定定理:
如果一个三角形的两个角_____,那么这个三角形是直
角三角形.
直角三角形判定定理的应用格式:
在三角形ABC
中,
∵∠A
+∠B
=____,
∴三角形ABC
是___________.
互余
90°
直角三角形
直角三角形的性质与判定
练一练:(1)如图,图中直角三角形共有(
)
A.1个
B.2个
C.3个
D.4个
(2)如图,∠C=90
°,
∠1=
∠2,△ADE是______三角形.
C
直角
A
C
B
D
E
(
(
1
2
直角三角形斜边上的中线性质
问题1
在一张半透明的纸上画出Rt△ABC,∠C=90°,如图(1);
B
A
C
E
F
(B)
将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE,
如图(2);
将纸展开,如图(3)
.
B
A
C
(1)
(2)
B
A
C
E
F
(3)
直角三角形斜边上的中线性质
问题1
(1)∠ECF与∠B有怎样的关系?线段EC与线段EB有怎样的关系?
∠ECF=∠B
EC=EB
(2)由发现的上述关系以及∠A+∠B=∠ACB,∠ACE+∠ECF=∠ACB,你能判断∠ACE与∠A的大小关系吗?线段AE与线段CE呢?
∠ACE=∠A
AE=CE
(3)由发现的上述关系,你能猜想线段CE与线段AB的关系吗?
猜想:CE=AE=EB,即CE是AB的中线,且CE=
AB.
直角三角形斜边上的中线性质
问题2
试着运用所学知识,验证你的猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD
是斜边AB上的中线.
求证:CD=
AB.
B
A
C
D
直角三角形斜边上的中线性质
证明:如图,过点D,作DE∥BC,交AC于点E;
作DF∥AC,交BC于点F.
在△AED
和△DFB
中,
∠A=∠FDB(两直线平行,同位角相等),
∵
AD=DB(中线的概念),
∠ADE=∠B(两直线平行,同位角相等),
∴△AED≌△DFB
(ASA).
∴QE=DF,ED=FB.
(全等三角形的对应边相等)
F
E
B
A
C
D
直角三角形斜边上的中线性质
F
E
B
A
C
D
同理可证,△CDE≌△DCF.
从而,ED=FC,EC=FD.
∴
AE=EC,CF=FB.(等量代换)
又∵DE⊥AC,DF⊥BC,(两直线平行,同位角相等)
∴DE为AC的垂直平分线,
DF为BC的垂直平分线.
∴AD=CD=BD(线段垂直平分线的性质定理).
CD=
AB.
直角三角形斜边上的中线性质
归纳:直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
直角三角形斜边上的中线性质
练一练:如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M、C两点间的距离为(
)
A.0.5km
B.0.6km
C.0.9km
D.1.2km
D
含30°角的直角三角形的性质
例
Rt△ABC中,∠ACB=90
°
,∠A=30°,
求证:BC=
AB.
B
A
C
证明:
作斜边上的中线CD,
D
则CD=AD=BD=
AB
∵
∠A=30°,
∴
∠B=60°
∴
△CDB是等边三角形,
∴
BC=BD=
AB
含30°角的直角三角形的性质
归纳:含30°角的直角三角形的性质:
在直角三角形中,30°角所对的直角边等于斜边的一半.
含30°角的直角三角形的性质
练一练:
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=________.
2
CONTENTS
3
随堂练习
1.如图,E是△ABC中AC边上的一点,过E作ED⊥AB,垂足
为D.若∠1=∠2,则△ABC是______三角形.
直角
2.具备下列条件的△ABC中,不是直角三角形的是
(
)
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
3.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=26°,则∠BDC的度数是(
)
A.26°
B.38°
C.42°
D.52°
D
4.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为(
)
A.20
B.18
C.14
D.13
C
5.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=4
cm,则AB等于(
)
A.9
cm
B.8
cm
C.7
cm
D.6
cm
B
6.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
CONTENTS
4
课堂小结
直角三角形
性质定理
直角三角形的两个锐角互余
判定定理
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半
在直角三角形中,30°角所对的直角边等于斜边的一半
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
