人教版 九年级数学上册 22.1 二次函数的图象及其性质 同步测试(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 22.1 二次函数的图象及其性质 同步测试(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 137.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 00:00:00 | ||
图片预览



文档简介
2020-2021学年人教版
九年级数学上册
22.1
二次函数的图象及其性质
同步测试(含答案)
1.
已知抛物线c:y=x2+2x-3,将抛物线c平移得到抛物线c',如果两条抛物线关于直线x=1对称,那么下列说法正确的是
( )
A.将抛物线c沿x轴向右平移个单位得到抛物线c'
B.将抛物线c沿x轴向右平移4个单位得到抛物线c'
C.将抛物线c沿x轴向右平移个单位得到抛物线c'
D.将抛物线c沿x轴向右平移6个单位得到抛物线c'
2.已知二次函数y=x2-x+m-1的图象与x轴有交点,则m的取值范围是
( )
A.m≤5
B.m≥2
C.m<5
D.m>2
3.
抛物线y=-x2+4x-4与坐标轴的交点个数为
( )
A.0
B.1
C.2
D.3
4.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为直线x=-1,则使函数值y>0成立的x的取值范围是
( )
A.x<-4或x>2
B.-4≤x≤2
C.x≤-4或x≥2
D.-45.将二次函数y=x2-4x+a的图象向左平移一个单位,再向上平移一个单位,若得到的函数图象与直线y=2有两个交点,则a的取值范围是
( )
A.a>3
B.a<3
C.a>5
D.a<5
6.已知二次函数y=(x-a-1)(x-a+1)-3a+7(其中x是自变量)的图象与x轴没有公共点,且当x<-1时,y随x的增大而减小,则实数a的取值范围是
( )
A.a<2
B.a>-1
C.-1D.-1≤a<2
7.已知m>0,关于x的一元二次方程(x+1)(x-2)-m=0的解为x1,x2(x1( )
A.x1<-1<2B.-1C.-1D.x1<-18.在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则
( )
A.M=N-1或M=N+1
B.M=N-1或M=N+2
C.M=N或M=N+1
D.M=N或M=N-1
9.将抛物线y=3(x+1)2-2向上平移1个单位,再向左平移1个单位得到的抛物线的解析式是 .?
10.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则方程ax2=bx+c的解是 .?
11.已知二次函数y=x2-4x+k的图象的顶点在x轴下方,则实数k的取值范围是 .?
12.已知函数y=的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为 .?
13.在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下:
x
…
-1
0
1
2
3
…
y甲
…
6
3
2
3
6
…
乙写错了常数项,列表如下:
x
…
-1
0
1
2
3
…
y乙
…
-2
-1
2
7
14
…
通过上述信息,解决以下问题:
(1)求原二次函数y=ax2+bx+c(a≠0)的表达式;
(2)对于二次函数y=ax2+bx+c(a≠0),当x 时,y的值随x的值增大而增大;?
(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,求k的取值范围.
14.
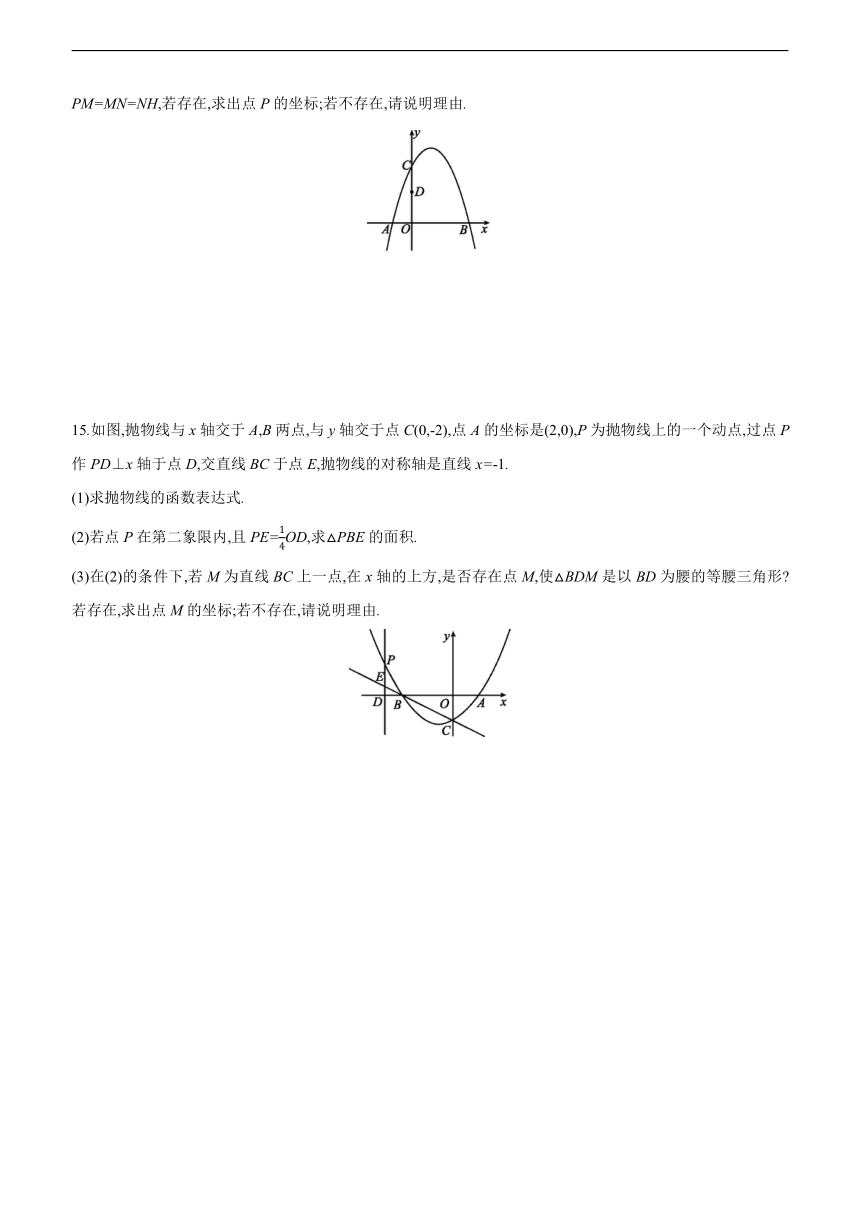
如图,二次函数y=-x2+bx+3的图象与x轴交于点A,B,与y轴交于点C,点A的坐标为(-1,0),点D为OC的中点,点P在抛物线上.
(1)b= .?
(2)若点P在第一象限,过点P作PH⊥x轴,垂足为H,PH与BC,BD分别交于点M,N.是否存在这样的点P,使得PM=MN=NH,若存在,求出点P的坐标;若不存在,请说明理由.
15.如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,-2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.
(1)求抛物线的函数表达式.
(2)若点P在第二象限内,且PE=OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【参考答案】
1.
B
2.A [解析]∵二次函数的图象与x轴有交点,
∴Δ=b2-4ac=(-1)2-4×m-1≥0,解得m≤5.
故选A.
3.
C [解析]当x=0时,y=-x2+4x-4=-4,则抛物线与y轴的交点坐标为(0,-4),
当y=0时,-x2+4x-4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),
所以抛物线与坐标轴有2个交点.故选C.
4.D [解析]∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为直线x=-1,
∴二次函数的图象与x轴另一个交点为(-4,0),
∵a<0,∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是-45.D [解析]∵y=x2-4x+a=(x-2)2+(a-4),向左平移一个单位,再向上平移一个单位后的解析式为y=(x-1)2+(a-3).
令2=(x-1)2+(a-3),即x2-2x+a-4=0,由Δ=4-4(a-4)>0,得a<5.
6.D [解析]y=(x-a-1)(x-a+1)-3a+7=x2-2ax+a2-3a+6,
∵抛物线与x轴没有公共点,∴Δ=(-2a)2-4(a2-3a+6)<0,解得a<2.
∵抛物线的对称轴为直线x=-=a,抛物线开口向上,而当x<-1时,y随x的增大而减小,
∴a≥-1,∴实数a的取值范围是-1≤a<2.故选D.
7.A [解析]关于x的一元二次方程(x+1)(x-2)-m=0的解为x1,x2,可以看作二次函数m=(x+1)(x-2)的图象与x轴交点的横坐标,
∵二次函数m=(x+1)(x-2)的图象与x轴交点坐标为(-1,0),(2,0),如图:
当m>0时,就是抛物线位于x轴上方的部分,此时x<-1,或x>2.
又∵x1∴x1<-1,x2>2,
∴x1<-1<2故选A.
8.C [解析]先把两个函数化成一般形式,若为二次函数,计算当y=0时,关于x的一元二次方程根的判别式,从而确定图象与x轴的交点个数,若为一次函数,则与x轴只有一个交点,据此解答.∵y=(x+a)(x+b)=x2+(a+b)x+ab,∴Δ=(a+b)2-4ab,又∵a≠b,(a+b)2-4ab=(a-b)2>0,∴函数y=(x+a)(x+b)的图象与x轴有2个交点,∴M=2.∵函数y=(ax+1)(bx+1)=abx2+(a+b)x+1,∴当a≠b,ab≠0时,(a+b)2-4ab=(a-b)2>0,函数y=(ax+1)(bx+1)的图象与x轴有2个交点,即N=2,此时M=N;
当ab=0时,不妨令a=0,∵a≠b,∴b≠0,函数y=(ax+1)(bx+1)=bx+1为一次函数,与x轴有一个交点,即N=1,此时M=N+1.综上可知,M=N或M=N+1.故选C.
9.y=3(x+2)2-1
10.x1=-2,x2=1 [解析]∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),∴的解为即方程ax2=bx+c的解是x1=-2,x2=1.
11.k<4 [解析]∵二次函数y=x2-4x+k的图象的顶点在x轴下方,
∴二次函数y=x2-4x+k的图象与x轴有两个公共点.
∴b2-4ac>0,即(-4)2-4×1×k>0.解得
k<4.
12.00,解得m<.
当直线y=x+m经过原点时与函数y=的图象有两个不同的交点,再向上平移,有三个交点,∴m>0,∴m的取值范围为013.解:(1)根据甲同学的错误可知x=0时,y=c=3是正确的,
由甲同学提供的数据,选择x=-1,y=6;x=1,y=2代入y=ax2+bx+3,得解得a=1是正确的.
根据乙同学提供的数据,选择x=-1,y=-2;x=1,y=2代入y=x2+bx+c,
得解得b=2是正确的,
∴y=x2+2x+3.
(2)≥-1 [解析]抛物线y=x2+2x+3的对称轴为直线x=-1,
∵二次项系数为1,故抛物线开口向上,
∴当x≥-1时,y的值随x值的增大而增大.
故答案为≥-1.
(3)∵方程ax2+bx+c=k(a≠0)有两个不相等的实数根,
即x2+2x+3-k=0有两个不相等的实数根,
∴Δ=4-4(3-k)>0,
解得k>2.
14.解:(1)2 [解析]∵二次函数y=-x2+bx+3的图象过点A(-1,0),
∴0=-(-1)2-b+3.
∴b=2.
故填2.
(2)如图①,连接BD,BC,过点P作PH⊥x轴于点H,分别交BC,BD于点M,N.
由题意知,抛物线y=-x2+2x+3交x轴于点A(-1,0),B(3,0),交y轴于点C(0,3),且点D为OC的中点,
∴D0,.
易求直线BC的解析式为y=-x+3,
直线BD的解析式为y=-x+.
假设存在符合条件的点P(m,-m2+2m+3),
则M(m,-m+3),Nm,-m+.
∵PM=MN=NH,
∴-m+=(-m2+2m+3)-(-m+3).
整理,得2m2-7m+3=0,
解得m1=,m2=3(不合题意,舍去).
∴P,使得PM=MN=NH.
15.[分析]
(1)根据点A(2,0)、抛物线对称轴,可得点B(-4,0),则可设函数表达式为:y=a(x-2)(x+4),根据点C(0,-2),即可求解;
(2)设出点D坐标,表示出PE的长,根据PE=OD,求得:点D(-5,0),利用S△PBE=PE×BD即可求解;
(3)△BDM是以BD为腰的等腰三角形,则分BD=BM和BD=DM两种情况求解.
解:(1)由题意得点A的坐标是(2,0),抛物线的对称轴是直线x=-1,则点B(-4,0),
设函数表达式为:y=a(x-2)(x+4)=a(x2+2x-8),
将C(0,-2)的坐标代入,得-8a=-2,
解得:a=,
故抛物线的表达式为:y=x2+x-2.
(2)易得直线BC的表达式为:y=-x-2.
设点D(x,0),
则点Px,x2+x-2,点Ex,-x-2,
∵PE=OD,点P在直线BC上方,
∴PE=x2+x-2+x+2=(-x),
解得:x=0或-5(舍去x=0),则点D(-5,0).
故S△PBE=×PE×BD=OD×BD=×1=.
(3)由题意得△BDM是以BD为腰的等腰三角形,存在:BD=BM和BD=DM两种情况,
易得BD=1.
①当BD=BM,M点在线段CB的延长线上时,过点M作MH⊥x轴于点H,
易得△MHB∽△COB,则=,
即=,解得MH=.
令y=-x-2=,解得x=-,
故点M.
②当BD=DM'时,
设点M',其中x<-4.则M'D2=[x-(-5)]2+=1.
整理得x2+x+=0.
解得x1=-4(舍去),x2=-.
当x=-时,-x-2=.故点M'.
综上所述,点M坐标为或.
九年级数学上册
22.1
二次函数的图象及其性质
同步测试(含答案)
1.
已知抛物线c:y=x2+2x-3,将抛物线c平移得到抛物线c',如果两条抛物线关于直线x=1对称,那么下列说法正确的是
( )
A.将抛物线c沿x轴向右平移个单位得到抛物线c'
B.将抛物线c沿x轴向右平移4个单位得到抛物线c'
C.将抛物线c沿x轴向右平移个单位得到抛物线c'
D.将抛物线c沿x轴向右平移6个单位得到抛物线c'
2.已知二次函数y=x2-x+m-1的图象与x轴有交点,则m的取值范围是
( )
A.m≤5
B.m≥2
C.m<5
D.m>2
3.
抛物线y=-x2+4x-4与坐标轴的交点个数为
( )
A.0
B.1
C.2
D.3
4.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为直线x=-1,则使函数值y>0成立的x的取值范围是
( )
A.x<-4或x>2
B.-4≤x≤2
C.x≤-4或x≥2
D.-4
( )
A.a>3
B.a<3
C.a>5
D.a<5
6.已知二次函数y=(x-a-1)(x-a+1)-3a+7(其中x是自变量)的图象与x轴没有公共点,且当x<-1时,y随x的增大而减小,则实数a的取值范围是
( )
A.a<2
B.a>-1
C.-1
7.已知m>0,关于x的一元二次方程(x+1)(x-2)-m=0的解为x1,x2(x1
A.x1<-1<2
( )
A.M=N-1或M=N+1
B.M=N-1或M=N+2
C.M=N或M=N+1
D.M=N或M=N-1
9.将抛物线y=3(x+1)2-2向上平移1个单位,再向左平移1个单位得到的抛物线的解析式是 .?
10.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则方程ax2=bx+c的解是 .?
11.已知二次函数y=x2-4x+k的图象的顶点在x轴下方,则实数k的取值范围是 .?
12.已知函数y=的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为 .?
13.在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下:
x
…
-1
0
1
2
3
…
y甲
…
6
3
2
3
6
…
乙写错了常数项,列表如下:
x
…
-1
0
1
2
3
…
y乙
…
-2
-1
2
7
14
…
通过上述信息,解决以下问题:
(1)求原二次函数y=ax2+bx+c(a≠0)的表达式;
(2)对于二次函数y=ax2+bx+c(a≠0),当x 时,y的值随x的值增大而增大;?
(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,求k的取值范围.
14.
如图,二次函数y=-x2+bx+3的图象与x轴交于点A,B,与y轴交于点C,点A的坐标为(-1,0),点D为OC的中点,点P在抛物线上.
(1)b= .?
(2)若点P在第一象限,过点P作PH⊥x轴,垂足为H,PH与BC,BD分别交于点M,N.是否存在这样的点P,使得PM=MN=NH,若存在,求出点P的坐标;若不存在,请说明理由.
15.如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,-2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.
(1)求抛物线的函数表达式.
(2)若点P在第二象限内,且PE=OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【参考答案】
1.
B
2.A [解析]∵二次函数的图象与x轴有交点,
∴Δ=b2-4ac=(-1)2-4×m-1≥0,解得m≤5.
故选A.
3.
C [解析]当x=0时,y=-x2+4x-4=-4,则抛物线与y轴的交点坐标为(0,-4),
当y=0时,-x2+4x-4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),
所以抛物线与坐标轴有2个交点.故选C.
4.D [解析]∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为直线x=-1,
∴二次函数的图象与x轴另一个交点为(-4,0),
∵a<0,∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是-4
令2=(x-1)2+(a-3),即x2-2x+a-4=0,由Δ=4-4(a-4)>0,得a<5.
6.D [解析]y=(x-a-1)(x-a+1)-3a+7=x2-2ax+a2-3a+6,
∵抛物线与x轴没有公共点,∴Δ=(-2a)2-4(a2-3a+6)<0,解得a<2.
∵抛物线的对称轴为直线x=-=a,抛物线开口向上,而当x<-1时,y随x的增大而减小,
∴a≥-1,∴实数a的取值范围是-1≤a<2.故选D.
7.A [解析]关于x的一元二次方程(x+1)(x-2)-m=0的解为x1,x2,可以看作二次函数m=(x+1)(x-2)的图象与x轴交点的横坐标,
∵二次函数m=(x+1)(x-2)的图象与x轴交点坐标为(-1,0),(2,0),如图:
当m>0时,就是抛物线位于x轴上方的部分,此时x<-1,或x>2.
又∵x1
∴x1<-1<2
8.C [解析]先把两个函数化成一般形式,若为二次函数,计算当y=0时,关于x的一元二次方程根的判别式,从而确定图象与x轴的交点个数,若为一次函数,则与x轴只有一个交点,据此解答.∵y=(x+a)(x+b)=x2+(a+b)x+ab,∴Δ=(a+b)2-4ab,又∵a≠b,(a+b)2-4ab=(a-b)2>0,∴函数y=(x+a)(x+b)的图象与x轴有2个交点,∴M=2.∵函数y=(ax+1)(bx+1)=abx2+(a+b)x+1,∴当a≠b,ab≠0时,(a+b)2-4ab=(a-b)2>0,函数y=(ax+1)(bx+1)的图象与x轴有2个交点,即N=2,此时M=N;
当ab=0时,不妨令a=0,∵a≠b,∴b≠0,函数y=(ax+1)(bx+1)=bx+1为一次函数,与x轴有一个交点,即N=1,此时M=N+1.综上可知,M=N或M=N+1.故选C.
9.y=3(x+2)2-1
10.x1=-2,x2=1 [解析]∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),∴的解为即方程ax2=bx+c的解是x1=-2,x2=1.
11.k<4 [解析]∵二次函数y=x2-4x+k的图象的顶点在x轴下方,
∴二次函数y=x2-4x+k的图象与x轴有两个公共点.
∴b2-4ac>0,即(-4)2-4×1×k>0.解得
k<4.
12.0
当直线y=x+m经过原点时与函数y=的图象有两个不同的交点,再向上平移,有三个交点,∴m>0,∴m的取值范围为0
由甲同学提供的数据,选择x=-1,y=6;x=1,y=2代入y=ax2+bx+3,得解得a=1是正确的.
根据乙同学提供的数据,选择x=-1,y=-2;x=1,y=2代入y=x2+bx+c,
得解得b=2是正确的,
∴y=x2+2x+3.
(2)≥-1 [解析]抛物线y=x2+2x+3的对称轴为直线x=-1,
∵二次项系数为1,故抛物线开口向上,
∴当x≥-1时,y的值随x值的增大而增大.
故答案为≥-1.
(3)∵方程ax2+bx+c=k(a≠0)有两个不相等的实数根,
即x2+2x+3-k=0有两个不相等的实数根,
∴Δ=4-4(3-k)>0,
解得k>2.
14.解:(1)2 [解析]∵二次函数y=-x2+bx+3的图象过点A(-1,0),
∴0=-(-1)2-b+3.
∴b=2.
故填2.
(2)如图①,连接BD,BC,过点P作PH⊥x轴于点H,分别交BC,BD于点M,N.
由题意知,抛物线y=-x2+2x+3交x轴于点A(-1,0),B(3,0),交y轴于点C(0,3),且点D为OC的中点,
∴D0,.
易求直线BC的解析式为y=-x+3,
直线BD的解析式为y=-x+.
假设存在符合条件的点P(m,-m2+2m+3),
则M(m,-m+3),Nm,-m+.
∵PM=MN=NH,
∴-m+=(-m2+2m+3)-(-m+3).
整理,得2m2-7m+3=0,
解得m1=,m2=3(不合题意,舍去).
∴P,使得PM=MN=NH.
15.[分析]
(1)根据点A(2,0)、抛物线对称轴,可得点B(-4,0),则可设函数表达式为:y=a(x-2)(x+4),根据点C(0,-2),即可求解;
(2)设出点D坐标,表示出PE的长,根据PE=OD,求得:点D(-5,0),利用S△PBE=PE×BD即可求解;
(3)△BDM是以BD为腰的等腰三角形,则分BD=BM和BD=DM两种情况求解.
解:(1)由题意得点A的坐标是(2,0),抛物线的对称轴是直线x=-1,则点B(-4,0),
设函数表达式为:y=a(x-2)(x+4)=a(x2+2x-8),
将C(0,-2)的坐标代入,得-8a=-2,
解得:a=,
故抛物线的表达式为:y=x2+x-2.
(2)易得直线BC的表达式为:y=-x-2.
设点D(x,0),
则点Px,x2+x-2,点Ex,-x-2,
∵PE=OD,点P在直线BC上方,
∴PE=x2+x-2+x+2=(-x),
解得:x=0或-5(舍去x=0),则点D(-5,0).
故S△PBE=×PE×BD=OD×BD=×1=.
(3)由题意得△BDM是以BD为腰的等腰三角形,存在:BD=BM和BD=DM两种情况,
易得BD=1.
①当BD=BM,M点在线段CB的延长线上时,过点M作MH⊥x轴于点H,
易得△MHB∽△COB,则=,
即=,解得MH=.
令y=-x-2=,解得x=-,
故点M.
②当BD=DM'时,
设点M',其中x<-4.则M'D2=[x-(-5)]2+=1.
整理得x2+x+=0.
解得x1=-4(舍去),x2=-.
当x=-时,-x-2=.故点M'.
综上所述,点M坐标为或.
同课章节目录
