人教版数学八年级上册13.3.2第1课时:等边三角形的性质与判定课件(23张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.3.2第1课时:等边三角形的性质与判定课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 386.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 15:55:47 | ||
图片预览







文档简介
(共23张PPT)
知识复习
1.什么是等边三角形?
A
B
C
三条边都相等的三角形是等边三角形
等边三角形是特殊的等腰三角形
知识复习
2.等腰三角形的特殊性质?
从边的角度:两腰相等;
从角的角度:等边对等角;
从对称性的角度:轴对称图形、三线合一。
顶角平分线、底边上的中线,底边上的高相互重合
等边三角形——性质
类比探究
根据等腰三角形的性质,你能填出等边三角形对应的结论吗?
图形
边
角
轴对称图形
等腰
三角形
两边相等
(定义)
两底角相等
(等边对等角)
是(三线合一)
一条对称轴
等边
三角形
三个内角都相等
每个角都等于60°
是(三线合一)
三条对称轴
三边相等
(定义)
你能证明这些结论吗?
类比探究
Eg.已知:△ABC
是等边三角形
求证:∠A
=∠B
=∠C
=60°.
A
B
C
证明:∵ △ABC
是等边三角形,
∴ BC
=AC,BC
=AB
∴ ∠A
=∠B,∠A
=∠C
∴ ∠A
=∠B
=∠C
∵ ∠A
+∠B
+∠C
=180°
∴ ∠A
=60°
∴ ∠A
=∠B
=∠C
=60°
类比探究
性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
由上例证明可得
几何语言:
∵ △ABC
是等边三角形,
∴ ∠A
=∠B
=∠C
=60°
A
B
C
类比探究
Eg.已知:△ABC
是等边三角形,AD⊥CB
求证:BD=CD,∠BAD=∠CAD.
证明:∵ △ABC
是等边三角形,
∴ ∠A
=∠B
=∠C
=60°
在△ABD与△ACD中,
∠B=∠C
∠ADB=∠ADC
AD=AD
∴
△ABD≌△ACD(AAS)
∴
BD=CD,
∠BAD=∠CAD
同理可得,CF,BE也遵循三线合一
A
B
C
D
E
F
类比探究
性质:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
由上例证明可得
几何语言:
∵ △ABC
是等边三角形,
AD⊥CB
∴ BD=CD,
∠BAD=∠CAD
或 ∵ △ABC
是等边三角形,
BD=CD
∴ AD⊥CB,
∠BAD=∠CAD
或 ∵ △ABC
是等边三角形,
∠BAD=∠CAD
∴ BD=CD,
AD⊥CB
A
B
C
D
类比探究
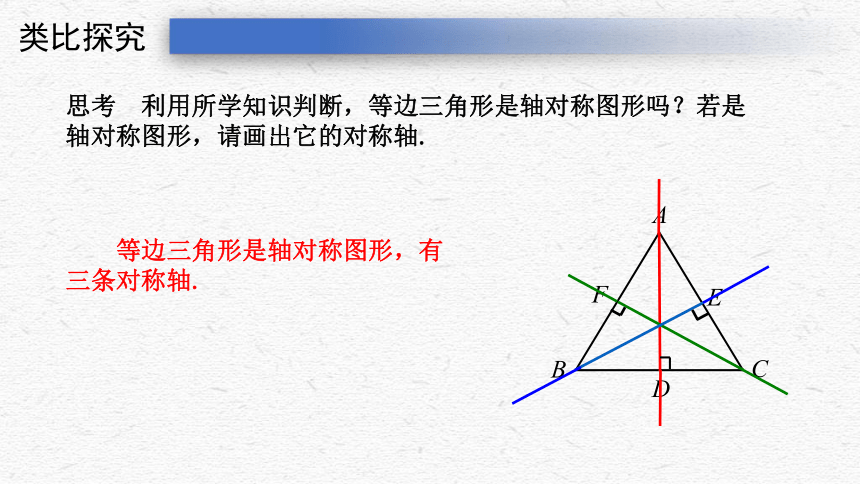
思考 利用所学知识判断,等边三角形是轴对称图形吗?若是
轴对称图形,请画出它的对称轴.
等边三角形是轴对称图形,有三条对称轴.
A
B
C
D
E
F
知识小结
等边三角形的性质:
1.等边三角形三条边相等.
2.等边三角形的三个内角都相等,并且每一个角都等于60°.
3.等边三角形每条边上的中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形,有三条对称轴.
随堂小测
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
4.如图,已知等边三角形ABC的周长为18?cm,△ADE是等边三角形,EC=2?cm,则△ADE的周长为________.
等边
60
3
12cm
等边三角形——判定
类比探究
问题 类比等腰三角形的判定,一个三角形满足什么条件就是等边三角形?
一般三角形
等边三角形
等腰三角形
思考1 一个三角形的三个内角满足什么条件是等边三角形?
思考2 一个等腰三角形的内角满足什么条件是等边三角形?
类比探究
Eg.
如图,已知:在△ABC
中,∠A=∠B=∠C.求证:△ABC
是等边三角形.
证明:∵ ∠A
=∠B=∠C
,
∴ BC
=AC,
AC
=AB.
∴ AB
=BC
=AC.
∴ △ABC
是等边三角形.
C
A
B
类比探究
判定定理1:
三个角都相等的三角形是等边三角形.
由上例证明可得
几何语言:
∵ ∠A
=∠B=∠C
∴ △ABC
是等边三角形
A
B
C
类比探究
Eg.已知:在△ABC
中,AC
=BC且∠A
=60°.
求证:(1)△ABC是等边三角形吗?为什么?
(2)如果“∠A=60°”改为“∠B=60°”或“∠C=60°”结论还成立吗?
证明:∵
AC=BC,
C
A
B
∴
∠A=∠B=60°.
在△ABC中,∠C=180°-∠A-∠B
=180°-60°-60°
=60°
∴
∠A=∠B=∠C=60°.
∴
△ABC是等边三角形.
成立
类比探究
判定定理2:
有一个角是60°的等腰三角形是等边三角形.
由上例证明可得
几何语言:
在△ABC
中,
∵ BC
=AC,∠A
=60°(或∠B=60°或∠C=60°)
∴ △ABC
是等边三角形.
A
B
C
D
知识小结
等边三角形的判定:
判定定理1:
三个角都相等的三角形是等边三角形。
判定定理2:
有一个角是60°的等腰三角形是等边三角形。
随堂小测
1、已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为________.
2、△ABC是等腰三角形,周长为15cm,且∠A=60°,则BC
=_______.
9
5
3、如图,过等边△ABC的顶点A作线段AD,若∠1=20°,则∠2的度数是( )
A.100°
B.80°
C.60°
D.40°
B
C
A
B
1
2
D
随堂小测
4、如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
于点D,E.求证:△ADE
是等边三角形.
证明:
∵ △ABC
是等边三角形,
∴ ∠A
=∠B
=∠C
=60°.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠A=∠ADE
=∠AED.
∴ △ADE
是等边三角形.
A
B
C
D
E
随堂小测
变式1 若点D、E
在边AB、AC
的延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC
是等边三角形,
∴ ∠A
=∠ABC
=∠ACB
=60°.
∵ DE∥BC,
∴ ∠ABC
=∠ADE,
∠ACB
=∠AED.
∴ ∠A
=∠ADE
=∠AED.
∴ △ADE
是等边三角形.
A
D
E
B
C
随堂小测
变式2 若点D、E
在边AB、AC
的反向延长线上,且DE∥BC,结论依然成立吗?
证明:
∵ △ABC
是等边三角形,
∴ ∠BAC
=∠B
=∠C
=60°.
∵ DE∥BC,
∴ ∠B
=∠D,∠C
=∠E.
∴ ∠EAD
=∠D
=∠E.
∴ △ADE
是等边三角形.
A
D
E
B
C
THANKS
谢谢观看!
知识复习
1.什么是等边三角形?
A
B
C
三条边都相等的三角形是等边三角形
等边三角形是特殊的等腰三角形
知识复习
2.等腰三角形的特殊性质?
从边的角度:两腰相等;
从角的角度:等边对等角;
从对称性的角度:轴对称图形、三线合一。
顶角平分线、底边上的中线,底边上的高相互重合
等边三角形——性质
类比探究
根据等腰三角形的性质,你能填出等边三角形对应的结论吗?
图形
边
角
轴对称图形
等腰
三角形
两边相等
(定义)
两底角相等
(等边对等角)
是(三线合一)
一条对称轴
等边
三角形
三个内角都相等
每个角都等于60°
是(三线合一)
三条对称轴
三边相等
(定义)
你能证明这些结论吗?
类比探究
Eg.已知:△ABC
是等边三角形
求证:∠A
=∠B
=∠C
=60°.
A
B
C
证明:∵ △ABC
是等边三角形,
∴ BC
=AC,BC
=AB
∴ ∠A
=∠B,∠A
=∠C
∴ ∠A
=∠B
=∠C
∵ ∠A
+∠B
+∠C
=180°
∴ ∠A
=60°
∴ ∠A
=∠B
=∠C
=60°
类比探究
性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
由上例证明可得
几何语言:
∵ △ABC
是等边三角形,
∴ ∠A
=∠B
=∠C
=60°
A
B
C
类比探究
Eg.已知:△ABC
是等边三角形,AD⊥CB
求证:BD=CD,∠BAD=∠CAD.
证明:∵ △ABC
是等边三角形,
∴ ∠A
=∠B
=∠C
=60°
在△ABD与△ACD中,
∠B=∠C
∠ADB=∠ADC
AD=AD
∴
△ABD≌△ACD(AAS)
∴
BD=CD,
∠BAD=∠CAD
同理可得,CF,BE也遵循三线合一
A
B
C
D
E
F
类比探究
性质:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
由上例证明可得
几何语言:
∵ △ABC
是等边三角形,
AD⊥CB
∴ BD=CD,
∠BAD=∠CAD
或 ∵ △ABC
是等边三角形,
BD=CD
∴ AD⊥CB,
∠BAD=∠CAD
或 ∵ △ABC
是等边三角形,
∠BAD=∠CAD
∴ BD=CD,
AD⊥CB
A
B
C
D
类比探究
思考 利用所学知识判断,等边三角形是轴对称图形吗?若是
轴对称图形,请画出它的对称轴.
等边三角形是轴对称图形,有三条对称轴.
A
B
C
D
E
F
知识小结
等边三角形的性质:
1.等边三角形三条边相等.
2.等边三角形的三个内角都相等,并且每一个角都等于60°.
3.等边三角形每条边上的中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形,有三条对称轴.
随堂小测
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
4.如图,已知等边三角形ABC的周长为18?cm,△ADE是等边三角形,EC=2?cm,则△ADE的周长为________.
等边
60
3
12cm
等边三角形——判定
类比探究
问题 类比等腰三角形的判定,一个三角形满足什么条件就是等边三角形?
一般三角形
等边三角形
等腰三角形
思考1 一个三角形的三个内角满足什么条件是等边三角形?
思考2 一个等腰三角形的内角满足什么条件是等边三角形?
类比探究
Eg.
如图,已知:在△ABC
中,∠A=∠B=∠C.求证:△ABC
是等边三角形.
证明:∵ ∠A
=∠B=∠C
,
∴ BC
=AC,
AC
=AB.
∴ AB
=BC
=AC.
∴ △ABC
是等边三角形.
C
A
B
类比探究
判定定理1:
三个角都相等的三角形是等边三角形.
由上例证明可得
几何语言:
∵ ∠A
=∠B=∠C
∴ △ABC
是等边三角形
A
B
C
类比探究
Eg.已知:在△ABC
中,AC
=BC且∠A
=60°.
求证:(1)△ABC是等边三角形吗?为什么?
(2)如果“∠A=60°”改为“∠B=60°”或“∠C=60°”结论还成立吗?
证明:∵
AC=BC,
C
A
B
∴
∠A=∠B=60°.
在△ABC中,∠C=180°-∠A-∠B
=180°-60°-60°
=60°
∴
∠A=∠B=∠C=60°.
∴
△ABC是等边三角形.
成立
类比探究
判定定理2:
有一个角是60°的等腰三角形是等边三角形.
由上例证明可得
几何语言:
在△ABC
中,
∵ BC
=AC,∠A
=60°(或∠B=60°或∠C=60°)
∴ △ABC
是等边三角形.
A
B
C
D
知识小结
等边三角形的判定:
判定定理1:
三个角都相等的三角形是等边三角形。
判定定理2:
有一个角是60°的等腰三角形是等边三角形。
随堂小测
1、已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为________.
2、△ABC是等腰三角形,周长为15cm,且∠A=60°,则BC
=_______.
9
5
3、如图,过等边△ABC的顶点A作线段AD,若∠1=20°,则∠2的度数是( )
A.100°
B.80°
C.60°
D.40°
B
C
A
B
1
2
D
随堂小测
4、如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
于点D,E.求证:△ADE
是等边三角形.
证明:
∵ △ABC
是等边三角形,
∴ ∠A
=∠B
=∠C
=60°.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠A=∠ADE
=∠AED.
∴ △ADE
是等边三角形.
A
B
C
D
E
随堂小测
变式1 若点D、E
在边AB、AC
的延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC
是等边三角形,
∴ ∠A
=∠ABC
=∠ACB
=60°.
∵ DE∥BC,
∴ ∠ABC
=∠ADE,
∠ACB
=∠AED.
∴ ∠A
=∠ADE
=∠AED.
∴ △ADE
是等边三角形.
A
D
E
B
C
随堂小测
变式2 若点D、E
在边AB、AC
的反向延长线上,且DE∥BC,结论依然成立吗?
证明:
∵ △ABC
是等边三角形,
∴ ∠BAC
=∠B
=∠C
=60°.
∵ DE∥BC,
∴ ∠B
=∠D,∠C
=∠E.
∴ ∠EAD
=∠D
=∠E.
∴ △ADE
是等边三角形.
A
D
E
B
C
THANKS
谢谢观看!
