第二章 直角三角形的边角关系单元测试题(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系单元测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二单元测试题
(时间:45分钟 满分:100分)
一、选择题(每题5分,共25分)
1.如图所示,梯子与地面的夹角为a,关于∠a的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A.cosa的值越大,梯子越陡
B.sina的值越大,梯子越陡
C.tana的值越小,梯子越陡
D.梯子的陡缓程度与∠a的三角函数值无关
2.在△ABC中,若,则∠C的度数是( )
A. 45° B. 60° C. 75° D. 105°
3.如图所示,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11-2)米 B.(11-2)米 C.(11-2)米 D.(11-4)米
4.如图所示,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
26米 B. 28米 C. 30米 D. 46米
第4题图 第5题图
5.如图所示,在某监测点B处望见北东一艘正在作业的渔船在南偏西15°方向上的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则BC之间的距离为( )
A. 20海里 B. 10海里 C. 20海里 D. 30海里
二、填空题(每题5分,共25分)
6.在Rt△ABC中,∠C=90°,如果sinA=,则cos的值为____________。
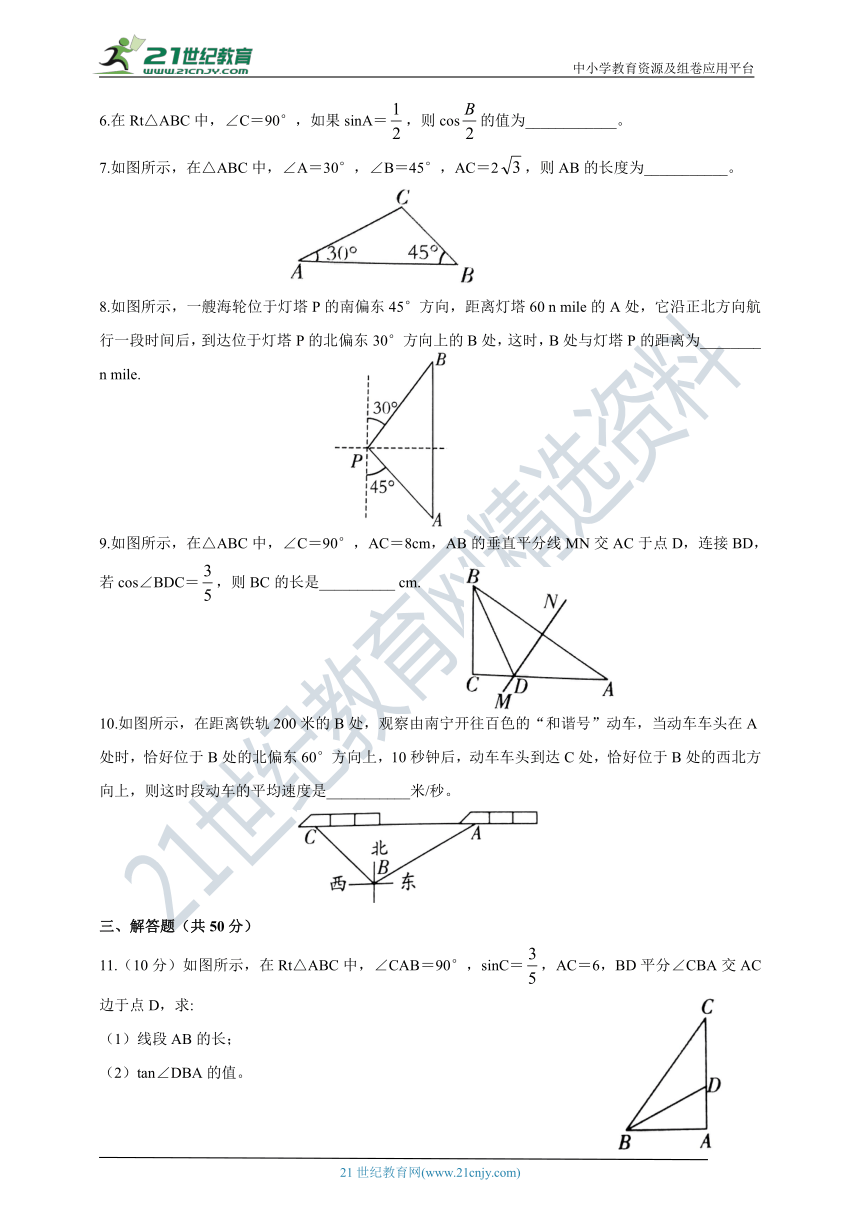
7.如图所示,在△ABC中,∠A=30°,∠B=45°,AC=2,则AB的长度为___________。
8.如图所示,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60 n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为________
n mile.
9.如图所示,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于点D,连接BD,若cos∠BDC=,则BC的长是__________ cm.
10.如图所示,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上,10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是___________米/秒。
三、解答题(共50分)
11.(10分)如图所示,在Rt△ABC中,∠CAB=90°,sinC=,AC=6,BD平分∠CBA交AC边于点D,求:
(1)线段AB的长;
(2)tan∠DBA的值。
12.(10分)如图所示,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520 km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数,参考数据:sin67°≈,cos67°≈,tan67°≈,≈1.73)
13.(15分)如图所示,在小山的东侧A村有一热气球,由于受西风的影响,以每分钟35m的速度沿
着与水平方向成75°角的方向飞行,40分钟时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B村在一条直线上,同时测得B村的俯角为30°又在A村测得山顶P的仰角为45°,求A村与B村的距离及山高.(精确到0.1m.参考数据:≈1.414,≈1.732)
14.(15分)如图所示,建筑物C在观测点A的北偏东65°方向上,从观测点A出发向南偏东40°方向走了130m到达观测点B,此时测得建筑物C在观测点B的北偏东20°方向上,求观测点B与建筑物C之间的距离.(结果精确到0.1m.参考数据:3≈1.73)
参考答案
一,选择题
1,B 2,C 3,D 4,D 5,C
二,填空题
6. 7. 3+ 8. 60 9. 4 10. 20(+1)
三、解答题
11,解,(1)∵在Rt△ABC中,∠CAB=90?,∴ sinC==,.
可设AB=3k,则BC=5k,∵AC=6,∴,∴或(舍去)。
∴AB=3×;
(2)如图所示,过点D作DE⊥BC于点E.设AD=x,则CD=6-x,
∵BD平分∠CBA交AC边于点D,∠CAB=90°,∴DE=AD=x.
在Rt△BDE与Rt△BDA中,,Rt△BDE≌ Rt△BDA(HL).
∴BE=BA=。∴CE=BC-BE=5×-=3.
在Rt△CDE中,∵∠CED=90?,DE2+CE2=CD2.
∴x2+32=(6-x)2,解得。∴AD=。
∴tan∠DBA=== .
12.解:如图所示,过点B作BD⊥AC于点D.
∵B地位于A地北偏东67?方向,距离A地520 km,∴∠ABD=67?.
∴AD=AB sin67?=520× =480(km).
BD=AB? cos67?=520×=200(km)。
∵ C地位于B地南偏东30?方向,∴∠CBD=30?.
∴CD=BD· tan30?=200×=(km).
∴AC=AD+CD=480+≈480+115=595(km).
答:A地到C地之间高铁线路的长约为595 km.
13,解:如图所示,过点A作AD⊥BC于点D.
在Rt△ADC中,∠ACD=75?-30?=45?,AC=35×40=1 400(m),
∴AD=AC· sin45?=1 400×=700(m).
在Rt△ABD中,∠B=30?.∴AB=2AD=1 400≈1 979.6(m).
过点P作PE⊥AB于点E,则AE=PE, BE=PE.
∴(+1)PE≈1 979.6,PE≈≈724.6(m).
答:A村与B村的距离约为1979.6m,山高约为724.6 m.
14,解:如图所示,过点A作AD⊥BC于点D.
由题意得,∠ABC= 40?+20?=60?, AB=130 m, ∠BAD=30?.
在Rt△ADB中,∵∠DAB=30?,∴DB=AB=×130=65(m),AD=BD=65(m).
∵∠BAC=180?-65?-40?=75?,∴∠C=180°-∠ABC-∠BAC=180°-60?-75°=45°.
在Rt△ADC中,∵tanC==1,∴CD=AD=65(m).
∴BC=BD+CD=65+65≈177.5(m)。
答:观测点B与建筑物C之间的距离约为177.5 m.
_21?????????è?????(www.21cnjy.com)_
第二单元测试题
(时间:45分钟 满分:100分)
一、选择题(每题5分,共25分)
1.如图所示,梯子与地面的夹角为a,关于∠a的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A.cosa的值越大,梯子越陡
B.sina的值越大,梯子越陡
C.tana的值越小,梯子越陡
D.梯子的陡缓程度与∠a的三角函数值无关
2.在△ABC中,若,则∠C的度数是( )
A. 45° B. 60° C. 75° D. 105°
3.如图所示,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11-2)米 B.(11-2)米 C.(11-2)米 D.(11-4)米
4.如图所示,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
26米 B. 28米 C. 30米 D. 46米
第4题图 第5题图
5.如图所示,在某监测点B处望见北东一艘正在作业的渔船在南偏西15°方向上的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则BC之间的距离为( )
A. 20海里 B. 10海里 C. 20海里 D. 30海里
二、填空题(每题5分,共25分)
6.在Rt△ABC中,∠C=90°,如果sinA=,则cos的值为____________。
7.如图所示,在△ABC中,∠A=30°,∠B=45°,AC=2,则AB的长度为___________。
8.如图所示,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60 n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为________
n mile.
9.如图所示,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于点D,连接BD,若cos∠BDC=,则BC的长是__________ cm.
10.如图所示,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上,10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是___________米/秒。
三、解答题(共50分)
11.(10分)如图所示,在Rt△ABC中,∠CAB=90°,sinC=,AC=6,BD平分∠CBA交AC边于点D,求:
(1)线段AB的长;
(2)tan∠DBA的值。
12.(10分)如图所示,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520 km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数,参考数据:sin67°≈,cos67°≈,tan67°≈,≈1.73)
13.(15分)如图所示,在小山的东侧A村有一热气球,由于受西风的影响,以每分钟35m的速度沿
着与水平方向成75°角的方向飞行,40分钟时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B村在一条直线上,同时测得B村的俯角为30°又在A村测得山顶P的仰角为45°,求A村与B村的距离及山高.(精确到0.1m.参考数据:≈1.414,≈1.732)
14.(15分)如图所示,建筑物C在观测点A的北偏东65°方向上,从观测点A出发向南偏东40°方向走了130m到达观测点B,此时测得建筑物C在观测点B的北偏东20°方向上,求观测点B与建筑物C之间的距离.(结果精确到0.1m.参考数据:3≈1.73)
参考答案
一,选择题
1,B 2,C 3,D 4,D 5,C
二,填空题
6. 7. 3+ 8. 60 9. 4 10. 20(+1)
三、解答题
11,解,(1)∵在Rt△ABC中,∠CAB=90?,∴ sinC==,.
可设AB=3k,则BC=5k,∵AC=6,∴,∴或(舍去)。
∴AB=3×;
(2)如图所示,过点D作DE⊥BC于点E.设AD=x,则CD=6-x,
∵BD平分∠CBA交AC边于点D,∠CAB=90°,∴DE=AD=x.
在Rt△BDE与Rt△BDA中,,Rt△BDE≌ Rt△BDA(HL).
∴BE=BA=。∴CE=BC-BE=5×-=3.
在Rt△CDE中,∵∠CED=90?,DE2+CE2=CD2.
∴x2+32=(6-x)2,解得。∴AD=。
∴tan∠DBA=== .
12.解:如图所示,过点B作BD⊥AC于点D.
∵B地位于A地北偏东67?方向,距离A地520 km,∴∠ABD=67?.
∴AD=AB sin67?=520× =480(km).
BD=AB? cos67?=520×=200(km)。
∵ C地位于B地南偏东30?方向,∴∠CBD=30?.
∴CD=BD· tan30?=200×=(km).
∴AC=AD+CD=480+≈480+115=595(km).
答:A地到C地之间高铁线路的长约为595 km.
13,解:如图所示,过点A作AD⊥BC于点D.
在Rt△ADC中,∠ACD=75?-30?=45?,AC=35×40=1 400(m),
∴AD=AC· sin45?=1 400×=700(m).
在Rt△ABD中,∠B=30?.∴AB=2AD=1 400≈1 979.6(m).
过点P作PE⊥AB于点E,则AE=PE, BE=PE.
∴(+1)PE≈1 979.6,PE≈≈724.6(m).
答:A村与B村的距离约为1979.6m,山高约为724.6 m.
14,解:如图所示,过点A作AD⊥BC于点D.
由题意得,∠ABC= 40?+20?=60?, AB=130 m, ∠BAD=30?.
在Rt△ADB中,∵∠DAB=30?,∴DB=AB=×130=65(m),AD=BD=65(m).
∵∠BAC=180?-65?-40?=75?,∴∠C=180°-∠ABC-∠BAC=180°-60?-75°=45°.
在Rt△ADC中,∵tanC==1,∴CD=AD=65(m).
∴BC=BD+CD=65+65≈177.5(m)。
答:观测点B与建筑物C之间的距离约为177.5 m.
_21?????????è?????(www.21cnjy.com)_
