2020秋沪科版八年级数学上册14.1 全等三角形习题课件(共16张PPT)
文档属性
| 名称 | 2020秋沪科版八年级数学上册14.1 全等三角形习题课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 16:29:40 | ||
图片预览



文档简介
(共16张PPT)
14.1 全等三角形
第14章 全等三角形
知识点1 全等形
1.下列说法正确的是(
C
)
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
2.由同一张底片冲洗出来的两张五寸照片的图案 是 全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片
不是 全等图形.(填“是”或“不是”)?
知识点2 全等三角形及对应元素
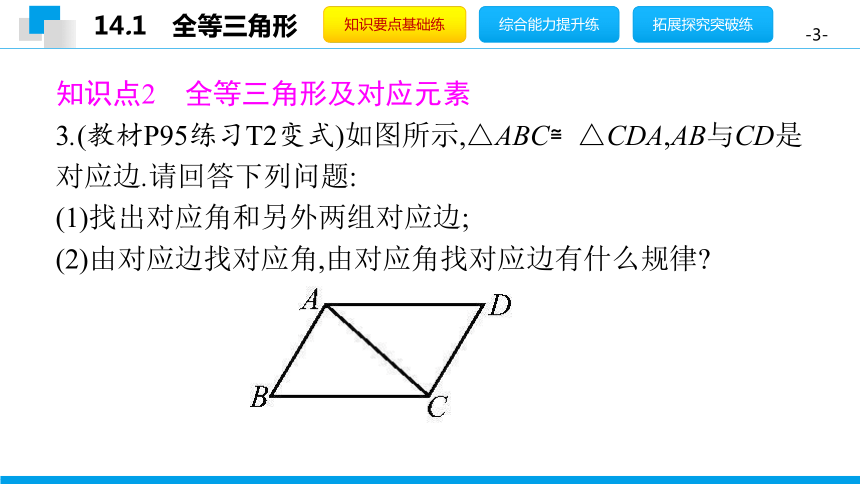
3.(教材P95练习T2变式)如图所示,△ABC≌△CDA,AB与CD是对应边.请回答下列问题:
(1)找出对应角和另外两组对应边;
(2)由对应边找对应角,由对应角找对应边有什么规律?
解:(1)对应角:∠BAC与∠DCA,∠ACB与∠CAD,∠B与∠D;
对应边:BC与DA,AC与CA.
(2)对应边所对的角是对应角,对应角所对的边是对应边.
知识点3 全等三角形的性质
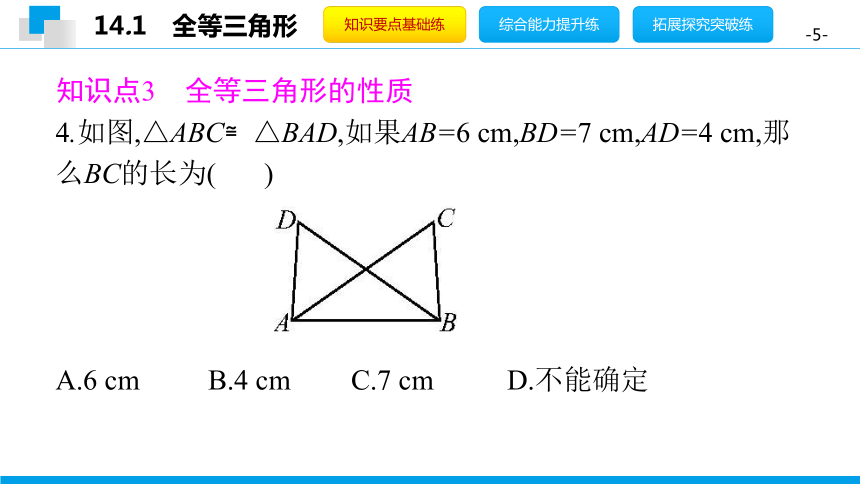
4.如图,△ABC≌△BAD,如果AB=6
cm,BD=7
cm,AD=4
cm,那么BC的长为(
B
)
?
?
?
?
A.6
cm
B.4
cm
C.7
cm
D.不能确定
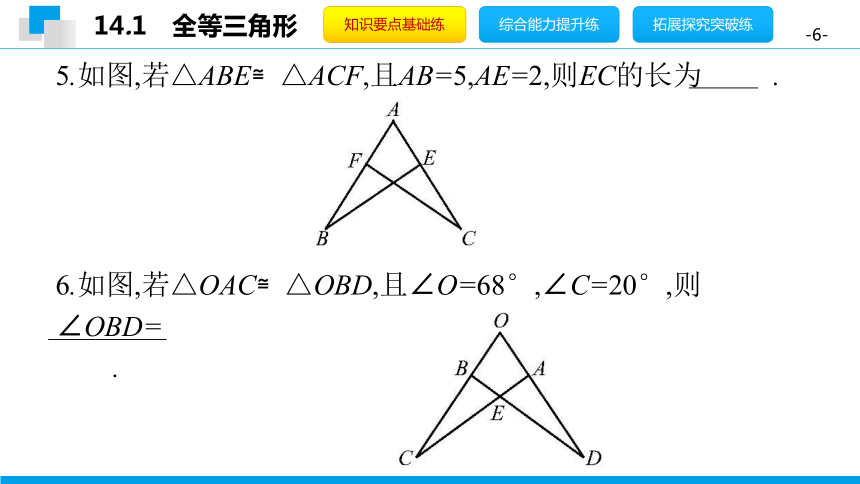
5.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为 3 .?
6.如图,若△OAC≌△OBD,且∠O=68°,∠C=20°,则∠OBD=92°
.?
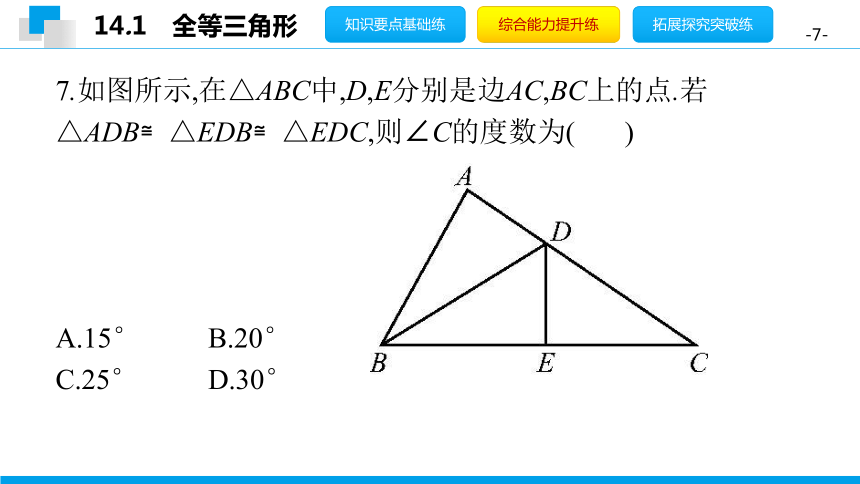
7.如图所示,在△ABC中,D,E分别是边AC,BC上的点.若△ADB≌△EDB≌△EDC,则∠C的度数为(
D
)
?
?
?
?
A.15°
B.20°
C.25°
D.30°
8.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于下列结论:
①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的个数是(
C
)
A.1
B.2
C.3
D.4
9.如图,∠C=∠CAM=90°,AC=8,BC=4,P,Q两点分别在线段AC和射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则AP的长度为 4或8 .?
10.(滁州期末)如图,已知△ABC≌△DCB,∠ABC=65°,
∠ACB=30°,则∠ACD= 35 °.?
【变式拓展】如图,△ABC≌△ADE,若∠B=80°,∠C=30°,
∠DAC=35°,则∠EAC的度数为(
B
)
?
A.40°
B.35°
C.30°
D.25°
11.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,
∠ACB=20°,则∠ADC的度数是 65° .?
12.一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,3x-2,2y+1.若这两个三角形全等,则x+y的值是
.?
13.如图,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
解:
(1)∵△ABE≌△ACD,∴BE=CD,
∴BE-DE=CD-DE,即BD=CE.
∵BE=6,DE=2,∴CE=BD=BE-DE=4,
∴BC=BE+CE=10.
(2)∵△ABE≌△ACD,∴∠BAE=∠CAD,
∴∠BAD=∠CAE=30°,
∴∠DAE=75°-30°-30°=15°.
14.如图,△ABD≌△EBC,AB=3
cm,BC=4.5
cm,点A,B,C在一条直线上.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
解:(1)∵△ABD≌△EBC,∴AB=EB,BD=BC,
∴DE=BD-BE=4.5-3=1.5(cm).
(2)AC⊥BD.
理由:∵△ABD≌△EBC,∴∠ABD=∠EBC.
又∵∠ABD+∠EBC=180°,
∴∠EBC=90°,∴AC⊥BD.
15.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,
∠EAB=105°,求∠BFD和∠BED的度数.
?
解:∵△ABC≌△ADE,∴∠CAB=∠EAD.
又∵∠CAD=35°,∠EAB=105°,
∠EAD+∠DAC+∠CAB=∠EAB=105°,
∴∠EAD=∠DAC=∠CAB=35°,
∴∠BFD=∠DAB+∠B=70°+20°=90°,
∠BED=∠BFD-∠D=90°-20°=70°.
16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)证明:BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
解:(1)∵△BAD≌△ACE,∴BD=AE,AD=CE,
又∵AE=AD+DE=CE+DE,∴BD=DE+CE.
(2)∵△BAD≌△ACE,∴∠ADB=∠CEA.
∵BD∥CE,∴∠CEA=∠BDE,∴∠ADB=∠BDE.
又∵∠ADB+∠BDE=180°,∴∠ADB=90°,
∴△ABD是∠ADB=90°的直角三角形时,BD∥CE.
14.1 全等三角形
第14章 全等三角形
知识点1 全等形
1.下列说法正确的是(
C
)
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
2.由同一张底片冲洗出来的两张五寸照片的图案 是 全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片
不是 全等图形.(填“是”或“不是”)?
知识点2 全等三角形及对应元素
3.(教材P95练习T2变式)如图所示,△ABC≌△CDA,AB与CD是对应边.请回答下列问题:
(1)找出对应角和另外两组对应边;
(2)由对应边找对应角,由对应角找对应边有什么规律?
解:(1)对应角:∠BAC与∠DCA,∠ACB与∠CAD,∠B与∠D;
对应边:BC与DA,AC与CA.
(2)对应边所对的角是对应角,对应角所对的边是对应边.
知识点3 全等三角形的性质
4.如图,△ABC≌△BAD,如果AB=6
cm,BD=7
cm,AD=4
cm,那么BC的长为(
B
)
?
?
?
?
A.6
cm
B.4
cm
C.7
cm
D.不能确定
5.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为 3 .?
6.如图,若△OAC≌△OBD,且∠O=68°,∠C=20°,则∠OBD=92°
.?
7.如图所示,在△ABC中,D,E分别是边AC,BC上的点.若△ADB≌△EDB≌△EDC,则∠C的度数为(
D
)
?
?
?
?
A.15°
B.20°
C.25°
D.30°
8.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于下列结论:
①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的个数是(
C
)
A.1
B.2
C.3
D.4
9.如图,∠C=∠CAM=90°,AC=8,BC=4,P,Q两点分别在线段AC和射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则AP的长度为 4或8 .?
10.(滁州期末)如图,已知△ABC≌△DCB,∠ABC=65°,
∠ACB=30°,则∠ACD= 35 °.?
【变式拓展】如图,△ABC≌△ADE,若∠B=80°,∠C=30°,
∠DAC=35°,则∠EAC的度数为(
B
)
?
A.40°
B.35°
C.30°
D.25°
11.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,
∠ACB=20°,则∠ADC的度数是 65° .?
12.一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,3x-2,2y+1.若这两个三角形全等,则x+y的值是
.?
13.如图,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
解:
(1)∵△ABE≌△ACD,∴BE=CD,
∴BE-DE=CD-DE,即BD=CE.
∵BE=6,DE=2,∴CE=BD=BE-DE=4,
∴BC=BE+CE=10.
(2)∵△ABE≌△ACD,∴∠BAE=∠CAD,
∴∠BAD=∠CAE=30°,
∴∠DAE=75°-30°-30°=15°.
14.如图,△ABD≌△EBC,AB=3
cm,BC=4.5
cm,点A,B,C在一条直线上.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
解:(1)∵△ABD≌△EBC,∴AB=EB,BD=BC,
∴DE=BD-BE=4.5-3=1.5(cm).
(2)AC⊥BD.
理由:∵△ABD≌△EBC,∴∠ABD=∠EBC.
又∵∠ABD+∠EBC=180°,
∴∠EBC=90°,∴AC⊥BD.
15.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,
∠EAB=105°,求∠BFD和∠BED的度数.
?
解:∵△ABC≌△ADE,∴∠CAB=∠EAD.
又∵∠CAD=35°,∠EAB=105°,
∠EAD+∠DAC+∠CAB=∠EAB=105°,
∴∠EAD=∠DAC=∠CAB=35°,
∴∠BFD=∠DAB+∠B=70°+20°=90°,
∠BED=∠BFD-∠D=90°-20°=70°.
16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)证明:BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
解:(1)∵△BAD≌△ACE,∴BD=AE,AD=CE,
又∵AE=AD+DE=CE+DE,∴BD=DE+CE.
(2)∵△BAD≌△ACE,∴∠ADB=∠CEA.
∵BD∥CE,∴∠CEA=∠BDE,∴∠ADB=∠BDE.
又∵∠ADB+∠BDE=180°,∴∠ADB=90°,
∴△ABD是∠ADB=90°的直角三角形时,BD∥CE.
