2020秋沪科版八年级数学上册第12章一次函数章末小结与提升课件(共21张PPT)
文档属性
| 名称 | 2020秋沪科版八年级数学上册第12章一次函数章末小结与提升课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
章末小结与提升
第12章 一次函数
函
数
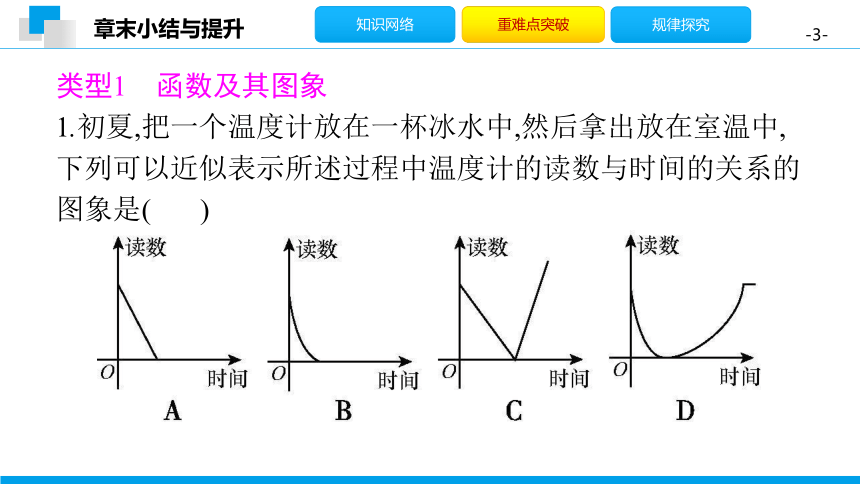
类型1 函数及其图象
1.初夏,把一个温度计放在一杯冰水中,然后拿出放在室温中,下列可以近似表示所述过程中温度计的读数与时间的关系的图象是(
D
)
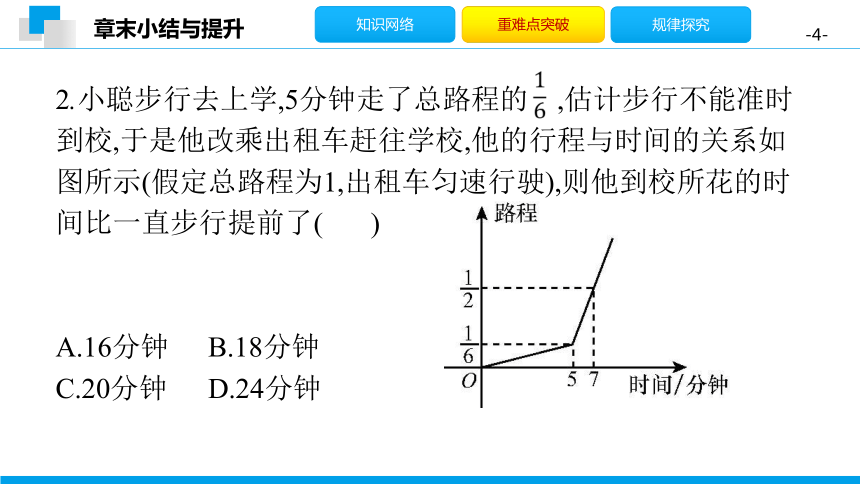
2.小聪步行去上学,5分钟走了总路程的
,估计步行不能准时到校,于是他改乘出租车赶往学校,他的行程与时间的关系如图所示(假定总路程为1,出租车匀速行驶),则他到校所花的时间比一直步行提前了(
C
)
?
A.16分钟
B.18分钟
C.20分钟
D.24分钟
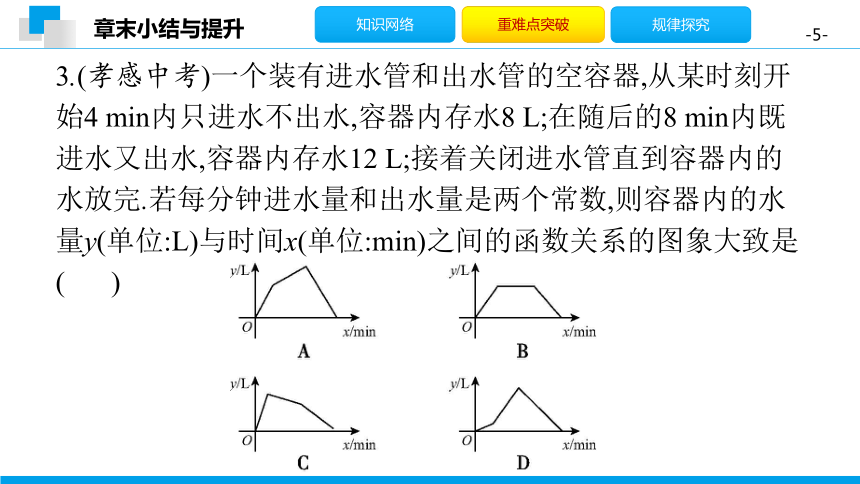
3.(孝感中考)一个装有进水管和出水管的空容器,从某时刻开始4
min内只进水不出水,容器内存水8
L;在随后的8
min内既进水又出水,容器内存水12
L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,则容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致是(
A
)
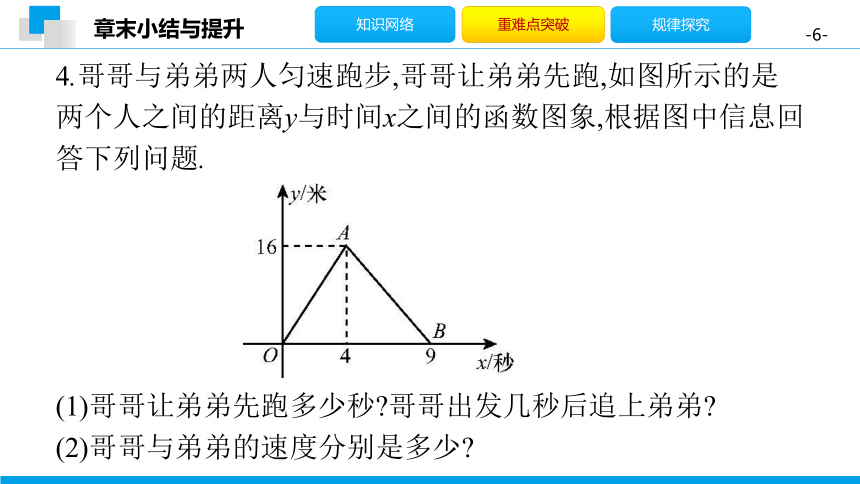
4.哥哥与弟弟两人匀速跑步,哥哥让弟弟先跑,如图所示的是两个人之间的距离y与时间x之间的函数图象,根据图中信息回答下列问题.
(1)哥哥让弟弟先跑多少秒?哥哥出发几秒后追上弟弟?
(2)哥哥与弟弟的速度分别是多少?
解:(1)由图可得,哥哥让弟弟先跑4秒;哥哥出发5秒后追上了弟弟.
(2)由图可得,弟弟先跑4秒的路程为16米,故弟弟的速度为16÷4=4米/秒;
设哥哥的速度为x米/秒,根据哥哥出发后5秒追上弟弟,可得5x-4×5=16,解得x=7.2,故哥哥的速度为7.2米/秒.
类型2 一次函数的图象和性质
5.(沈阳中考)已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是(
B
)
?
A.k<0
B.k<-1
C.k<1
D.k>-1
6.(荆门中考)如果函数y=kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是(
A
)
A.k≥0且b≤0
B.k>0且b≤0
C.k≥0且b<0
D.k>0且b<0
7.(合肥庐阳区期末)关于一次函数y=-3x-2的图象与性质,描述正确的是(
D
)
A.y随x的增大而增大
B.在y轴上的截距为2
C.与x轴交于点(-2,0)
D.函数的图象不经过第一象限
8.已知一次函数y=-0.5x+2,当1≤x≤4时,y的最大值是(
A
)
A.1.5
B.2
C.2.5
D.-6
9.(改编)若一次函数y=mx+|m-1|的图象经过点(0,3),且y随x的增大而增大,则m的值为 4 .?
类型3 一次函数与方程、不等式的关系
10.如图,过点Q(0,3)的一次函数与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是(
D
)
?
A.3x-2y+3=0
B.3x-2y-3=0
C.x-y+3=0
D.x+y-3=0
11.(通辽中考)如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3的解集为(
D
)
?
A.x>-1
B.x<-1
C.x≥3
D.x≥-1
13.(十堰中考)如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式x(kx+b)<0的解集为 -3类型4 一次函数的应用
14.某加工厂有A种原料150千克和充足的B种原料,现准备用这两种原料合成甲、乙两种产品共40件.已知合成甲、乙两种产品需要的A种原料数量及其利润如下表所示:
若设合成的甲种产品有x件(产品件数为整数),这40件产品的总利润为y元,根据以上信息解决下列问题:
(1)求出x的取值范围,并直接写出共有几种合成方案;
(2)写出y关于x的函数关系式,并求出最大利润.
解:(1)根据题意,得3x+5(40-x)≤150,
解得x≥25,所以共有16种合成方案.
(2)根据题意,得y=500x+650(40-x)=-150x+26000,
因为k=-150<0,所以y随x的增大而减小,
所以当x=25时,y有最大值,y最大=-150×25+26000=22250(元).
15.(合肥瑶海区期中)甲、乙两人相约周末登大蜀山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 10 米,乙在A地时距地面的高度b为 30 米;?
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分钟)之间的函数关系式;
(3)登山多长时间时,甲、乙两人的高度差为50米?
解:(2)当0≤x≤2时,y=15x;
当x>2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
所以乙登山全程中,距地面的高度y(米)与登山时间x(分钟)之间的函数关系式为
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分钟)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-(30x-30)=50时,解得x=4;
当30x-30-(10x+100)=50时,解得x=9;
当300-(10x+100)=50时,解得x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人的高度差为50米.
1.(安顺中考)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标为 (2n-1,2n-1) .?
2.(改编)如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2020的长为 22018 .?
章末小结与提升
第12章 一次函数
函
数
类型1 函数及其图象
1.初夏,把一个温度计放在一杯冰水中,然后拿出放在室温中,下列可以近似表示所述过程中温度计的读数与时间的关系的图象是(
D
)
2.小聪步行去上学,5分钟走了总路程的
,估计步行不能准时到校,于是他改乘出租车赶往学校,他的行程与时间的关系如图所示(假定总路程为1,出租车匀速行驶),则他到校所花的时间比一直步行提前了(
C
)
?
A.16分钟
B.18分钟
C.20分钟
D.24分钟
3.(孝感中考)一个装有进水管和出水管的空容器,从某时刻开始4
min内只进水不出水,容器内存水8
L;在随后的8
min内既进水又出水,容器内存水12
L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,则容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致是(
A
)
4.哥哥与弟弟两人匀速跑步,哥哥让弟弟先跑,如图所示的是两个人之间的距离y与时间x之间的函数图象,根据图中信息回答下列问题.
(1)哥哥让弟弟先跑多少秒?哥哥出发几秒后追上弟弟?
(2)哥哥与弟弟的速度分别是多少?
解:(1)由图可得,哥哥让弟弟先跑4秒;哥哥出发5秒后追上了弟弟.
(2)由图可得,弟弟先跑4秒的路程为16米,故弟弟的速度为16÷4=4米/秒;
设哥哥的速度为x米/秒,根据哥哥出发后5秒追上弟弟,可得5x-4×5=16,解得x=7.2,故哥哥的速度为7.2米/秒.
类型2 一次函数的图象和性质
5.(沈阳中考)已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是(
B
)
?
A.k<0
B.k<-1
C.k<1
D.k>-1
6.(荆门中考)如果函数y=kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是(
A
)
A.k≥0且b≤0
B.k>0且b≤0
C.k≥0且b<0
D.k>0且b<0
7.(合肥庐阳区期末)关于一次函数y=-3x-2的图象与性质,描述正确的是(
D
)
A.y随x的增大而增大
B.在y轴上的截距为2
C.与x轴交于点(-2,0)
D.函数的图象不经过第一象限
8.已知一次函数y=-0.5x+2,当1≤x≤4时,y的最大值是(
A
)
A.1.5
B.2
C.2.5
D.-6
9.(改编)若一次函数y=mx+|m-1|的图象经过点(0,3),且y随x的增大而增大,则m的值为 4 .?
类型3 一次函数与方程、不等式的关系
10.如图,过点Q(0,3)的一次函数与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是(
D
)
?
A.3x-2y+3=0
B.3x-2y-3=0
C.x-y+3=0
D.x+y-3=0
11.(通辽中考)如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3的解集为(
D
)
?
A.x>-1
B.x<-1
C.x≥3
D.x≥-1
13.(十堰中考)如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式x(kx+b)<0的解集为 -3
14.某加工厂有A种原料150千克和充足的B种原料,现准备用这两种原料合成甲、乙两种产品共40件.已知合成甲、乙两种产品需要的A种原料数量及其利润如下表所示:
若设合成的甲种产品有x件(产品件数为整数),这40件产品的总利润为y元,根据以上信息解决下列问题:
(1)求出x的取值范围,并直接写出共有几种合成方案;
(2)写出y关于x的函数关系式,并求出最大利润.
解:(1)根据题意,得3x+5(40-x)≤150,
解得x≥25,所以共有16种合成方案.
(2)根据题意,得y=500x+650(40-x)=-150x+26000,
因为k=-150<0,所以y随x的增大而减小,
所以当x=25时,y有最大值,y最大=-150×25+26000=22250(元).
15.(合肥瑶海区期中)甲、乙两人相约周末登大蜀山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 10 米,乙在A地时距地面的高度b为 30 米;?
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分钟)之间的函数关系式;
(3)登山多长时间时,甲、乙两人的高度差为50米?
解:(2)当0≤x≤2时,y=15x;
当x>2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
所以乙登山全程中,距地面的高度y(米)与登山时间x(分钟)之间的函数关系式为
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分钟)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-(30x-30)=50时,解得x=4;
当30x-30-(10x+100)=50时,解得x=9;
当300-(10x+100)=50时,解得x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人的高度差为50米.
1.(安顺中考)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标为 (2n-1,2n-1) .?
2.(改编)如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2020的长为 22018 .?
