2020秋沪科版八年级数学上册第14章全等三角形章末小结与提升课件(共17张PPT)
文档属性
| 名称 | 2020秋沪科版八年级数学上册第14章全等三角形章末小结与提升课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 17:33:43 | ||
图片预览


文档简介
(共17张PPT)
章末小结与提升
第14章 全等三角形
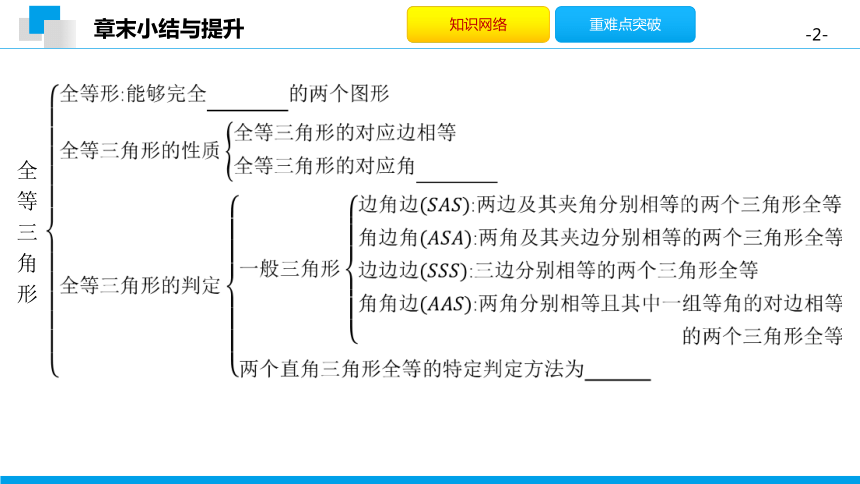
全
等
三
角
形
类型1 全等三角形的性质
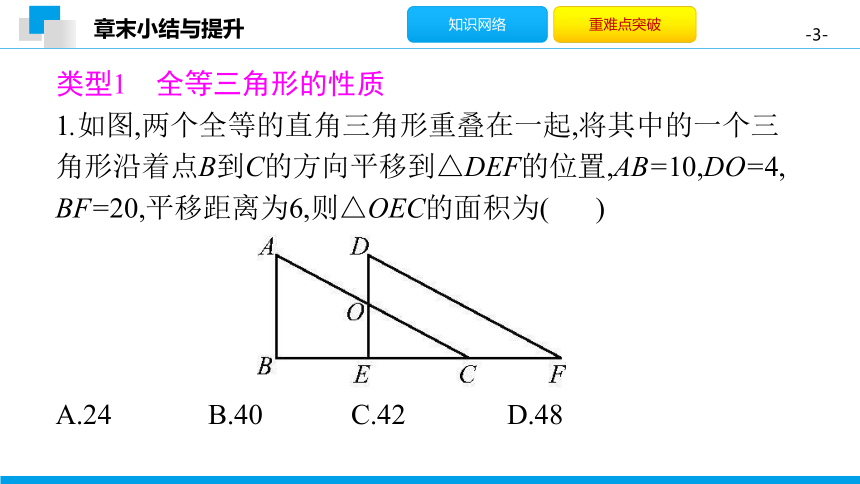
1.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,
BF=20,平移距离为6,则△OEC的面积为(
A
)
A.24
B.40
C.42
D.48
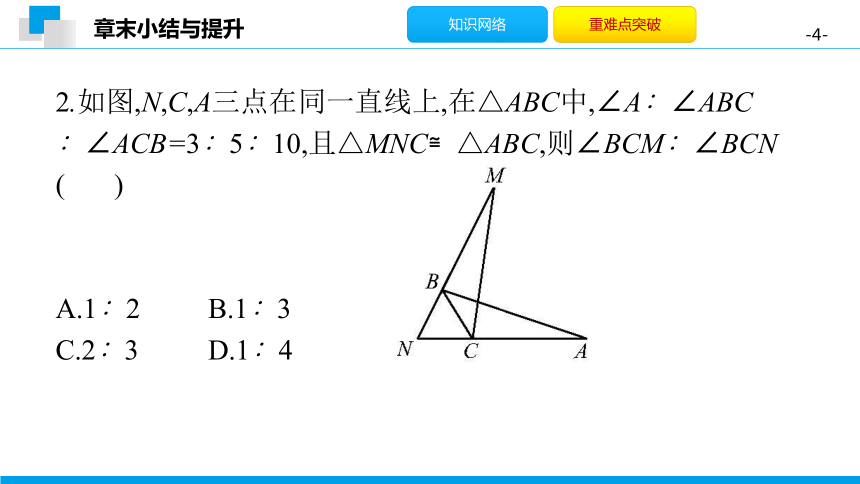
2.如图,N,C,A三点在同一直线上,在△ABC中,∠A∶∠ABC
∶∠ACB=3∶5∶10,且△MNC≌△ABC,则∠BCM∶∠BCN
(
D
)
A.1∶2
B.1∶3
C.2∶3
D.1∶4
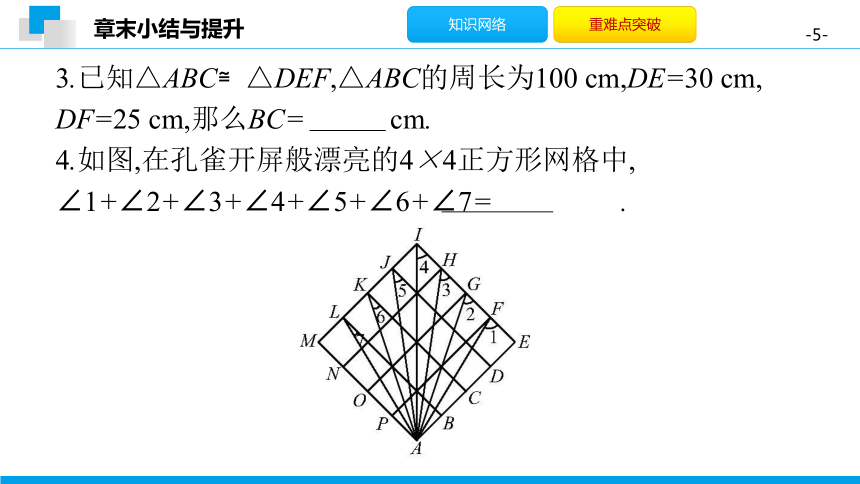
3.已知△ABC≌△DEF,△ABC的周长为100
cm,DE=30
cm,
DF=25
cm,那么BC= 45 cm.?
4.如图,在孔雀开屏般漂亮的4×4正方形网格中,
∠1+∠2+∠3+∠4+∠5+∠6+∠7= 315° .?
类型2 全等三角形的判定
5.(滁州期末)根据下列已知条件,能画出唯一△ABC的是(
C
)
A.AB=3,BC=4,AC=8
B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4
D.∠C=90°,AB=4
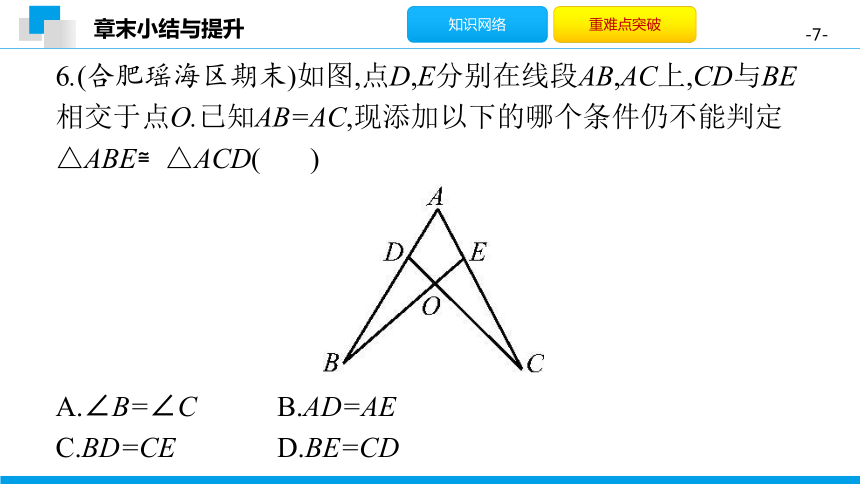
6.(合肥瑶海区期末)如图,点D,E分别在线段AB,AC上,CD与BE相交于点O.已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD(
D
)
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD
7.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S.若AQ=PQ,PR=PS,则下列结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④BR=QS.其中一定正确的结论是
①② .(填写序号)?
8.如图,已知在△ABC和△A'B'C'中,AD,A'D'分别是△ABC和△A'B'C'的中线,AB=A'B',BC=B'C',AD=A'D'.求证:
△ABC≌△A'B'C'.
证明:∵AD,A'D'分别是△ABC和△A'B'C'的中线,BC=B'C',
∴BD=B'D'.
又∵AB=A'B',AD=A'D',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'.
又∵AB=A'B',BC=B'C',
∴△ABC≌△A'B'C'(SAS).
类型3 全等三角形的性质与判定的综合应用
9.如图,AC∥BD,AB∥CD,AD与BC交于点O,AE⊥BC于点E,
DF⊥BC于点F,那么图中全等的三角形共(
C
)
?
A.5对
B.6对
C.7对
D.8对
10.如图,C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是 ①②③ .(填出所有正确结论的序号)?
11.在Rt△ABC中,BC=AC,∠ACB=90°,D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE,BF.
(1)当点D在线段AB上时(点D不与点A,B重合),如图1,线段BF,AD所在直线的位置关系为 垂直 ,线段BF,AD的数量关系为 相等 .?
(2)当点D在线段AB的延长线上时,如图2,则(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,请说明理由.
解:成立.理由如下:
∵CD⊥EF,∴∠DCF=90°.
∵∠ACB=90°,∴∠DCF+∠BCD=∠ACB+∠BCD,
即∠ACD=∠BCF.
∵BC=AC,CD=CF,∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
类型4 全等三角形的实际应用
12.如图所示,A,B在一个水池的两侧,若BE=DE,
∠B=∠D=90°,CD=8
m,则水池宽AB= 8 m.?
13.如图,某铁路施工队在建设铁路的过程中,需要打通一座小山,设计时要测量隧道的长度,小山前面恰好是一块空地,利用这一有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道长度?说明理由.
解:可以.答案不唯一,合理即可.
①如图,找个能同时看见A点和B点的C点,然后连接AC并延长至点D,使DC=AC;
?
②连接BC并延长至点E,使EC=BC,测量DE的长度,即为AB的距离.
理由:∵AC=DC,∠ACB=∠DCE,BC=EC,
∴△ACB≌△DCE(SAS),∴AB=DE.
章末小结与提升
第14章 全等三角形
全
等
三
角
形
类型1 全等三角形的性质
1.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,
BF=20,平移距离为6,则△OEC的面积为(
A
)
A.24
B.40
C.42
D.48
2.如图,N,C,A三点在同一直线上,在△ABC中,∠A∶∠ABC
∶∠ACB=3∶5∶10,且△MNC≌△ABC,则∠BCM∶∠BCN
(
D
)
A.1∶2
B.1∶3
C.2∶3
D.1∶4
3.已知△ABC≌△DEF,△ABC的周长为100
cm,DE=30
cm,
DF=25
cm,那么BC= 45 cm.?
4.如图,在孔雀开屏般漂亮的4×4正方形网格中,
∠1+∠2+∠3+∠4+∠5+∠6+∠7= 315° .?
类型2 全等三角形的判定
5.(滁州期末)根据下列已知条件,能画出唯一△ABC的是(
C
)
A.AB=3,BC=4,AC=8
B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4
D.∠C=90°,AB=4
6.(合肥瑶海区期末)如图,点D,E分别在线段AB,AC上,CD与BE相交于点O.已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD(
D
)
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD
7.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S.若AQ=PQ,PR=PS,则下列结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④BR=QS.其中一定正确的结论是
①② .(填写序号)?
8.如图,已知在△ABC和△A'B'C'中,AD,A'D'分别是△ABC和△A'B'C'的中线,AB=A'B',BC=B'C',AD=A'D'.求证:
△ABC≌△A'B'C'.
证明:∵AD,A'D'分别是△ABC和△A'B'C'的中线,BC=B'C',
∴BD=B'D'.
又∵AB=A'B',AD=A'D',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'.
又∵AB=A'B',BC=B'C',
∴△ABC≌△A'B'C'(SAS).
类型3 全等三角形的性质与判定的综合应用
9.如图,AC∥BD,AB∥CD,AD与BC交于点O,AE⊥BC于点E,
DF⊥BC于点F,那么图中全等的三角形共(
C
)
?
A.5对
B.6对
C.7对
D.8对
10.如图,C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是 ①②③ .(填出所有正确结论的序号)?
11.在Rt△ABC中,BC=AC,∠ACB=90°,D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE,BF.
(1)当点D在线段AB上时(点D不与点A,B重合),如图1,线段BF,AD所在直线的位置关系为 垂直 ,线段BF,AD的数量关系为 相等 .?
(2)当点D在线段AB的延长线上时,如图2,则(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,请说明理由.
解:成立.理由如下:
∵CD⊥EF,∴∠DCF=90°.
∵∠ACB=90°,∴∠DCF+∠BCD=∠ACB+∠BCD,
即∠ACD=∠BCF.
∵BC=AC,CD=CF,∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
类型4 全等三角形的实际应用
12.如图所示,A,B在一个水池的两侧,若BE=DE,
∠B=∠D=90°,CD=8
m,则水池宽AB= 8 m.?
13.如图,某铁路施工队在建设铁路的过程中,需要打通一座小山,设计时要测量隧道的长度,小山前面恰好是一块空地,利用这一有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道长度?说明理由.
解:可以.答案不唯一,合理即可.
①如图,找个能同时看见A点和B点的C点,然后连接AC并延长至点D,使DC=AC;
?
②连接BC并延长至点E,使EC=BC,测量DE的长度,即为AB的距离.
理由:∵AC=DC,∠ACB=∠DCE,BC=EC,
∴△ACB≌△DCE(SAS),∴AB=DE.
