2020秋沪科版八年级数学上册第15章轴对称图形与等腰三角形章末小结与提升课件(共28张PPT)
文档属性
| 名称 | 2020秋沪科版八年级数学上册第15章轴对称图形与等腰三角形章末小结与提升课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 431.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 17:34:50 | ||
图片预览




文档简介
(共28张PPT)
章末小结与提升
第15章 轴对称图形与等腰三角形
轴
对
称
类型1 轴对称与轴对称图形
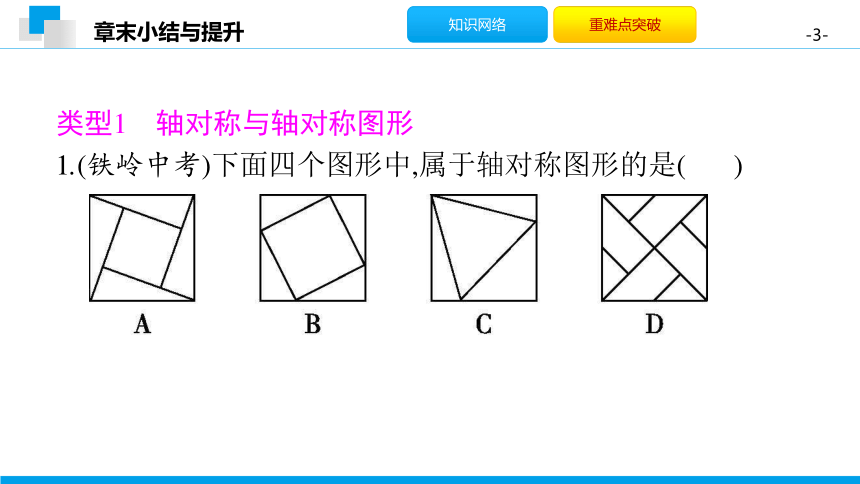
1.(铁岭中考)下面四个图形中,属于轴对称图形的是(
C
)
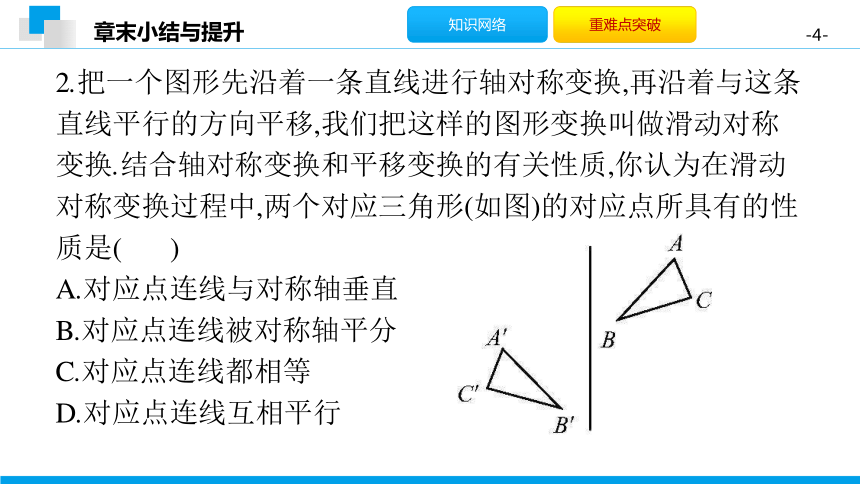
2.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图)的对应点所具有的性质是(
B
)
A.对应点连线与对称轴垂直
B.对应点连线被对称轴平分
C.对应点连线都相等
D.对应点连线互相平行
3.已知△ABC的周长为l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是(
C
)
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
类型2 线段的垂直平分线
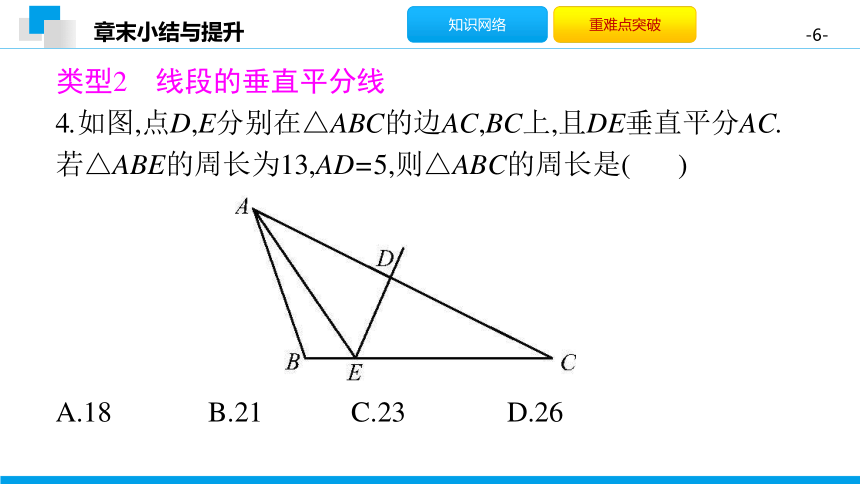
4.如图,点D,E分别在△ABC的边AC,BC上,且DE垂直平分AC.若△ABE的周长为13,AD=5,则△ABC的周长是(
C
)
?
A.18
B.21
C.23
D.26
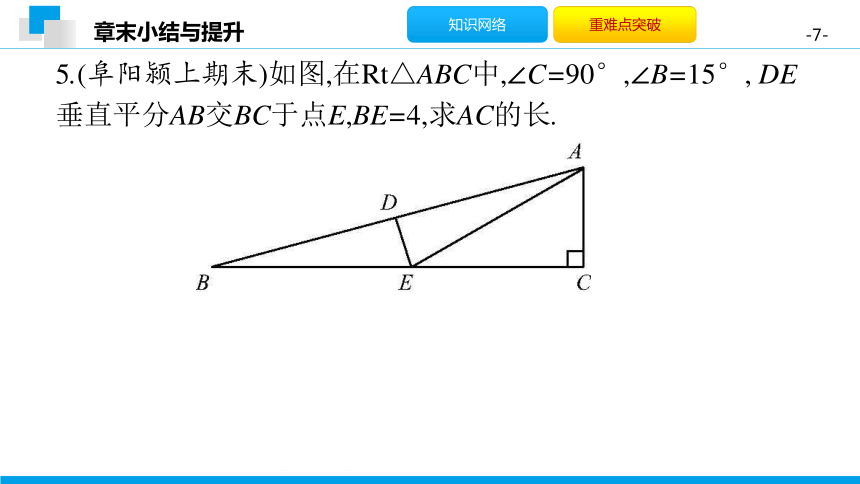
5.(阜阳颍上期末)如图,在Rt△ABC中,∠C=90°,∠B=15°,
DE垂直平分AB交BC于点E,BE=4,求AC的长.
解:∵DE垂直平分AB,∴AE=BE=4,
∴∠BAE=∠B=15°,
∴∠AEC=∠BAE+∠B=30°.
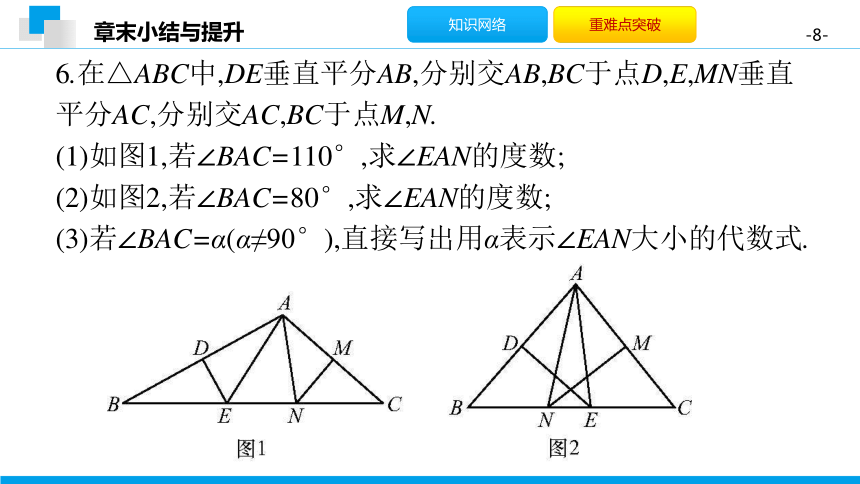
6.在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图1,若∠BAC=110°,求∠EAN的度数;
(2)如图2,若∠BAC=80°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C)
=110°-70°=40°.
(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=∠B+∠C-∠BAC
=100°-80°=20°.
(3)当0°<α<90°时,∠EAN=180°-2α;
当90°<α<180°时,∠EAN=2α-180°.
类型3 等腰三角形的性质与判定
7.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,
∠A=∠ABD.若AC=5,BC=3,则2BD的长是(
A
)
8.如图,在△ABC中,BF,CF是角平分线,DE∥BC,分别交AB,AC于点D,E,DE经过点F.则下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长=AB+AC;④BF=CF.其中正确的结论有(
C
)
?
?
A.1个
B.2个
C.3个
D.4个
9.(合肥包河区期末)若等腰三角形一腰上的高与另一腰的夹角为20°,则这个等腰三角形的底角为 55°或35° .?
10.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.
(1)求证:EF⊥AB;
(2)求证:△ACF为等腰三角形.
证明:(1)∵AB=AC,∠BAC=36°,∴∠ABC=72°.
又∵BD是∠ABC的平分线,∴∠ABD=36°,
∴∠BAD=∠ABD,∴AD=BD.
又∵E是AB的中点,∴DE⊥AB,即EF⊥AB.
(2)∵EF⊥AB,AE=BE,∴EF垂直平分AB,
∴AF=BF,∴∠BAF=∠ABF.
∵∠ABD=∠BAD,∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,∴∠AFC=∠ACB-∠CAF=36°,
∴∠CAF=∠AFC=36°,∴AC=CF,
∴△ACF为等腰三角形.
11.(1)如图1,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE.已知∠EDM=84°,求∠A的度数;
(2)如图2,点B,F,D在射线AM上,点G,C,E在射线AN上,且AB=BC=CD=DE=EF=FG=GA,求∠A的度数.
解:(1)∵AB=BC=CD=DE,
∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED.
根据三角形的外角性质,得∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,
∠A+∠CED=∠EDM.
又∵∠EDM=84°,∴∠A+3∠A=84°,
解得∠A=21°.
(2)设∠A=x°,∵AB=BC=CD=DE=EF=FG=GA,
∴∠AFG=∠ACB=x°,
∠CGF=∠CEF=∠CBF=∠CDF=2x°,
∠ECD=∠CED=∠EFD=∠EDF=3x°,
又∵∠A+∠CED+∠EDF=180°,
即x+3x+3x=180,
类型4 含30°角的直角三角形的性质
12.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若AD=6,则CD等于(
A
)
?
A.3
B.4
C.5
D.6
13.等腰三角形一腰上的高与腰长之比为1∶2,则等腰三角形顶角的度数为(
C
)
A.30°
B.60°或120°
C.30°或150°
D.150°
14.(淮南田家庵区期中)若直角三角形的一个锐角为30°,而斜边与较短边之和为24,那么斜边的长为 16 .?
15.如图,在△ABC中,∠C=90°,∠A=60°,BC=6,点D在射线BC上,∠ADC=60°,则点D到斜边AB的距离等于 2或4 .?
16.如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向.轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
(1)求此时轮船距小岛多少海里?
(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
解:(1)∵∠PAB=15°,∠PBC=30°,
∴∠PAB=∠APB,
∴PB=AB=15×3=45(海里).
(2)过点P作PD⊥BC于点D.
在Rt△PBD中,∠PBD=30°,PB=45,
∴PD=
PB=22.5,
∵22.5>20,
∴轮船继续向前航行,不会有触礁危险.
17.如图,在等边△ABC中,AB=2,P是AB边上任意一点(点P可以与点A重合),过点P作PE⊥BC,垂足为E,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q.求当BP的长等于多少时,点P与点Q重合?
类型5 角的平分线
18.如图,A,B分别是∠NOP,∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则以下结论错误的是
(
C
)
A.AD+BC=AB
B.∠AOB=90°
C.与∠CBO互余的角有2个
D.点O是CD的中点
19.如图,在△ABC中,AB=8,BC=10,BD是△ABC的角平分线,
DE⊥AB于点E.若DE=4,则△ABC的面积为 36 .?
20.如图,在△ABC中,∠ABC=120°,∠C=26°,且DE⊥AB,
DF⊥AC,DE=DF.求∠ADC的度数.
解:∵∠ABC=120°,∠C=26°,
∴∠BAC=180°-120°-26°=34°.
∵DE⊥AB,DF⊥AC,DE=DF,
∴点D在∠BAC的平分线上,
∴在△ADC中,
∠ADC=180°-∠DAF-∠C=180°-17°-26°=137°.
章末小结与提升
第15章 轴对称图形与等腰三角形
轴
对
称
类型1 轴对称与轴对称图形
1.(铁岭中考)下面四个图形中,属于轴对称图形的是(
C
)
2.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图)的对应点所具有的性质是(
B
)
A.对应点连线与对称轴垂直
B.对应点连线被对称轴平分
C.对应点连线都相等
D.对应点连线互相平行
3.已知△ABC的周长为l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是(
C
)
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
类型2 线段的垂直平分线
4.如图,点D,E分别在△ABC的边AC,BC上,且DE垂直平分AC.若△ABE的周长为13,AD=5,则△ABC的周长是(
C
)
?
A.18
B.21
C.23
D.26
5.(阜阳颍上期末)如图,在Rt△ABC中,∠C=90°,∠B=15°,
DE垂直平分AB交BC于点E,BE=4,求AC的长.
解:∵DE垂直平分AB,∴AE=BE=4,
∴∠BAE=∠B=15°,
∴∠AEC=∠BAE+∠B=30°.
6.在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图1,若∠BAC=110°,求∠EAN的度数;
(2)如图2,若∠BAC=80°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C)
=110°-70°=40°.
(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=∠B+∠C-∠BAC
=100°-80°=20°.
(3)当0°<α<90°时,∠EAN=180°-2α;
当90°<α<180°时,∠EAN=2α-180°.
类型3 等腰三角形的性质与判定
7.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,
∠A=∠ABD.若AC=5,BC=3,则2BD的长是(
A
)
8.如图,在△ABC中,BF,CF是角平分线,DE∥BC,分别交AB,AC于点D,E,DE经过点F.则下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长=AB+AC;④BF=CF.其中正确的结论有(
C
)
?
?
A.1个
B.2个
C.3个
D.4个
9.(合肥包河区期末)若等腰三角形一腰上的高与另一腰的夹角为20°,则这个等腰三角形的底角为 55°或35° .?
10.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.
(1)求证:EF⊥AB;
(2)求证:△ACF为等腰三角形.
证明:(1)∵AB=AC,∠BAC=36°,∴∠ABC=72°.
又∵BD是∠ABC的平分线,∴∠ABD=36°,
∴∠BAD=∠ABD,∴AD=BD.
又∵E是AB的中点,∴DE⊥AB,即EF⊥AB.
(2)∵EF⊥AB,AE=BE,∴EF垂直平分AB,
∴AF=BF,∴∠BAF=∠ABF.
∵∠ABD=∠BAD,∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,∴∠AFC=∠ACB-∠CAF=36°,
∴∠CAF=∠AFC=36°,∴AC=CF,
∴△ACF为等腰三角形.
11.(1)如图1,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE.已知∠EDM=84°,求∠A的度数;
(2)如图2,点B,F,D在射线AM上,点G,C,E在射线AN上,且AB=BC=CD=DE=EF=FG=GA,求∠A的度数.
解:(1)∵AB=BC=CD=DE,
∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED.
根据三角形的外角性质,得∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,
∠A+∠CED=∠EDM.
又∵∠EDM=84°,∴∠A+3∠A=84°,
解得∠A=21°.
(2)设∠A=x°,∵AB=BC=CD=DE=EF=FG=GA,
∴∠AFG=∠ACB=x°,
∠CGF=∠CEF=∠CBF=∠CDF=2x°,
∠ECD=∠CED=∠EFD=∠EDF=3x°,
又∵∠A+∠CED+∠EDF=180°,
即x+3x+3x=180,
类型4 含30°角的直角三角形的性质
12.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若AD=6,则CD等于(
A
)
?
A.3
B.4
C.5
D.6
13.等腰三角形一腰上的高与腰长之比为1∶2,则等腰三角形顶角的度数为(
C
)
A.30°
B.60°或120°
C.30°或150°
D.150°
14.(淮南田家庵区期中)若直角三角形的一个锐角为30°,而斜边与较短边之和为24,那么斜边的长为 16 .?
15.如图,在△ABC中,∠C=90°,∠A=60°,BC=6,点D在射线BC上,∠ADC=60°,则点D到斜边AB的距离等于 2或4 .?
16.如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向.轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
(1)求此时轮船距小岛多少海里?
(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
解:(1)∵∠PAB=15°,∠PBC=30°,
∴∠PAB=∠APB,
∴PB=AB=15×3=45(海里).
(2)过点P作PD⊥BC于点D.
在Rt△PBD中,∠PBD=30°,PB=45,
∴PD=
PB=22.5,
∵22.5>20,
∴轮船继续向前航行,不会有触礁危险.
17.如图,在等边△ABC中,AB=2,P是AB边上任意一点(点P可以与点A重合),过点P作PE⊥BC,垂足为E,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q.求当BP的长等于多少时,点P与点Q重合?
类型5 角的平分线
18.如图,A,B分别是∠NOP,∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则以下结论错误的是
(
C
)
A.AD+BC=AB
B.∠AOB=90°
C.与∠CBO互余的角有2个
D.点O是CD的中点
19.如图,在△ABC中,AB=8,BC=10,BD是△ABC的角平分线,
DE⊥AB于点E.若DE=4,则△ABC的面积为 36 .?
20.如图,在△ABC中,∠ABC=120°,∠C=26°,且DE⊥AB,
DF⊥AC,DE=DF.求∠ADC的度数.
解:∵∠ABC=120°,∠C=26°,
∴∠BAC=180°-120°-26°=34°.
∵DE⊥AB,DF⊥AC,DE=DF,
∴点D在∠BAC的平分线上,
∴在△ADC中,
∠ADC=180°-∠DAF-∠C=180°-17°-26°=137°.
