2020秋沪科版八年级数学上册11.2图形在坐标系中的平移习题课件(共17张PPT)
文档属性
| 名称 | 2020秋沪科版八年级数学上册11.2图形在坐标系中的平移习题课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 18:11:46 | ||
图片预览





文档简介
(共17张PPT)
11.2 图形在坐标系中的平移
第11章 平面直角坐标系
知识点1 点在坐标系中的平移
1.将点(-5,3)沿x轴的正方向平移3个单位后的坐标是(
C
)
A.(8,3)
B.(-8,3)
C.(-2,3)
D.(-5,0)
2.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是
(2,-1) .?
知识点2 图形在坐标系中的平移
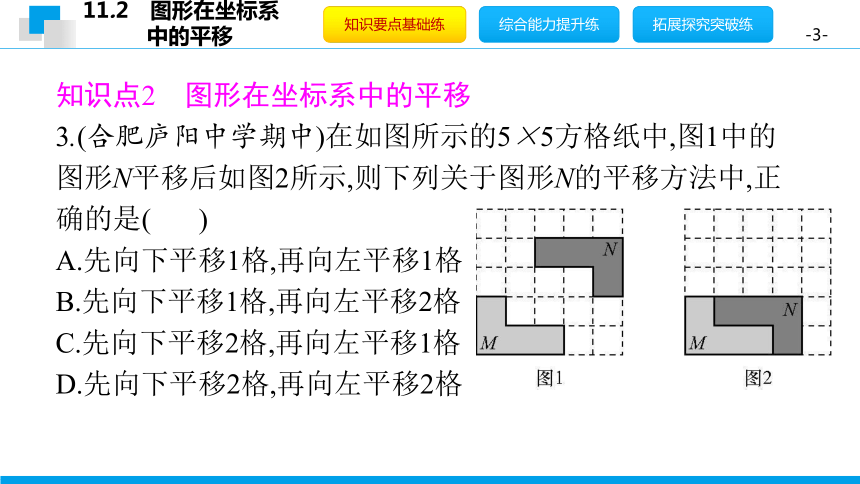
3.(合肥庐阳中学期中)在如图所示的5×5方格纸中,图1中的图形N平移后如图2所示,则下列关于图形N的平移方法中,正确的是(
C
)?
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
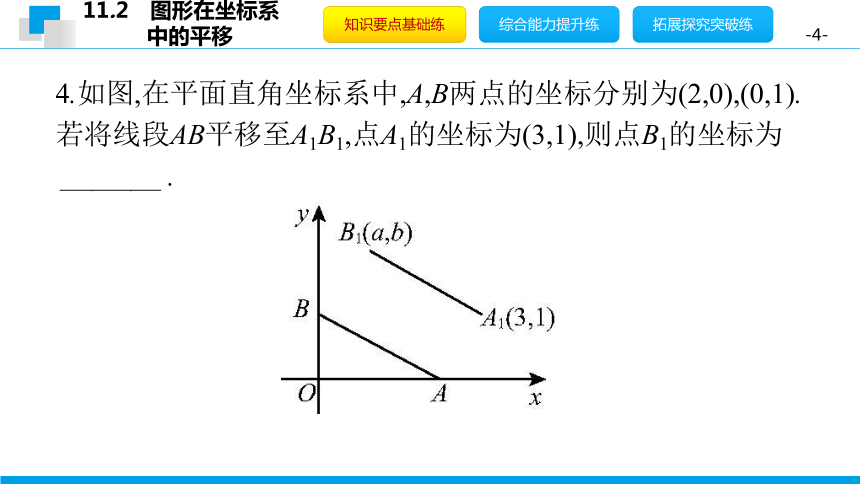
4.如图,在平面直角坐标系中,A,B两点的坐标分别为(2,0),(0,1).若将线段AB平移至A1B1,点A1的坐标为(3,1),则点B1的坐标为
(1,2) .?
知识点3 图形的平移与坐标变化的互逆关系
5.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则线段AB可以通过以下哪种方式平移得到线段CD
(
C
)
A.先向上平移3个单位,再向左平移5个单位
B.先向左平移5个单位,再向下平移3个单位
C.先向上平移3个单位,再向右平移5个单位
D.先向右平移5个单位,再向下平移3个单位
6.(教材P14练习第3题变式)在平面直角坐标系中,若点P(x-3,
y+1)平移后得到点P1(x,y),则点Q(5,3)作同样的平移后的坐标为 (8,2) .?
7.在平面直角坐标系中,将点P(1,-2)向右平移3个单位,再向上平移4个单位,得到的点P1的坐标为(
B
)
A.(-2,2)
B.(4,2)
C.(5,1)
D.(5,-5)
【变式拓展】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(
D
)
A.(2,5)
B.(-8,5)
C.(-8,-1)
D.(2,-1)
8.(合肥蜀山区期末)在第四象限内有一点A到x轴的距离是2,到y轴的距离是3,则点A向左平移1个单位长度后的坐标是
(
C
)
A.(1,-3)
B.(-1,3)
C.(2,-2)
D.(4,-2)
9.将点P(-3,y)先向下平移3个单位长度,再向左平移2个单位长度后得到点Q(x,-1),则xy= -10 .?
10.已知坐标平面内点A(-2,5),如果将坐标轴先向左平移3个单位,再向上平移4个单位,那么点A在新坐标系中的坐标为
(1,1) .
11.(改编)如图,将边长为6的等边△ABC沿BC方向平移3个单位得到△DEF,则四边形ABFD的周长为 24 .?
12.如图,在正方形网格中有点A(3,-1).
(1)将点A向左平移4个单位,得到点A1,请在图上标出这个点,并写出它的坐标;
(2)将点A向上平移4个单位,得到点A2,请在图上标出这个点,并写出它的坐标;
(3)你能判断直线AA1与x轴、直线AA2与y轴的位置关系吗?
解:(1)图略,A1(-1,-1).
(2)图略,A2(3,3).
(3)AA1∥x轴,AA2∥y轴.
13.已知△ABC的三个顶点坐标分别为A(0,0),B(3,0),C(2,3).
(1)把△ABC向右平移3个单位,再向下平移2个单位,得到△A'B'C',写出点A',B',C'的坐标.
(2)若△A″B″C″三个顶点的坐标分别是A″(-2,-3),B″(1,-3),
C″(0,0),则△A″B″C″是由△ABC经过怎样的平移得到的?
解:(1)A'(3,-2),B'(6,-2),C'(5,1).
(2)将△ABC先向左平移2个单位,再向下平移3个单位,得到△A″B″C″.
14.如图,有8×8的正方形网格,每个小正方形的边长为1个单位长度.按要求操作并计算.
(1)在8×8的正方形网格中建立平面直角坐标系,使点A的坐标为(2,4),点B的坐标为(4,2);
(2)将点A向下平移5个单位,再关于y轴对称得到点C,求点C的坐标;
(3)画出△ABC,并求其面积.
解:(1)图略.
(2)图略,点C的坐标为(-2,-1).
15.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点
,B为y轴上的一个动点.
(1)若已知点B(0,2),则点A与点B的“非常距离”为 2 ;?
(2)若点A与点B的“非常距离”为3,则点B的坐标为(0,3)或(0,-3);
(3)点A与点B的“非常距离”的最小值为? .?
11.2 图形在坐标系中的平移
第11章 平面直角坐标系
知识点1 点在坐标系中的平移
1.将点(-5,3)沿x轴的正方向平移3个单位后的坐标是(
C
)
A.(8,3)
B.(-8,3)
C.(-2,3)
D.(-5,0)
2.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是
(2,-1) .?
知识点2 图形在坐标系中的平移
3.(合肥庐阳中学期中)在如图所示的5×5方格纸中,图1中的图形N平移后如图2所示,则下列关于图形N的平移方法中,正确的是(
C
)?
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
4.如图,在平面直角坐标系中,A,B两点的坐标分别为(2,0),(0,1).若将线段AB平移至A1B1,点A1的坐标为(3,1),则点B1的坐标为
(1,2) .?
知识点3 图形的平移与坐标变化的互逆关系
5.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则线段AB可以通过以下哪种方式平移得到线段CD
(
C
)
A.先向上平移3个单位,再向左平移5个单位
B.先向左平移5个单位,再向下平移3个单位
C.先向上平移3个单位,再向右平移5个单位
D.先向右平移5个单位,再向下平移3个单位
6.(教材P14练习第3题变式)在平面直角坐标系中,若点P(x-3,
y+1)平移后得到点P1(x,y),则点Q(5,3)作同样的平移后的坐标为 (8,2) .?
7.在平面直角坐标系中,将点P(1,-2)向右平移3个单位,再向上平移4个单位,得到的点P1的坐标为(
B
)
A.(-2,2)
B.(4,2)
C.(5,1)
D.(5,-5)
【变式拓展】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(
D
)
A.(2,5)
B.(-8,5)
C.(-8,-1)
D.(2,-1)
8.(合肥蜀山区期末)在第四象限内有一点A到x轴的距离是2,到y轴的距离是3,则点A向左平移1个单位长度后的坐标是
(
C
)
A.(1,-3)
B.(-1,3)
C.(2,-2)
D.(4,-2)
9.将点P(-3,y)先向下平移3个单位长度,再向左平移2个单位长度后得到点Q(x,-1),则xy= -10 .?
10.已知坐标平面内点A(-2,5),如果将坐标轴先向左平移3个单位,再向上平移4个单位,那么点A在新坐标系中的坐标为
(1,1) .
11.(改编)如图,将边长为6的等边△ABC沿BC方向平移3个单位得到△DEF,则四边形ABFD的周长为 24 .?
12.如图,在正方形网格中有点A(3,-1).
(1)将点A向左平移4个单位,得到点A1,请在图上标出这个点,并写出它的坐标;
(2)将点A向上平移4个单位,得到点A2,请在图上标出这个点,并写出它的坐标;
(3)你能判断直线AA1与x轴、直线AA2与y轴的位置关系吗?
解:(1)图略,A1(-1,-1).
(2)图略,A2(3,3).
(3)AA1∥x轴,AA2∥y轴.
13.已知△ABC的三个顶点坐标分别为A(0,0),B(3,0),C(2,3).
(1)把△ABC向右平移3个单位,再向下平移2个单位,得到△A'B'C',写出点A',B',C'的坐标.
(2)若△A″B″C″三个顶点的坐标分别是A″(-2,-3),B″(1,-3),
C″(0,0),则△A″B″C″是由△ABC经过怎样的平移得到的?
解:(1)A'(3,-2),B'(6,-2),C'(5,1).
(2)将△ABC先向左平移2个单位,再向下平移3个单位,得到△A″B″C″.
14.如图,有8×8的正方形网格,每个小正方形的边长为1个单位长度.按要求操作并计算.
(1)在8×8的正方形网格中建立平面直角坐标系,使点A的坐标为(2,4),点B的坐标为(4,2);
(2)将点A向下平移5个单位,再关于y轴对称得到点C,求点C的坐标;
(3)画出△ABC,并求其面积.
解:(1)图略.
(2)图略,点C的坐标为(-2,-1).
15.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点
,B为y轴上的一个动点.
(1)若已知点B(0,2),则点A与点B的“非常距离”为 2 ;?
(2)若点A与点B的“非常距离”为3,则点B的坐标为(0,3)或(0,-3);
(3)点A与点B的“非常距离”的最小值为? .?
