人教版八年级数学上册12.1全等三角形导学案
文档属性
| 名称 | 人教版八年级数学上册12.1全等三角形导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 149.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册第十二章12.1 全等三角形
导学案
教学目标
1.知道什么是全等形、全等三角形及全等三角形的对应元素.
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等.
3.能熟练找出两个全等三角形的对应角、对应边.
预习反馈
阅读教材P31~32,完成下列内容.
1.全等形、全等三角形的概念:能够完全重合的两个图形叫做全等形;能够完全重合的两个三角形叫做全等三角形.如下列图形中的全等形是e与h、d与g.
2.把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
如图,△ABC与△DEF能重合,则记作:△ABC≌△DEF,对应顶点:点A与点D、点B与点E、点C与点F;对应边:AB与DE、AC与DF、BC与EF;对应角:∠A与∠D、∠B与∠E、∠C与∠F.
3.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.
如上图,△ABC≌△DEF,则AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F.
例题讲解
类型1 全等形的识别
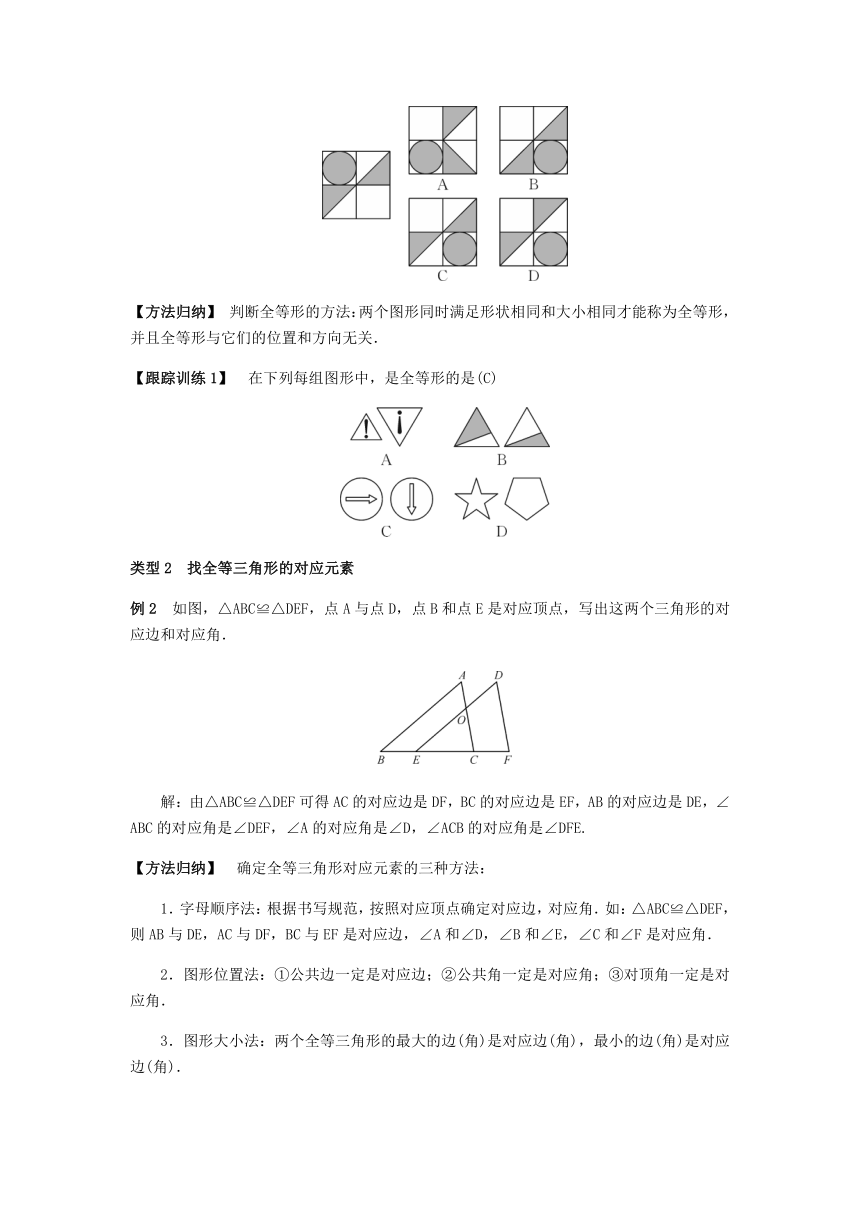
例1 如图,在4个正方形图案中,与如图所示正方形图案全等的图案是(C)
【方法归纳】 判断全等形的方法:两个图形同时满足形状相同和大小相同才能称为全等形,并且全等形与它们的位置和方向无关.
【跟踪训练1】 在下列每组图形中,是全等形的是(C)
类型2 找全等三角形的对应元素
例2 如图,△ABC≌△DEF,点A与点D,点B和点E是对应顶点,写出这两个三角形的对应边和对应角.
解:由△ABC≌△DEF可得AC的对应边是DF,BC的对应边是EF,AB的对应边是DE,∠ABC的对应角是∠DEF,∠A的对应角是∠D,∠ACB的对应角是∠DFE.
【方法归纳】 确定全等三角形对应元素的三种方法:
1.字母顺序法:根据书写规范,按照对应顶点确定对应边,对应角.如:△ABC≌△DEF,则AB与DE,AC与DF,BC与EF是对应边,∠A和∠D,∠B和∠E,∠C和∠F是对应角.
2.图形位置法:①公共边一定是对应边;②公共角一定是对应角;③对顶角一定是对应角.
3.图形大小法:两个全等三角形的最大的边(角)是对应边(角),最小的边(角)是对应边(角).
【跟踪训练2】 如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
解:对应边:AN与AM,BN与CM;
对应角:∠BAN与∠CAM,∠ANB与∠AMC.
类型3 运用全等三角形的性质解决问题
例3 如图所示,△ABC绕着点B顺时针旋转90°得到△DBE,且∠ABC=90°.
(1)△ABC和△DBE是否全等?若全等,指出对应边和对应角;
(2)直线CD,DE有怎样的位置关系?
解:(1)∵△ABC绕着点B沿顺时针方向旋转90°得到△DBE,
∴△ABC≌△DBE.
∴∠BAC的对应角为∠BDE,∠ACB的对应角为∠DEB,∠ABC的对应角为∠DBE;AB的对应边为DB,BC的对应边为BE,AC的对应边为DE.
(2)AC⊥DE.
理由:延长AC,交DE于点F.
∵∠ABC=90°,∴∠A+∠1=90°.
又∵△ABC≌△DBE,∴∠D=∠A.
又∵∠2=∠1,∴∠2+∠D=90°.
∴AC⊥DE.
【方法归纳】 全等三角形的性质的用途
【跟踪训练3】 如图,把△ABC沿直线BA翻折至△ABD,那么△ABC和△ABD是全等图形(填“是”或“不是”).若CB=5,则DB=5;若△ABC的面积为10,则△ABD的面积为10.
巩固训练
1.下列关于全等三角形的说法,不正确的是(A)
A.形状相同的三角形是全等三角形
B.全等三角形的形状相同
C.全等三角形的大小相等
D.全等三角形的对应边相等
2.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是(C)
A.AC=CE
B.∠BAC=∠ECD
C.∠ACB=∠ECD
D.∠B=∠D
3.如图,若△OAD≌△OBC,∠COD=65°,∠C=20°,则∠OAD的度数为(D)
A.65°
B.75°
C.85°
D.95°
4.已知△ABC≌△A′B′C′,点A与A′,点B与B′是对应点,△A′B′C′周长为9
cm,AB=3
cm,BC=4
cm,则A′C′=2__cm.
5.如图,在图中的两个三角形是全等三角形,其中点A和D、点B和E是对应点.
(1)用符号表示两个三角形全等,并写出图中相等的线段;
(2)写出图中一组平行的线段,并说明理由.
解:(1)△ABC≌△DEF,AB=DE,BC=EF,AC=DF,AF=DC.
(2)∵△ABC≌△DEF,
∴∠A=∠D,
∴AB∥DE.
6.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.若DE=7,BC=4,∠D=35°,∠C=60°.
(1)求线段AE的长;
(2)求∠DFA的度数.
解:(1)∵△ABC≌△DEB,
∴DE=AB,BE=BC.
∵AE=AB-BE,
∴AE=DE-BC=7-4=3.
(2)∵△ABC≌△DEB,
∴∠A=∠D,∠C=∠DBE.
∴∠DEA=∠D+∠DBE=95°.
∴∠DFA=∠DEA+∠A=130°.
课堂小结
1.全等三角形的概念:能够完全重合的两个图形叫做全等形.平移、翻折、旋转前后的图形全等.
2.全等三角形:能够完全重合的两个三角形叫做全等三角形.
对应元素:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
表示方法:“全等”用“≌”表示,读作“全等于”,表示两个三角形全等时,通常把表示对顶点的字母写在对应的位置上.
3.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.
导学案
教学目标
1.知道什么是全等形、全等三角形及全等三角形的对应元素.
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等.
3.能熟练找出两个全等三角形的对应角、对应边.
预习反馈
阅读教材P31~32,完成下列内容.
1.全等形、全等三角形的概念:能够完全重合的两个图形叫做全等形;能够完全重合的两个三角形叫做全等三角形.如下列图形中的全等形是e与h、d与g.
2.把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
如图,△ABC与△DEF能重合,则记作:△ABC≌△DEF,对应顶点:点A与点D、点B与点E、点C与点F;对应边:AB与DE、AC与DF、BC与EF;对应角:∠A与∠D、∠B与∠E、∠C与∠F.
3.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.
如上图,△ABC≌△DEF,则AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F.
例题讲解
类型1 全等形的识别
例1 如图,在4个正方形图案中,与如图所示正方形图案全等的图案是(C)
【方法归纳】 判断全等形的方法:两个图形同时满足形状相同和大小相同才能称为全等形,并且全等形与它们的位置和方向无关.
【跟踪训练1】 在下列每组图形中,是全等形的是(C)
类型2 找全等三角形的对应元素
例2 如图,△ABC≌△DEF,点A与点D,点B和点E是对应顶点,写出这两个三角形的对应边和对应角.
解:由△ABC≌△DEF可得AC的对应边是DF,BC的对应边是EF,AB的对应边是DE,∠ABC的对应角是∠DEF,∠A的对应角是∠D,∠ACB的对应角是∠DFE.
【方法归纳】 确定全等三角形对应元素的三种方法:
1.字母顺序法:根据书写规范,按照对应顶点确定对应边,对应角.如:△ABC≌△DEF,则AB与DE,AC与DF,BC与EF是对应边,∠A和∠D,∠B和∠E,∠C和∠F是对应角.
2.图形位置法:①公共边一定是对应边;②公共角一定是对应角;③对顶角一定是对应角.
3.图形大小法:两个全等三角形的最大的边(角)是对应边(角),最小的边(角)是对应边(角).
【跟踪训练2】 如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
解:对应边:AN与AM,BN与CM;
对应角:∠BAN与∠CAM,∠ANB与∠AMC.
类型3 运用全等三角形的性质解决问题
例3 如图所示,△ABC绕着点B顺时针旋转90°得到△DBE,且∠ABC=90°.
(1)△ABC和△DBE是否全等?若全等,指出对应边和对应角;
(2)直线CD,DE有怎样的位置关系?
解:(1)∵△ABC绕着点B沿顺时针方向旋转90°得到△DBE,
∴△ABC≌△DBE.
∴∠BAC的对应角为∠BDE,∠ACB的对应角为∠DEB,∠ABC的对应角为∠DBE;AB的对应边为DB,BC的对应边为BE,AC的对应边为DE.
(2)AC⊥DE.
理由:延长AC,交DE于点F.
∵∠ABC=90°,∴∠A+∠1=90°.
又∵△ABC≌△DBE,∴∠D=∠A.
又∵∠2=∠1,∴∠2+∠D=90°.
∴AC⊥DE.
【方法归纳】 全等三角形的性质的用途
【跟踪训练3】 如图,把△ABC沿直线BA翻折至△ABD,那么△ABC和△ABD是全等图形(填“是”或“不是”).若CB=5,则DB=5;若△ABC的面积为10,则△ABD的面积为10.
巩固训练
1.下列关于全等三角形的说法,不正确的是(A)
A.形状相同的三角形是全等三角形
B.全等三角形的形状相同
C.全等三角形的大小相等
D.全等三角形的对应边相等
2.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是(C)
A.AC=CE
B.∠BAC=∠ECD
C.∠ACB=∠ECD
D.∠B=∠D
3.如图,若△OAD≌△OBC,∠COD=65°,∠C=20°,则∠OAD的度数为(D)
A.65°
B.75°
C.85°
D.95°
4.已知△ABC≌△A′B′C′,点A与A′,点B与B′是对应点,△A′B′C′周长为9
cm,AB=3
cm,BC=4
cm,则A′C′=2__cm.
5.如图,在图中的两个三角形是全等三角形,其中点A和D、点B和E是对应点.
(1)用符号表示两个三角形全等,并写出图中相等的线段;
(2)写出图中一组平行的线段,并说明理由.
解:(1)△ABC≌△DEF,AB=DE,BC=EF,AC=DF,AF=DC.
(2)∵△ABC≌△DEF,
∴∠A=∠D,
∴AB∥DE.
6.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.若DE=7,BC=4,∠D=35°,∠C=60°.
(1)求线段AE的长;
(2)求∠DFA的度数.
解:(1)∵△ABC≌△DEB,
∴DE=AB,BE=BC.
∵AE=AB-BE,
∴AE=DE-BC=7-4=3.
(2)∵△ABC≌△DEB,
∴∠A=∠D,∠C=∠DBE.
∴∠DEA=∠D+∠DBE=95°.
∴∠DFA=∠DEA+∠A=130°.
课堂小结
1.全等三角形的概念:能够完全重合的两个图形叫做全等形.平移、翻折、旋转前后的图形全等.
2.全等三角形:能够完全重合的两个三角形叫做全等三角形.
对应元素:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
表示方法:“全等”用“≌”表示,读作“全等于”,表示两个三角形全等时,通常把表示对顶点的字母写在对应的位置上.
3.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.
