人教版物理高中必修二5.1《曲线运动》(33张PPT)
文档属性
| 名称 | 人教版物理高中必修二5.1《曲线运动》(33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
§5-1曲线运动
曲线运动
物体运动轨迹为曲线的运动叫曲线运动。
曲线运动是普遍的运动情形。
大到宏观世界(如天体运行);
小到微观世界(如电子绕原子核旋转);
生活中如烟花、投标枪、铁饼、跳高、跳远等均为曲线运动。
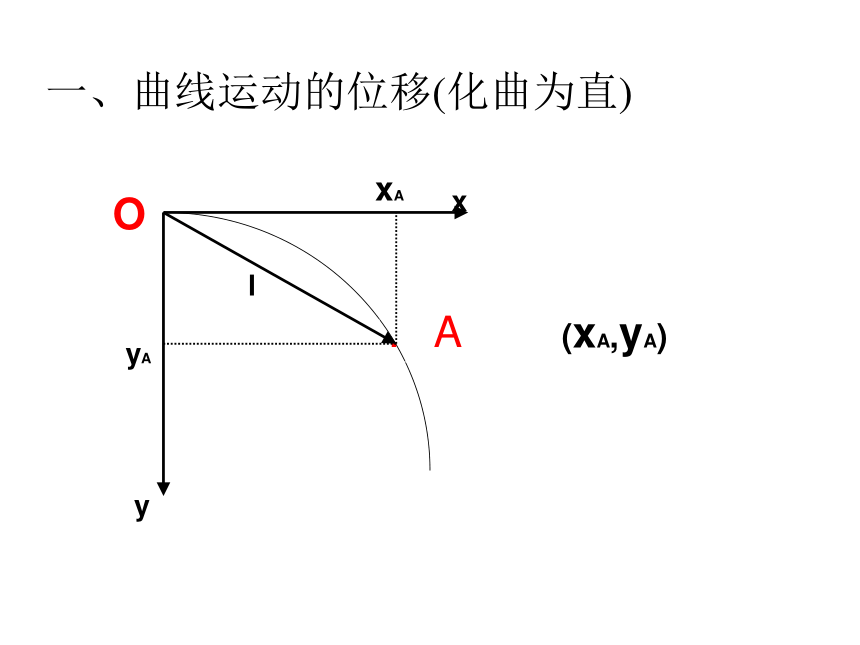
一、曲线运动的位移(化曲为直)
O
.
A
xA
yA
(xA,yA)
讨论
:
放手的位置不同,飞出去的方向相同吗?
说明了什么?
速度方向时刻改变
二、曲线运动的速度
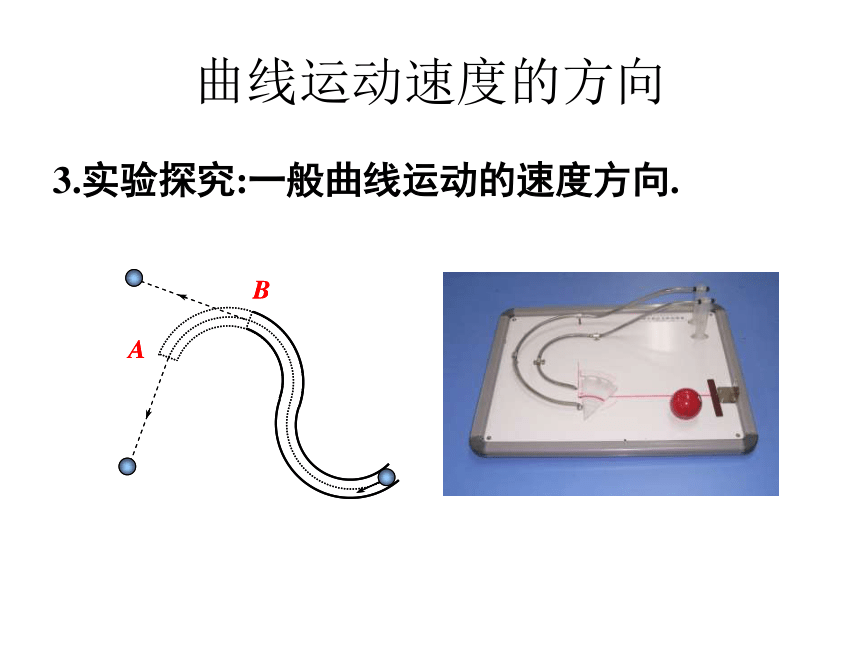
曲线运动速度的方向
3.实验探究:一般曲线运动的速度方向.
曲线运动速度的方向
理论探究:
从平均速度到瞬时速度(从割线到切线).
质点在某一点的速度,沿曲线在这一点的切线方向.
结论:
质点在某一点(或某一时刻)的速度方向在曲线的这一点的切线方向上。
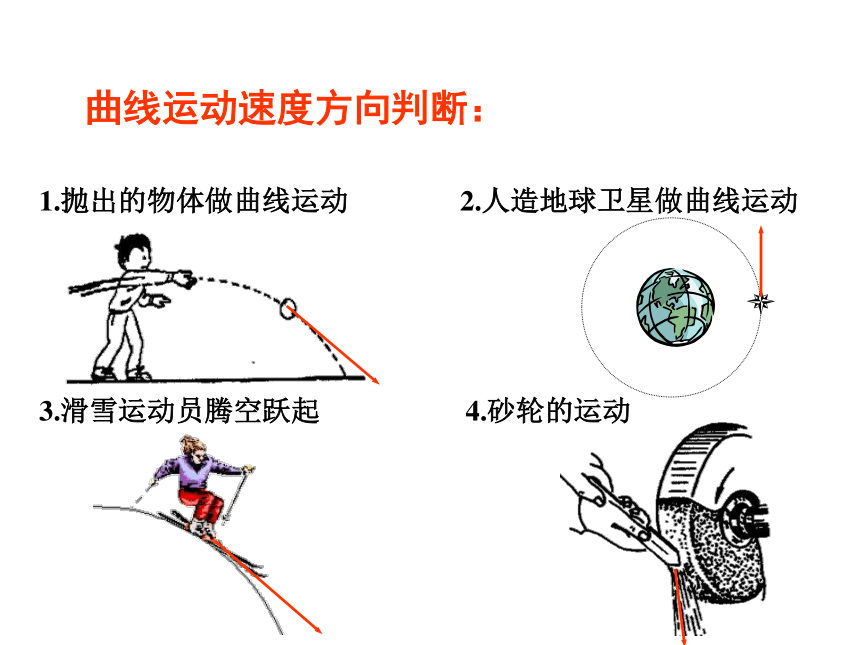
2.人造地球卫星做曲线运动
1.抛出的物体做曲线运动
3.滑雪运动员腾空跃起
4.砂轮的运动
曲线运动速度方向判断:
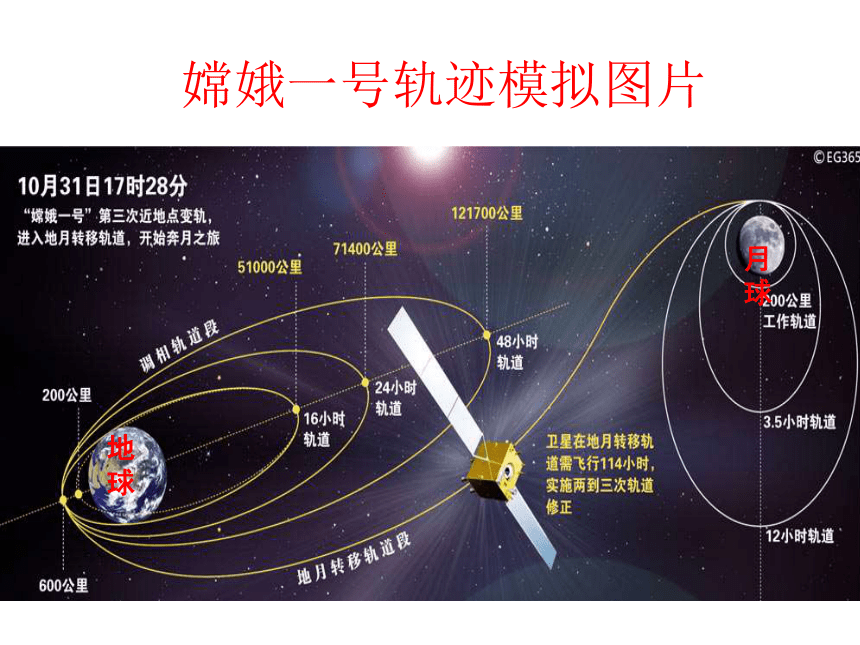
嫦娥一号轨迹模拟图片
地球
月球
曲线运动的性质
1、曲线运动的速度方向在时刻发生变化
曲线运动是变速运动,但变速运动不一定是曲线运动;
2、曲线运动速度的大小一定要变化吗?
不一定,但方向一定变化
3、曲线运动的速度方向时刻发生变化,故加速度不为0,即做曲线运动的物体的合力一定不为零。
3.曲线运动的运动性质
曲线运动中,至少速度的
方向会改变
=>
速度一定改变
=>
一定存在加速度a
所以,曲线运动一定是变速运动。(变速运动不一定是曲线运动),曲线运动一定是变速运动。
研究物体的曲线运动,可以建立一个
平面直角坐标系。
位移的描述:物体运动到某点时,尽量用它在坐标轴方向的分矢量来表示,而分矢量可用该点的坐标表示
速度的描述:可以用相互垂直的两个方向的分矢量来表示,这两个分矢量叫做分速度
曲线运动的特点
①轨迹是曲线
②某点的瞬时速度方向就是该点的切线方向
③速度方向时刻在改变,曲线运动是变速运动必有加速度
一个在水平面上做直线运动的钢球,从旁边给它一个力,例如在钢球运动路线的旁边放一块磁铁,观察钢球的运动。
二、物体做曲线运动的条件
如何使小钢球做加速直线运动?
施加的力F的方向与小钢球的速度V的方向一致。
1.回忆
如何使小钢球做减速直线运动?
施加的力F的方向与小钢球的速度V的方向相反。
思考总结:物体做直线运动的条件?
合力(或加速度)与速度在一条直线上
问题:物体在什么条件下做曲线运动?
2.物体做曲线运动的条件(无力不拐弯,拐弯必有力)
合力的方向与它的速度方向不在同一直线上
物体的加速度方向与速度方向不在同一直线上
(1).从力的角度来说:
(2).从运动学的角度来说:
(3).合力的方向特征:
做曲线运动的物体,合力指向哪里,曲线向哪里弯曲(合力指向曲线的内侧)
力与速度的关系
①平行速度的力改变速度大小;
②垂直速度的力改变速度方向;
③不平行也不垂直速度的力,同时改变速度的大小和方向;
三、平面中运动描述的实例
蜡块的运动
蜡块参与的运动
竖直向上:
水平向右:
合探:
蜡块的实际运动还是匀速直线运动吗?
匀速直线运动
匀速直线运动
1、蜡块的位置坐标
(1)、建立直角坐标系:
运动的开始位置为坐标原点;
水平向右的方向为x轴;
竖直向上的方向为y轴。
(2)、设蜡块沿玻璃管匀速上升的速度为vy,玻璃管向右运动的速度为vx,从蜡块开始运动计时,在t时刻蜡块的位置坐标为:
x=vxt
y=vyt
2、蜡块的速度
方向:与x轴之间的夹角θ
蜡块的实际速度不变。
3、蜡块的运动轨迹
由
x=vxt
y=vyt
得到:
结论:蜡块的运动轨迹是一条直线
所以,蜡块的实际运动还是匀速直线运动。
合运动与分运动:如果一个物体同时参与了两种运动,这两个运动叫做分运动,而物体相对地面的实际运动就是合运动,实际运动的方向就是合运动的方向
四.运动的合成与分解
1.合运动与分运动
合运动:物体的实际运动
分运动:用来等效替代实际运动的几个运动
2.合运动与分运动之间的关系
b.等时性
c.分运动的独立性
a.合运动与分运动的等效性
注:合运动与分运动并非并存关系
d.运动的合成与分解实质是位移、加速度、速度的分解,所以都遵循平行四边行定则
五:两个互成角度的直线运动的合运动
1.两个匀速直线运动合成为
2.一个匀速直线运动与一个匀变速直线运动合成为
3.两个初速度不为零匀变速直线运动的合运动为
匀速直线运动
匀变速曲线运动
匀变速直线运动
或匀变速曲线运动
六.曲线运动的研究方法
按实际作用效果分解将物体的实际运动(即合运动)分解成我们比较熟悉的直线运动。
(一)小船渡河问题
1.先确定合运动和分运动
小船的实际运动(站在岸上的人看到的运动)为合运动;同时参与的两个分运动中,一个是船相对于静水的运动,它的方向与船身指向相同,另一个是船随水漂流的运动,它的方向与河岸平行,船在水中的合运动(实际相对地面的运动)是上述两个分运动的合成.
七:运动描述的实例
2.分情况讨论小船渡河问题
第一种情况:船速大于水速,即v2>v1.(设水流速度为v1,船在静水中速度为v2,河宽为d)
(1)怎样才能使渡河时间最短
由分运动与合运动的等时性知,让船头垂直对岸运动即可(如下图所示)
船头的指向与船
的实际航向不同
(2)怎样才能使渡河位移最短
小船的运动为实际运动,要使实际运动位移
最短只要使合位移最短即可,位移最短为河宽d,
船头须向上游倾斜一定角度(如下图所示)
第二种情况:船速小于水速,即:V2(1)怎样才能使渡河时间最短
只要使船头沿垂直对岸航行就可以
(2)怎样使渡河位移最短
绳及杆的速度分解
沿绳方向使绳伸长
垂直于绳方向使绳转动
绳(杆)模型绳(杆)端速度分解原则:
沿着绳(杆)和垂直绳(杆)
则V与V1的关系为
?
注:绳(杆)两端速度大小一般不相等,但两端沿绳(杆)方向速度一定相等※
V1=VCOSθ
【例题】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为θ时,物体B的速率为
。
【答案】
vB=vsinθ
寻找分运动效果
“绳+物”问题
【例题】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2
m/s,这时B的速度为
。
寻找分运动效果
【答案】
“绳+物”问题
【例题】如图所示,杆AB它的两端在地板和竖直墙壁上,现拉A端由图示位置以速率v匀速向右运动,B端滑动的速度是
。
寻找分运动效果
“杆+物”问题
α
Vcosθ
VBcosα
【例题】如图所示,滑块B以速度vB向左运动时,触点P的沿杆移动的速度如何?
【答案】
寻找分运动效果
“杆+物”问题
运动的合成与分解是指
x、v、
a
的合成与分解。
速度、位移、加速度都是矢量,合成与分解时均遵循平行四边形定则
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
§5-1曲线运动
曲线运动
物体运动轨迹为曲线的运动叫曲线运动。
曲线运动是普遍的运动情形。
大到宏观世界(如天体运行);
小到微观世界(如电子绕原子核旋转);
生活中如烟花、投标枪、铁饼、跳高、跳远等均为曲线运动。
一、曲线运动的位移(化曲为直)
O
.
A
xA
yA
(xA,yA)
讨论
:
放手的位置不同,飞出去的方向相同吗?
说明了什么?
速度方向时刻改变
二、曲线运动的速度
曲线运动速度的方向
3.实验探究:一般曲线运动的速度方向.
曲线运动速度的方向
理论探究:
从平均速度到瞬时速度(从割线到切线).
质点在某一点的速度,沿曲线在这一点的切线方向.
结论:
质点在某一点(或某一时刻)的速度方向在曲线的这一点的切线方向上。
2.人造地球卫星做曲线运动
1.抛出的物体做曲线运动
3.滑雪运动员腾空跃起
4.砂轮的运动
曲线运动速度方向判断:
嫦娥一号轨迹模拟图片
地球
月球
曲线运动的性质
1、曲线运动的速度方向在时刻发生变化
曲线运动是变速运动,但变速运动不一定是曲线运动;
2、曲线运动速度的大小一定要变化吗?
不一定,但方向一定变化
3、曲线运动的速度方向时刻发生变化,故加速度不为0,即做曲线运动的物体的合力一定不为零。
3.曲线运动的运动性质
曲线运动中,至少速度的
方向会改变
=>
速度一定改变
=>
一定存在加速度a
所以,曲线运动一定是变速运动。(变速运动不一定是曲线运动),曲线运动一定是变速运动。
研究物体的曲线运动,可以建立一个
平面直角坐标系。
位移的描述:物体运动到某点时,尽量用它在坐标轴方向的分矢量来表示,而分矢量可用该点的坐标表示
速度的描述:可以用相互垂直的两个方向的分矢量来表示,这两个分矢量叫做分速度
曲线运动的特点
①轨迹是曲线
②某点的瞬时速度方向就是该点的切线方向
③速度方向时刻在改变,曲线运动是变速运动必有加速度
一个在水平面上做直线运动的钢球,从旁边给它一个力,例如在钢球运动路线的旁边放一块磁铁,观察钢球的运动。
二、物体做曲线运动的条件
如何使小钢球做加速直线运动?
施加的力F的方向与小钢球的速度V的方向一致。
1.回忆
如何使小钢球做减速直线运动?
施加的力F的方向与小钢球的速度V的方向相反。
思考总结:物体做直线运动的条件?
合力(或加速度)与速度在一条直线上
问题:物体在什么条件下做曲线运动?
2.物体做曲线运动的条件(无力不拐弯,拐弯必有力)
合力的方向与它的速度方向不在同一直线上
物体的加速度方向与速度方向不在同一直线上
(1).从力的角度来说:
(2).从运动学的角度来说:
(3).合力的方向特征:
做曲线运动的物体,合力指向哪里,曲线向哪里弯曲(合力指向曲线的内侧)
力与速度的关系
①平行速度的力改变速度大小;
②垂直速度的力改变速度方向;
③不平行也不垂直速度的力,同时改变速度的大小和方向;
三、平面中运动描述的实例
蜡块的运动
蜡块参与的运动
竖直向上:
水平向右:
合探:
蜡块的实际运动还是匀速直线运动吗?
匀速直线运动
匀速直线运动
1、蜡块的位置坐标
(1)、建立直角坐标系:
运动的开始位置为坐标原点;
水平向右的方向为x轴;
竖直向上的方向为y轴。
(2)、设蜡块沿玻璃管匀速上升的速度为vy,玻璃管向右运动的速度为vx,从蜡块开始运动计时,在t时刻蜡块的位置坐标为:
x=vxt
y=vyt
2、蜡块的速度
方向:与x轴之间的夹角θ
蜡块的实际速度不变。
3、蜡块的运动轨迹
由
x=vxt
y=vyt
得到:
结论:蜡块的运动轨迹是一条直线
所以,蜡块的实际运动还是匀速直线运动。
合运动与分运动:如果一个物体同时参与了两种运动,这两个运动叫做分运动,而物体相对地面的实际运动就是合运动,实际运动的方向就是合运动的方向
四.运动的合成与分解
1.合运动与分运动
合运动:物体的实际运动
分运动:用来等效替代实际运动的几个运动
2.合运动与分运动之间的关系
b.等时性
c.分运动的独立性
a.合运动与分运动的等效性
注:合运动与分运动并非并存关系
d.运动的合成与分解实质是位移、加速度、速度的分解,所以都遵循平行四边行定则
五:两个互成角度的直线运动的合运动
1.两个匀速直线运动合成为
2.一个匀速直线运动与一个匀变速直线运动合成为
3.两个初速度不为零匀变速直线运动的合运动为
匀速直线运动
匀变速曲线运动
匀变速直线运动
或匀变速曲线运动
六.曲线运动的研究方法
按实际作用效果分解将物体的实际运动(即合运动)分解成我们比较熟悉的直线运动。
(一)小船渡河问题
1.先确定合运动和分运动
小船的实际运动(站在岸上的人看到的运动)为合运动;同时参与的两个分运动中,一个是船相对于静水的运动,它的方向与船身指向相同,另一个是船随水漂流的运动,它的方向与河岸平行,船在水中的合运动(实际相对地面的运动)是上述两个分运动的合成.
七:运动描述的实例
2.分情况讨论小船渡河问题
第一种情况:船速大于水速,即v2>v1.(设水流速度为v1,船在静水中速度为v2,河宽为d)
(1)怎样才能使渡河时间最短
由分运动与合运动的等时性知,让船头垂直对岸运动即可(如下图所示)
船头的指向与船
的实际航向不同
(2)怎样才能使渡河位移最短
小船的运动为实际运动,要使实际运动位移
最短只要使合位移最短即可,位移最短为河宽d,
船头须向上游倾斜一定角度(如下图所示)
第二种情况:船速小于水速,即:V2
只要使船头沿垂直对岸航行就可以
(2)怎样使渡河位移最短
绳及杆的速度分解
沿绳方向使绳伸长
垂直于绳方向使绳转动
绳(杆)模型绳(杆)端速度分解原则:
沿着绳(杆)和垂直绳(杆)
则V与V1的关系为
?
注:绳(杆)两端速度大小一般不相等,但两端沿绳(杆)方向速度一定相等※
V1=VCOSθ
【例题】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为θ时,物体B的速率为
。
【答案】
vB=vsinθ
寻找分运动效果
“绳+物”问题
【例题】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2
m/s,这时B的速度为
。
寻找分运动效果
【答案】
“绳+物”问题
【例题】如图所示,杆AB它的两端在地板和竖直墙壁上,现拉A端由图示位置以速率v匀速向右运动,B端滑动的速度是
。
寻找分运动效果
“杆+物”问题
α
Vcosθ
VBcosα
【例题】如图所示,滑块B以速度vB向左运动时,触点P的沿杆移动的速度如何?
【答案】
寻找分运动效果
“杆+物”问题
运动的合成与分解是指
x、v、
a
的合成与分解。
速度、位移、加速度都是矢量,合成与分解时均遵循平行四边形定则
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
