沪科版八年级数学上册第十五章15.3.1等腰三角形的性质说课课件 (共26张PPT)
文档属性
| 名称 | 沪科版八年级数学上册第十五章15.3.1等腰三角形的性质说课课件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 22:19:40 | ||
图片预览





文档简介
(共26张PPT)
15.3
等腰三角形
15.3.1等腰三角形的性质
设计意图:激发学习兴趣,引入新课
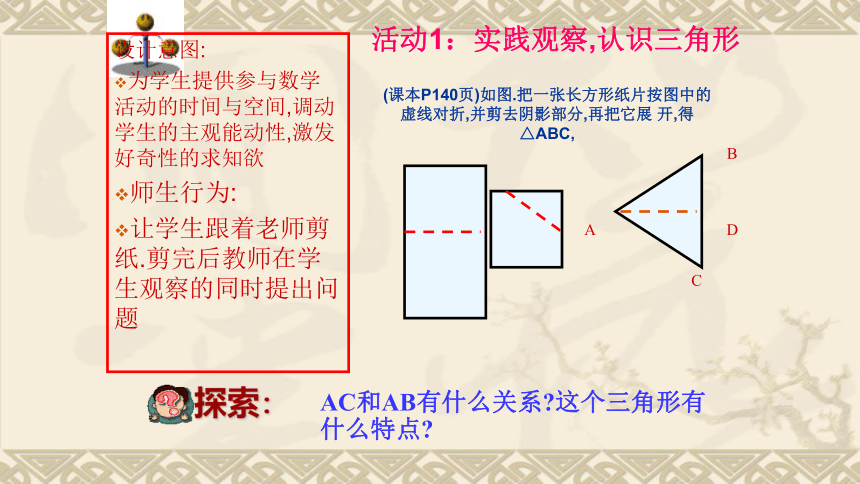
(课本P140页)如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展
开,得△ABC,
活动1:实践观察,认识三角形
A
C
D
B
AC和AB有什么关系?这个三角形有什么特点?
探索:
设计意图:
为学生提供参与数学活动的时间与空间,调动学生的主观能动性,激发好奇性的求知欲
师生行为:
让学生跟着老师剪纸.剪完后教师在学生观察的同时提出问题
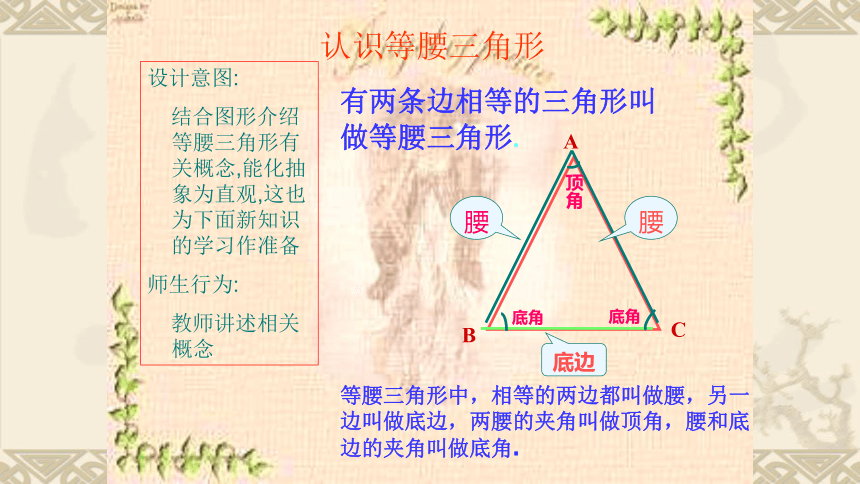
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
设计意图:
结合图形介绍等腰三角形有关概念,能化抽象为直观,这也为下面新知识的学习作准备
师生行为:
教师讲述相关概念
认识等腰三角形
设计意图:
为学生提供参与数学活动的时间与空间,调动学生的主观能动性,激发好奇性的求知欲,培养”探究”能力,以及合作交流习惯
师生行为:
教师在学生充分发表自己想法的基础上给出画图方法,为了体现画图过程,因此在黑板上画出图形,介绍腰,底,顶角,底角
讨论:除了剪纸的方法,还可以怎样作(画)出一个等腰三角形?在你作(画)出的等腰三角形中,指明它的腰,底边,顶角的底角
活动2:探索等腰三角形性质
上面剪出的等腰三角形是轴对称图形吗?
把剪出的等腰三角形ABC沿折痕AD对折,找出其中相等的线段和角,填入下表
重合的线段
重合的角
A
C
D
B
设计意图:
通过学生的动手实践,观察思考,,培养学生自主探究学习的能力,使用几何画板课件演示能帮助学生更易理解和探索出”三线合一”这性质
师生行为:
学生动手折纸,观察,找出重合的线段和角,填写表格,
(学生可能不能准确填写)同时为了使学生更容易观察出“三线合一”这性质,教师再演示课件,引导学生准确地填好表格
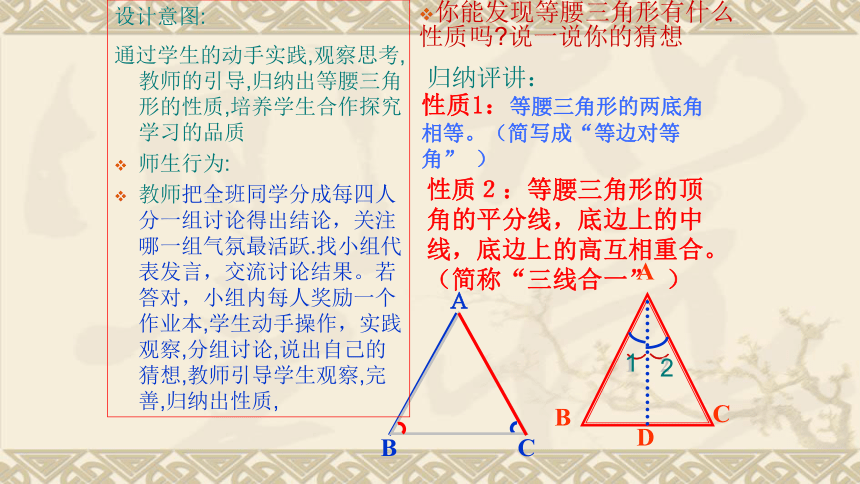
你能发现等腰三角形有什么性质吗?说一说你的猜想
性质1:等腰三角形的两底角相等。(简写成“等边对等角”
)
C
B
A
归纳评讲:
设计意图:
通过学生的动手实践,观察思考,教师的引导,归纳出等腰三角形的性质,培养学生合作探究学习的品质
师生行为:
教师把全班同学分成每四人分一组讨论得出结论,关注哪一组气氛最活跃.找小组代表发言,交流讨论结果。若答对,小组内每人奖励一个作业本,学生动手操作,实践观察,分组讨论,说出自己的猜想,教师引导学生观察,完善,归纳出性质,
性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”
)
A
B
C
D
⌒
⌒
1
2
1
2
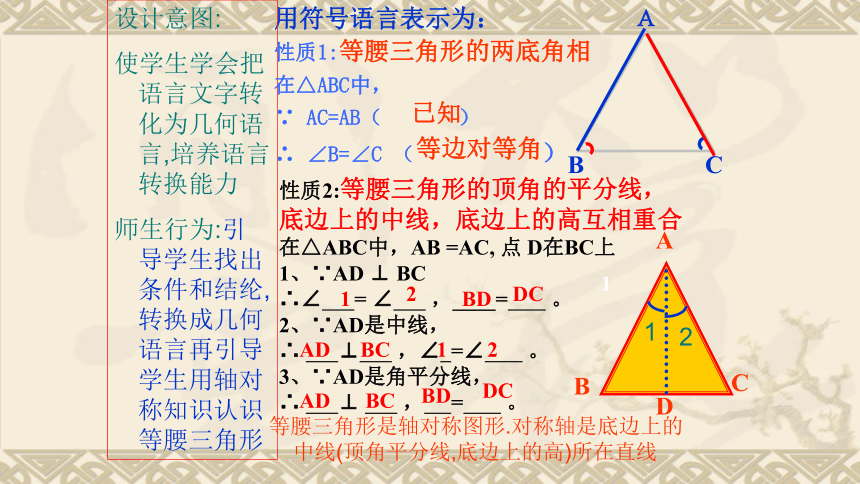
性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合
在△ABC中,AB
=AC,
点
D在BC上
1、∵AD
⊥
BC
∴∠
=
∠
,____=
。
2、∵AD是中线,
∴
⊥
,∠
=∠
。
3、∵AD是角平分线,
∴
⊥
,
=
。
1
1
2
BD
DC
AD
BC
1
2
AD
BC
BD
DC
用符号语言表示为:
设计意图:
使学生学会把语言文字转化为几何语言,培养语言转换能力
师生行为:引导学生找出条件和结纶,转换成几何语言再引导学生用轴对称知识认识等腰三角形
等腰三角形是轴对称图形.对称轴是底边上的中线(顶角平分线,底边上的高)所在直线
A
B
C
D
⌒
⌒
1
2
1
2
性质1:等腰三角形的两底角相
在△ABC中,
∵
AC=AB(
)
∴
∠B=∠C
(
)
已知
等边对等角
C
B
A
设计意图:
增强理性认识,体验性质的正确性,提高演绎推理能力
教师引导学生找出条件和结论,并转换成数学符号,利用全等三角形性质,根据对称性寻找辅助线的添加方法,师生共同完成证明过程
证明性质1:等腰三角形的两个底角相等
(等边对等角)
。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
证明:在△ABC中,AB=AC,作底边
BC的中线AD,
在
△
BAD
与△
CAD
中
∵
AB=___
BD=___
AD=___
∴
△
BAD
≌△
CAD(
)
∠B=
___
AC
∠C
CD
AD
SSS
A
B
C
D
提问:这性质的条件和结论是什么?用数学符号如何表达条件和结论?
活动3:等腰三角形性质定理的证明
设计意图:
增强理性认识,体验性质的正确性,提高演绎推理能力
师生行为:
教师引导学生根据条件和结论写出已知和求证,分析证明思路后,学生表达,教师板书,教师关注学生语言规范性,应用意识,模仿能力,发表个人见解勇气,鼓励学生说出其它证明方法(因为时间有限只能师生共同完成)
方法1:已知:△ABC中,AB=AC,AD是△ABC
的中线
证明性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”
)
求证:AD是△ABC的高和角平分线
证明:
∵,AD是△ABC的中线
∴BD=CD
在△
BAD
≌△
CAD中
∵
AB=AC
BD=CD
AD=
AD
∴
△
BAD
≌△
CAD(
SSS
)
∠BAD=
CAD;
∠BDA=
CDA
∴AD是△ABC是角平分线
又∵
∠BDA+
CDA=1800
∴
∠BDA=CDA=900
∴
AD是△ABC的高
A
B
C
D
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△
ABC各角的度数
设计意图:
培养学生正确应用所学知识的能力,增强应用意识,参与意识,巩固所学性质
师生行为:
教师分析解题思路后,学生表达,教师板书
解:AB=AC,BD=BC=AD,
∠
ABC=
∠
C=
∠
BDC
∠
A=
∠
ADD(等边对等角)
设A=x,则
∠
BDC=
∠
A+
∠
ABD=2x
从而∠
ABC=
∠
C=
∠
BDC=2x
于是在△
ABC中,有
∠
A+
∠
ABC+
∠
C=x+2x+2x=1800.
解得x=360
在△
ABC中,
∠
A=360
∠,ABC=
∠
C=720
B
C
A
D
活动4:等腰三角形性质定理的运用
练习1:小试牛刀
如图(1)在等腰△ABC中,
AB
=AC,
∠A
=
36°,则∠B
=——∠C=—
变式练习:
1、如图(2)在等△ABC腰中,∠A
=
50°,
则∠B
=——,∠C=——
2、如图(3)在等△ABC腰中,∠A
=
120°则∠B
=——,∠C=——
C
B
A
图1
C
B
A
图2
C
A
B
图3
设计意图:
及时巩固所学知识,了解学习效果,增强学生应用知识的能力,同时培养学生分类讨论的思想
师生行为:
学生独立完成
教师找学生口答,点评
活动5:反馈练习
练习2:
△
ABC是等腰直角三角形(AB=AC,
∠
BAC=90°),AD是底边BC上的高,标出∠
B,
∠
C,
∠
BAD,
∠
DAC的度数,图中有哪些相等的线段?
练习3:在△
ABC中,AB=AD=DC,
∠BAD=26°,求∠
B和∠
C的度数
B
A
C
D
B
D
C
A
设计意图:
为了使学生巩固基础知识,掌握基本技能,拓展提高思维能力,让每个学生都能尝到成功的喜悦,设计成三个档次去练习
师生行为:
学生独立完成
教师让学生板演,并点评
摩拳擦掌
设计意图:
通过学生动手实践,增强动手能力,启发学生发散思维能力
师生行为:小组讨论,代表回答
教师指导学生画图,折纸,得出结论,指导学生寻找出等腰三角形其它相等的线段
猜想一下,等腰三角形底边中点到两腰的距离相等吗?
如图,你可以将等腰三角形ABC沿对称轴AD折叠,观察DE与DF的关系。
如果DE,DF分别是AB,AC上的中线或∠
ADB,
∠
ADC的平分线,它们还相等吗?由等腰三角形是轴对称图形,利用类似的方法,还可以得到等腰三角形中哪些线段相等?
A
E
B
C
D
F
A
C
D
B
F
E
评讲归纳:等腰三角形两腰上的高,中线,两底角平分线,底边上的中点到两腰的距离相等
活动6讨论探究:
A
C
B
腰
腰
底边
顶角
底角
底角
概念
如图△ABC,AB=AC.
等腰三角形的性质(猜想):
A
C
B
1
2
1
.等腰三角形的两个底角相等
(简写“等边对等角”)。
A
B
C
1
2
已知:
△ABC中,
AB=AC,
求证:∠B=∠C。
探究与证明:
D
等腰三角形的性质:
定理1:等腰三角形的两个底角相等
(简写成“等边对等角”)
注:在
三角形中,等边对等角。
同一个或全等
C
A
B
符号语言表示:
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
思考:根据定理1:等边对等角可得等边三角形的三个内角有怎样的数量关系?
推论:等边三角形三个内角相等,每个内角等于60°
C
A
B
1
2
D
等腰三角形的性质:
定理2:等腰三角形顶角的平分线垂直平分底边。
(等腰三角形顶角的平分线,底边上的
中线,底边上的高
“三线合一”)
符号语言表示:
∵AB=AC,∠BAD=∠CAD
∴AD⊥BC,BD=CD
如图在△ABC中,点
D在BC上
1、∵
AB
=AC,
AD
⊥
BC
∴∠1=∠__
,BD=
__
2、∵
AB
=AC,
BD=CD
∴
__
⊥
__
,
∠__
=
∠2
。
2
CD
AD
BC
1
建筑工人在盖房子时,用一块等腰三
角板放在梁上,从顶点系一重物,如果系
重物的绳子正好经过三角板底边中点,就
说房梁是水平的,你知道其中反映了什么
数学原理?
应用新知:
巩固新知:
1.填空
(1)等腰直角三角形的每一个锐角的度数是___;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是_____;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的顶角等于___________。
45°
100°
80
°或20°
例1
已知:如图,在△ABC中,AB=AC,∠BAC=
120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数。
A
B
D
E
C
同理∠2=∠C=
30°
∴∠DAE=∠BAC-(∠1+∠2)
=
120°-
(30°+
30°)
=
60°
解:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C=
×(180°-
120°)
=
30°
又∵BD=AD
(已知)
∴∠1=∠B=
30°
(等边对等角)
2
1
—
例题讲解
1
2
A
B
D
E
C
2
1
解:
∵
∠BAC=
120°
∴∠B+
∠C=180
°-
∠BAC
=60
°
∵
AD=BD
∴∠B=∠1(等边对等角)
同理:
∠C=
∠2
∠1+
∠2=
∠B+
∠C=60
°
∴∠DAE=∠BAC-(∠1+∠2)
=
120°-60
°
=60
°
如图,AD是等腰三角形ABC的顶角平分线,E是AB上的点,请在AD上找一点P,使PE+PB的值最小.
B
C
E
A
●
D
思考
P
●
┐
课堂小结
等腰三角形的性质
等腰三角形
三线合一
1、求有关等腰三角形的问题,作
顶角平分线、底边中线,底边的
高是常用的辅助线;
2、熟练掌握求解等腰三角形的顶
角、底角的度数;
3、掌握等腰三角形三线合一的
应用。
等边对等角
这节课我们学习了什么?
谈谈你的收获和疑惑!
作
业:
习题
15.3
P139
1,2,3,5
15.3
等腰三角形
15.3.1等腰三角形的性质
设计意图:激发学习兴趣,引入新课
(课本P140页)如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展
开,得△ABC,
活动1:实践观察,认识三角形
A
C
D
B
AC和AB有什么关系?这个三角形有什么特点?
探索:
设计意图:
为学生提供参与数学活动的时间与空间,调动学生的主观能动性,激发好奇性的求知欲
师生行为:
让学生跟着老师剪纸.剪完后教师在学生观察的同时提出问题
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
设计意图:
结合图形介绍等腰三角形有关概念,能化抽象为直观,这也为下面新知识的学习作准备
师生行为:
教师讲述相关概念
认识等腰三角形
设计意图:
为学生提供参与数学活动的时间与空间,调动学生的主观能动性,激发好奇性的求知欲,培养”探究”能力,以及合作交流习惯
师生行为:
教师在学生充分发表自己想法的基础上给出画图方法,为了体现画图过程,因此在黑板上画出图形,介绍腰,底,顶角,底角
讨论:除了剪纸的方法,还可以怎样作(画)出一个等腰三角形?在你作(画)出的等腰三角形中,指明它的腰,底边,顶角的底角
活动2:探索等腰三角形性质
上面剪出的等腰三角形是轴对称图形吗?
把剪出的等腰三角形ABC沿折痕AD对折,找出其中相等的线段和角,填入下表
重合的线段
重合的角
A
C
D
B
设计意图:
通过学生的动手实践,观察思考,,培养学生自主探究学习的能力,使用几何画板课件演示能帮助学生更易理解和探索出”三线合一”这性质
师生行为:
学生动手折纸,观察,找出重合的线段和角,填写表格,
(学生可能不能准确填写)同时为了使学生更容易观察出“三线合一”这性质,教师再演示课件,引导学生准确地填好表格
你能发现等腰三角形有什么性质吗?说一说你的猜想
性质1:等腰三角形的两底角相等。(简写成“等边对等角”
)
C
B
A
归纳评讲:
设计意图:
通过学生的动手实践,观察思考,教师的引导,归纳出等腰三角形的性质,培养学生合作探究学习的品质
师生行为:
教师把全班同学分成每四人分一组讨论得出结论,关注哪一组气氛最活跃.找小组代表发言,交流讨论结果。若答对,小组内每人奖励一个作业本,学生动手操作,实践观察,分组讨论,说出自己的猜想,教师引导学生观察,完善,归纳出性质,
性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”
)
A
B
C
D
⌒
⌒
1
2
1
2
性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合
在△ABC中,AB
=AC,
点
D在BC上
1、∵AD
⊥
BC
∴∠
=
∠
,____=
。
2、∵AD是中线,
∴
⊥
,∠
=∠
。
3、∵AD是角平分线,
∴
⊥
,
=
。
1
1
2
BD
DC
AD
BC
1
2
AD
BC
BD
DC
用符号语言表示为:
设计意图:
使学生学会把语言文字转化为几何语言,培养语言转换能力
师生行为:引导学生找出条件和结纶,转换成几何语言再引导学生用轴对称知识认识等腰三角形
等腰三角形是轴对称图形.对称轴是底边上的中线(顶角平分线,底边上的高)所在直线
A
B
C
D
⌒
⌒
1
2
1
2
性质1:等腰三角形的两底角相
在△ABC中,
∵
AC=AB(
)
∴
∠B=∠C
(
)
已知
等边对等角
C
B
A
设计意图:
增强理性认识,体验性质的正确性,提高演绎推理能力
教师引导学生找出条件和结论,并转换成数学符号,利用全等三角形性质,根据对称性寻找辅助线的添加方法,师生共同完成证明过程
证明性质1:等腰三角形的两个底角相等
(等边对等角)
。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
证明:在△ABC中,AB=AC,作底边
BC的中线AD,
在
△
BAD
与△
CAD
中
∵
AB=___
BD=___
AD=___
∴
△
BAD
≌△
CAD(
)
∠B=
___
AC
∠C
CD
AD
SSS
A
B
C
D
提问:这性质的条件和结论是什么?用数学符号如何表达条件和结论?
活动3:等腰三角形性质定理的证明
设计意图:
增强理性认识,体验性质的正确性,提高演绎推理能力
师生行为:
教师引导学生根据条件和结论写出已知和求证,分析证明思路后,学生表达,教师板书,教师关注学生语言规范性,应用意识,模仿能力,发表个人见解勇气,鼓励学生说出其它证明方法(因为时间有限只能师生共同完成)
方法1:已知:△ABC中,AB=AC,AD是△ABC
的中线
证明性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”
)
求证:AD是△ABC的高和角平分线
证明:
∵,AD是△ABC的中线
∴BD=CD
在△
BAD
≌△
CAD中
∵
AB=AC
BD=CD
AD=
AD
∴
△
BAD
≌△
CAD(
SSS
)
∠BAD=
CAD;
∠BDA=
CDA
∴AD是△ABC是角平分线
又∵
∠BDA+
CDA=1800
∴
∠BDA=CDA=900
∴
AD是△ABC的高
A
B
C
D
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△
ABC各角的度数
设计意图:
培养学生正确应用所学知识的能力,增强应用意识,参与意识,巩固所学性质
师生行为:
教师分析解题思路后,学生表达,教师板书
解:AB=AC,BD=BC=AD,
∠
ABC=
∠
C=
∠
BDC
∠
A=
∠
ADD(等边对等角)
设A=x,则
∠
BDC=
∠
A+
∠
ABD=2x
从而∠
ABC=
∠
C=
∠
BDC=2x
于是在△
ABC中,有
∠
A+
∠
ABC+
∠
C=x+2x+2x=1800.
解得x=360
在△
ABC中,
∠
A=360
∠,ABC=
∠
C=720
B
C
A
D
活动4:等腰三角形性质定理的运用
练习1:小试牛刀
如图(1)在等腰△ABC中,
AB
=AC,
∠A
=
36°,则∠B
=——∠C=—
变式练习:
1、如图(2)在等△ABC腰中,∠A
=
50°,
则∠B
=——,∠C=——
2、如图(3)在等△ABC腰中,∠A
=
120°则∠B
=——,∠C=——
C
B
A
图1
C
B
A
图2
C
A
B
图3
设计意图:
及时巩固所学知识,了解学习效果,增强学生应用知识的能力,同时培养学生分类讨论的思想
师生行为:
学生独立完成
教师找学生口答,点评
活动5:反馈练习
练习2:
△
ABC是等腰直角三角形(AB=AC,
∠
BAC=90°),AD是底边BC上的高,标出∠
B,
∠
C,
∠
BAD,
∠
DAC的度数,图中有哪些相等的线段?
练习3:在△
ABC中,AB=AD=DC,
∠BAD=26°,求∠
B和∠
C的度数
B
A
C
D
B
D
C
A
设计意图:
为了使学生巩固基础知识,掌握基本技能,拓展提高思维能力,让每个学生都能尝到成功的喜悦,设计成三个档次去练习
师生行为:
学生独立完成
教师让学生板演,并点评
摩拳擦掌
设计意图:
通过学生动手实践,增强动手能力,启发学生发散思维能力
师生行为:小组讨论,代表回答
教师指导学生画图,折纸,得出结论,指导学生寻找出等腰三角形其它相等的线段
猜想一下,等腰三角形底边中点到两腰的距离相等吗?
如图,你可以将等腰三角形ABC沿对称轴AD折叠,观察DE与DF的关系。
如果DE,DF分别是AB,AC上的中线或∠
ADB,
∠
ADC的平分线,它们还相等吗?由等腰三角形是轴对称图形,利用类似的方法,还可以得到等腰三角形中哪些线段相等?
A
E
B
C
D
F
A
C
D
B
F
E
评讲归纳:等腰三角形两腰上的高,中线,两底角平分线,底边上的中点到两腰的距离相等
活动6讨论探究:
A
C
B
腰
腰
底边
顶角
底角
底角
概念
如图△ABC,AB=AC.
等腰三角形的性质(猜想):
A
C
B
1
2
1
.等腰三角形的两个底角相等
(简写“等边对等角”)。
A
B
C
1
2
已知:
△ABC中,
AB=AC,
求证:∠B=∠C。
探究与证明:
D
等腰三角形的性质:
定理1:等腰三角形的两个底角相等
(简写成“等边对等角”)
注:在
三角形中,等边对等角。
同一个或全等
C
A
B
符号语言表示:
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
思考:根据定理1:等边对等角可得等边三角形的三个内角有怎样的数量关系?
推论:等边三角形三个内角相等,每个内角等于60°
C
A
B
1
2
D
等腰三角形的性质:
定理2:等腰三角形顶角的平分线垂直平分底边。
(等腰三角形顶角的平分线,底边上的
中线,底边上的高
“三线合一”)
符号语言表示:
∵AB=AC,∠BAD=∠CAD
∴AD⊥BC,BD=CD
如图在△ABC中,点
D在BC上
1、∵
AB
=AC,
AD
⊥
BC
∴∠1=∠__
,BD=
__
2、∵
AB
=AC,
BD=CD
∴
__
⊥
__
,
∠__
=
∠2
。
2
CD
AD
BC
1
建筑工人在盖房子时,用一块等腰三
角板放在梁上,从顶点系一重物,如果系
重物的绳子正好经过三角板底边中点,就
说房梁是水平的,你知道其中反映了什么
数学原理?
应用新知:
巩固新知:
1.填空
(1)等腰直角三角形的每一个锐角的度数是___;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是_____;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的顶角等于___________。
45°
100°
80
°或20°
例1
已知:如图,在△ABC中,AB=AC,∠BAC=
120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数。
A
B
D
E
C
同理∠2=∠C=
30°
∴∠DAE=∠BAC-(∠1+∠2)
=
120°-
(30°+
30°)
=
60°
解:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C=
×(180°-
120°)
=
30°
又∵BD=AD
(已知)
∴∠1=∠B=
30°
(等边对等角)
2
1
—
例题讲解
1
2
A
B
D
E
C
2
1
解:
∵
∠BAC=
120°
∴∠B+
∠C=180
°-
∠BAC
=60
°
∵
AD=BD
∴∠B=∠1(等边对等角)
同理:
∠C=
∠2
∠1+
∠2=
∠B+
∠C=60
°
∴∠DAE=∠BAC-(∠1+∠2)
=
120°-60
°
=60
°
如图,AD是等腰三角形ABC的顶角平分线,E是AB上的点,请在AD上找一点P,使PE+PB的值最小.
B
C
E
A
●
D
思考
P
●
┐
课堂小结
等腰三角形的性质
等腰三角形
三线合一
1、求有关等腰三角形的问题,作
顶角平分线、底边中线,底边的
高是常用的辅助线;
2、熟练掌握求解等腰三角形的顶
角、底角的度数;
3、掌握等腰三角形三线合一的
应用。
等边对等角
这节课我们学习了什么?
谈谈你的收获和疑惑!
作
业:
习题
15.3
P139
1,2,3,5
