人教版高中物理选修3-4 11.2简谐运动的描述(共53张PPT)
文档属性
| 名称 | 人教版高中物理选修3-4 11.2简谐运动的描述(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 49.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览











文档简介
(共53张PPT)
简谐运动的描述
教学目标
理解振幅、周期和频率,了解相位。?
能用公式描述简谐运动。?
简谐运动的振幅、周期和频率的概念。?
相位的物理意义。?
振幅和位移的联系和区别、周期和频率的联系和区别。?
对全振动概念的理解,对振动的快慢和振动物体运动的快
慢的理解。?
相位的物理意义。?
教学难点
教学重点
前情回顾
什么是简谐运动?
如果质点的位移与时间的关系遵从正弦函数的规律,即它
的振动图像(x-t图像)是一条正弦曲线,这样的振动叫做
简谐运动。
简谐运动的图像是怎样的?
是一条正弦曲线
以下两个振子的运动位移有何不同?
下面振动的最大位移比上面的要大
掌握简谐运动振幅的物理意义。?
掌握简谐运动周期、频率的物理意义。?
掌握简谐运动中相位的物理意义。?
描述简谐运动的物理量
描述简谐运动的物理量——振幅
定义:振动物体离开平衡位置的最大距离,叫做振动的振幅,
单位是m。
振幅是描述振动强弱的物理量,常用字母A表示。
静止位置:即平衡位置
振子振动范围的大小,就是振幅的两倍2A。?
振幅
振幅
描述简谐运动的物理量——振幅
如图,在竖直弹簧振子的简谐运动中
O点为平衡位置,小球运动的最高点
和最低点分别是M点和M’点
描述简谐运动的物理量——振幅
区分振幅和位移
对于一个给定的振动:
①振子的位移是偏离平衡位
置的距离,故时刻在变化;
但振幅是不变的。
②位移是矢量,振幅是标量,
它等于最大位移的数值。
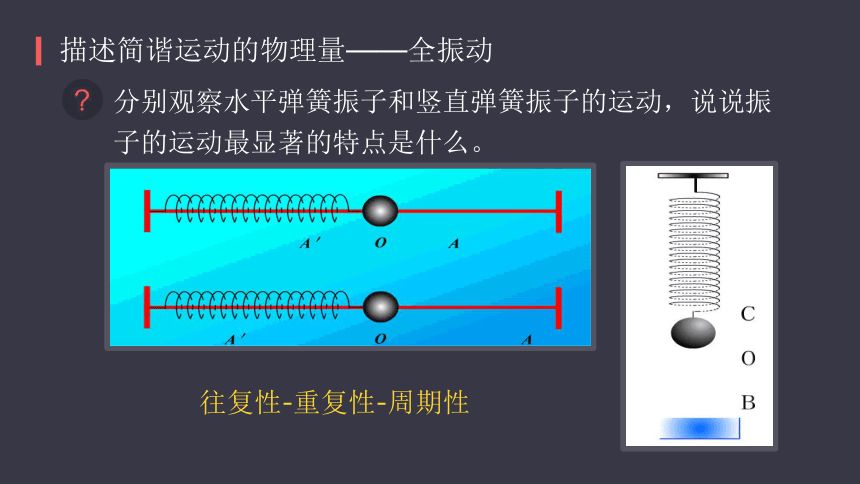
描述简谐运动的物理量——全振动
分别观察水平弹簧振子和竖直弹簧振子的运动,说说振
子的运动最显著的特点是什么。
往复性-重复性-周期性
描述简谐运动的物理量——全振动
振子在AA’之间振动,O为平衡位置。如果从A点开始运动,
经O点运动到A’点,再经过O点回到A点,就说它完成了一
次全振动,此后振子只是重复这种运动。
①从O→A→O→A’→O也是一次全振动
②从B→A→O→A’→O→B也是一次全振动
A?
?
?
?
?
?
?
?
?
?
?
?
?
?
?O?
?
?
?
?
?
?
?
?
?
?
?
?
?
A’
B
振子在AA’之间振动,O为平衡位置。如果从A点开始运动,
经O点运动到A’点,再经过O点回到A点,就说它完成了一
次全振动,此后振子只是重复这种运动。
一次全振动的特点:振动路程为振幅的4倍
A?
?
?
?
?
?
?
?
?
?
?
?
?
?
?O?
?
?
?
?
?
?
?
?
?
?
?
?
?
A’
B
描述简谐运动的物理量——全振动
描述简谐运动的物理量——全振动
如图,在竖直弹簧振子的简谐运动中
O→M→O→M’→O是完整的一次全振动
还有哪些过程是完整的一次全振动
M→O→M’→
O→M
M’→
O→
M→O→
M’
描述简谐运动的物理量——全振动
一个完整的全振动过程,振子的速度有什么显著的特点?
在一次全振动过程中,一定是振子连续两次以相同速度
通过同一点所经历的过程。
描述简谐运动的物理量——全振动
试指出一个完整的全振动过程在振动图中对应哪段曲线?
描述简谐运动的物理量——周期和频率
以下两个振子的运动快慢有何不同?
完成一个全振动所经历的时间相同
描述简谐运动的物理量——周期和频率
周期T:做简谐运动的物体完成一次全振动所需的时间,
单位:s。
经过一个周期,振动物体的振动状态完全恢复
频率f:单位时间内完成的全振动的次数,单位:Hz。
周期和频率之间的关系:
f=1/T
物理意义:描述振动快慢的物理量
周期越小,频率越大,运动越快。
描述简谐运动的物理量——周期和频率
在简谐运动的振动图中,一个周期对应的过程。?
从经过平衡位置到下一次
以相同速度经过平衡位置
从到达最大位移到下一次
以相同速度到达最大位移
从任意位置到下一次
以相同速度到达该位置
描述简谐运动的物理量——周期和频率
如图所示,为一个竖直方向振动的弹簧振子,O为静止时
的位置,当把振子拉到下方的B位置后,从静止释放,振
子将在AB之间做简谐运动,给你一个秒表,怎样测出振
子的振动周期T?
为了减小测量误差,采用累积法测振子的振
动周期T,即用秒表测出发生n次全振动所
用的总时间t,可得周期为
T=t/n
影响简谐运动周期大小的因素
周期和频率都反映弹簧振子振动的快慢,那么它们与哪些因素
有关呢?
猜想:
振幅、劲度系数、质量
控制变量法
影响简谐运动周期大小的因素
探究:弹簧振子周期的影响因素——振幅
弹簧振子的周
期与振幅无关。?
影响简谐运动周期大小的因素
探究:弹簧振子周期的影响因素——劲度系数
其他条件相同时,
弹簧劲度系数越大,
弹簧振子的周期越
小。
影响简谐运动周期大小的因素
探究:弹簧振子周期的影响因素——振子质量
其他条件相同时,
弹簧的质量越大,
弹簧振子的周期
越大。
影响简谐运动周期大小的因素
总结
①弹簧振子的振子质量越大,弹簧的劲度系数越小,其
周期越大;
②弹簧振子的周期与振幅无关
弹簧振子的周期由振动系统本身的质量和劲度系数决定,而
与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
影响简谐运动周期大小的因素
周期由系统自身的性质决定,与振动的振幅无关。
声音响度——振动幅度
声音音调——振动频率
大量实验结果表明:
简谐运动周期的公式
弹簧振子做简谐运动的周期与振幅无关,只由振子质量和弹簧的劲度系数决定。
简谐运动周期公式的理解
对公式的理解
(以竖直弹簧振子为例)
k一定时,T与m的关系
质量大的加速
度小
通过相同距离所用的时间较长
F=kx
F=kx=ma
劲度系数大的
加速度大
通过相同距离所用的时间较短
简谐运动周期公式的理解
对公式的理解
(以竖直弹簧振子为例)
F=kx
kx=ma
m一定时,T与k的关系
简谐运动周期公式的理解
对公式的理解
(以竖直弹簧振子为例)
F=kx
kx=ma
T与A无关
振幅大的虽然
运动的距离较长
但其加速度也较大
简谐运动周期和振幅的联系
简谐运动中,周期和振幅有什么联系吗?
1T内,物体通过的路程为______?
4A
T/2内,物体通过的路程为2A?
简谐运动周期和振幅的联系
T/2内,物体通过的路程一定为2A
T/4内,物体通过的路程为A?
简谐运动周期和振幅的联系
不一定
并列悬挂两个小球,悬线长度相同。
描述简谐运动的物理量——相位
把它们拉起同样的角度后同时放开。
振幅、周期都相同,并且振动同步
如果先放第一个小球,后放第二
个小球,此时它们的运动步调还
一致吗?
不一致
相位:描述振动物体所处的状态
描述简谐运动的物理量——相位
A、B同相位
A、B反相位
A相位落后于B
月相
随着月亮每天在星空中自西向东移动,在地球上看,它的形状
从圆到缺,又从缺到圆周期性地变化着,周期为29.5天,这就
是月亮位相的变化,叫做月相。
随着月亮相对于地球和太阳的位置变化,使它被太阳照亮的一面有时朝向地球,有时背向地球;
朝向地球的月亮部分有时大一些,有时小一些,这样就出现了不同的月相。
人有悲欢离合,
月有阴晴圆缺
月相
上弦
朔
下弦
望
月相
朔——当月球运行到太阳与地球之间,被太阳
照亮的半球背对着地球,此时地球上的人们就
看不到月球,这一天称为“新月”,也叫“朔
日”,即农历初一。
上弦——随后,月球自西向东逐渐远离太阳,
到了农历初七、八,半个亮区对着地球,人们
可以看到半个月亮(凸面向西),这一月相叫
“上弦月”。
出现在黄昏
月相
望——当月球运行到地球的背日方向,即农
历十五、十六、十七,月球的亮区全部对着
地球,我们能看到一轮圆月,这一月相称为
“满月”,也叫“望”。
下弦——满月过后,月球逐渐向太阳靠拢,
亮区西侧开始亏缺,到农历二十二、二十三,
又能看到半个月亮(凸面向东),这一月相
叫做“下弦月”。
出现在清晨
简谐运动的图像是一个正弦曲线,那么你能写出它的表达式吗?
会运用数学表达式来表示简谐运动。?
能根据简谐运动的表示式获取简谐运动的各物理量信息。?
简谐运动的表达式
简谐运动的表达式
简谐运动的图像
简谐运动的表达式:
简谐运动完成一次全振动
振动图象:正弦曲线
A表示简谐运动的振幅
简谐运动的表达式
简谐运动的表达式
而
简谐运动的表达式
简谐运动的表达式
一个物体运动时其相位变化多少就意味着完成了一次全振动?
相位每增加2π就意味着发生了一次全振动
简谐运动的表达式
两个振动频率相同的简谐运动的相位差
对频率相同的两
个简谐运动有确
定的相位差
简谐运动的表达式
意味着乙总是比甲滞后1/4个周期或1/4次全振动
简谐运动的表达式
相位
振幅
圆频率
初相位
问题与练习
问题与练习
如图是两个简谐运动的振动图象,它们的相位差是多少?
问题与练习
?
依题可分别写出甲、乙两个运动中x
随t变化的关系式
问题与练习
如图为A、B两个简谐运动的位移——时间图象。请根据图象写
出这两个简谐运动的位移随时间变化的关系式。
总结
简谐运动
的描述
描述简谐运
动的物理量
简谐运动的表达式
振幅A:振动物体离开平衡位置的最大距离
周期T:完成一次全振动所需要的时间
频率f:单位时间内完成全振动的次数
相位:周期性运动的物体在各个时刻所处的不
同的状态
相位差
简谐运动的描述
教学目标
理解振幅、周期和频率,了解相位。?
能用公式描述简谐运动。?
简谐运动的振幅、周期和频率的概念。?
相位的物理意义。?
振幅和位移的联系和区别、周期和频率的联系和区别。?
对全振动概念的理解,对振动的快慢和振动物体运动的快
慢的理解。?
相位的物理意义。?
教学难点
教学重点
前情回顾
什么是简谐运动?
如果质点的位移与时间的关系遵从正弦函数的规律,即它
的振动图像(x-t图像)是一条正弦曲线,这样的振动叫做
简谐运动。
简谐运动的图像是怎样的?
是一条正弦曲线
以下两个振子的运动位移有何不同?
下面振动的最大位移比上面的要大
掌握简谐运动振幅的物理意义。?
掌握简谐运动周期、频率的物理意义。?
掌握简谐运动中相位的物理意义。?
描述简谐运动的物理量
描述简谐运动的物理量——振幅
定义:振动物体离开平衡位置的最大距离,叫做振动的振幅,
单位是m。
振幅是描述振动强弱的物理量,常用字母A表示。
静止位置:即平衡位置
振子振动范围的大小,就是振幅的两倍2A。?
振幅
振幅
描述简谐运动的物理量——振幅
如图,在竖直弹簧振子的简谐运动中
O点为平衡位置,小球运动的最高点
和最低点分别是M点和M’点
描述简谐运动的物理量——振幅
区分振幅和位移
对于一个给定的振动:
①振子的位移是偏离平衡位
置的距离,故时刻在变化;
但振幅是不变的。
②位移是矢量,振幅是标量,
它等于最大位移的数值。
描述简谐运动的物理量——全振动
分别观察水平弹簧振子和竖直弹簧振子的运动,说说振
子的运动最显著的特点是什么。
往复性-重复性-周期性
描述简谐运动的物理量——全振动
振子在AA’之间振动,O为平衡位置。如果从A点开始运动,
经O点运动到A’点,再经过O点回到A点,就说它完成了一
次全振动,此后振子只是重复这种运动。
①从O→A→O→A’→O也是一次全振动
②从B→A→O→A’→O→B也是一次全振动
A?
?
?
?
?
?
?
?
?
?
?
?
?
?
?O?
?
?
?
?
?
?
?
?
?
?
?
?
?
A’
B
振子在AA’之间振动,O为平衡位置。如果从A点开始运动,
经O点运动到A’点,再经过O点回到A点,就说它完成了一
次全振动,此后振子只是重复这种运动。
一次全振动的特点:振动路程为振幅的4倍
A?
?
?
?
?
?
?
?
?
?
?
?
?
?
?O?
?
?
?
?
?
?
?
?
?
?
?
?
?
A’
B
描述简谐运动的物理量——全振动
描述简谐运动的物理量——全振动
如图,在竖直弹簧振子的简谐运动中
O→M→O→M’→O是完整的一次全振动
还有哪些过程是完整的一次全振动
M→O→M’→
O→M
M’→
O→
M→O→
M’
描述简谐运动的物理量——全振动
一个完整的全振动过程,振子的速度有什么显著的特点?
在一次全振动过程中,一定是振子连续两次以相同速度
通过同一点所经历的过程。
描述简谐运动的物理量——全振动
试指出一个完整的全振动过程在振动图中对应哪段曲线?
描述简谐运动的物理量——周期和频率
以下两个振子的运动快慢有何不同?
完成一个全振动所经历的时间相同
描述简谐运动的物理量——周期和频率
周期T:做简谐运动的物体完成一次全振动所需的时间,
单位:s。
经过一个周期,振动物体的振动状态完全恢复
频率f:单位时间内完成的全振动的次数,单位:Hz。
周期和频率之间的关系:
f=1/T
物理意义:描述振动快慢的物理量
周期越小,频率越大,运动越快。
描述简谐运动的物理量——周期和频率
在简谐运动的振动图中,一个周期对应的过程。?
从经过平衡位置到下一次
以相同速度经过平衡位置
从到达最大位移到下一次
以相同速度到达最大位移
从任意位置到下一次
以相同速度到达该位置
描述简谐运动的物理量——周期和频率
如图所示,为一个竖直方向振动的弹簧振子,O为静止时
的位置,当把振子拉到下方的B位置后,从静止释放,振
子将在AB之间做简谐运动,给你一个秒表,怎样测出振
子的振动周期T?
为了减小测量误差,采用累积法测振子的振
动周期T,即用秒表测出发生n次全振动所
用的总时间t,可得周期为
T=t/n
影响简谐运动周期大小的因素
周期和频率都反映弹簧振子振动的快慢,那么它们与哪些因素
有关呢?
猜想:
振幅、劲度系数、质量
控制变量法
影响简谐运动周期大小的因素
探究:弹簧振子周期的影响因素——振幅
弹簧振子的周
期与振幅无关。?
影响简谐运动周期大小的因素
探究:弹簧振子周期的影响因素——劲度系数
其他条件相同时,
弹簧劲度系数越大,
弹簧振子的周期越
小。
影响简谐运动周期大小的因素
探究:弹簧振子周期的影响因素——振子质量
其他条件相同时,
弹簧的质量越大,
弹簧振子的周期
越大。
影响简谐运动周期大小的因素
总结
①弹簧振子的振子质量越大,弹簧的劲度系数越小,其
周期越大;
②弹簧振子的周期与振幅无关
弹簧振子的周期由振动系统本身的质量和劲度系数决定,而
与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
影响简谐运动周期大小的因素
周期由系统自身的性质决定,与振动的振幅无关。
声音响度——振动幅度
声音音调——振动频率
大量实验结果表明:
简谐运动周期的公式
弹簧振子做简谐运动的周期与振幅无关,只由振子质量和弹簧的劲度系数决定。
简谐运动周期公式的理解
对公式的理解
(以竖直弹簧振子为例)
k一定时,T与m的关系
质量大的加速
度小
通过相同距离所用的时间较长
F=kx
F=kx=ma
劲度系数大的
加速度大
通过相同距离所用的时间较短
简谐运动周期公式的理解
对公式的理解
(以竖直弹簧振子为例)
F=kx
kx=ma
m一定时,T与k的关系
简谐运动周期公式的理解
对公式的理解
(以竖直弹簧振子为例)
F=kx
kx=ma
T与A无关
振幅大的虽然
运动的距离较长
但其加速度也较大
简谐运动周期和振幅的联系
简谐运动中,周期和振幅有什么联系吗?
1T内,物体通过的路程为______?
4A
T/2内,物体通过的路程为2A?
简谐运动周期和振幅的联系
T/2内,物体通过的路程一定为2A
T/4内,物体通过的路程为A?
简谐运动周期和振幅的联系
不一定
并列悬挂两个小球,悬线长度相同。
描述简谐运动的物理量——相位
把它们拉起同样的角度后同时放开。
振幅、周期都相同,并且振动同步
如果先放第一个小球,后放第二
个小球,此时它们的运动步调还
一致吗?
不一致
相位:描述振动物体所处的状态
描述简谐运动的物理量——相位
A、B同相位
A、B反相位
A相位落后于B
月相
随着月亮每天在星空中自西向东移动,在地球上看,它的形状
从圆到缺,又从缺到圆周期性地变化着,周期为29.5天,这就
是月亮位相的变化,叫做月相。
随着月亮相对于地球和太阳的位置变化,使它被太阳照亮的一面有时朝向地球,有时背向地球;
朝向地球的月亮部分有时大一些,有时小一些,这样就出现了不同的月相。
人有悲欢离合,
月有阴晴圆缺
月相
上弦
朔
下弦
望
月相
朔——当月球运行到太阳与地球之间,被太阳
照亮的半球背对着地球,此时地球上的人们就
看不到月球,这一天称为“新月”,也叫“朔
日”,即农历初一。
上弦——随后,月球自西向东逐渐远离太阳,
到了农历初七、八,半个亮区对着地球,人们
可以看到半个月亮(凸面向西),这一月相叫
“上弦月”。
出现在黄昏
月相
望——当月球运行到地球的背日方向,即农
历十五、十六、十七,月球的亮区全部对着
地球,我们能看到一轮圆月,这一月相称为
“满月”,也叫“望”。
下弦——满月过后,月球逐渐向太阳靠拢,
亮区西侧开始亏缺,到农历二十二、二十三,
又能看到半个月亮(凸面向东),这一月相
叫做“下弦月”。
出现在清晨
简谐运动的图像是一个正弦曲线,那么你能写出它的表达式吗?
会运用数学表达式来表示简谐运动。?
能根据简谐运动的表示式获取简谐运动的各物理量信息。?
简谐运动的表达式
简谐运动的表达式
简谐运动的图像
简谐运动的表达式:
简谐运动完成一次全振动
振动图象:正弦曲线
A表示简谐运动的振幅
简谐运动的表达式
简谐运动的表达式
而
简谐运动的表达式
简谐运动的表达式
一个物体运动时其相位变化多少就意味着完成了一次全振动?
相位每增加2π就意味着发生了一次全振动
简谐运动的表达式
两个振动频率相同的简谐运动的相位差
对频率相同的两
个简谐运动有确
定的相位差
简谐运动的表达式
意味着乙总是比甲滞后1/4个周期或1/4次全振动
简谐运动的表达式
相位
振幅
圆频率
初相位
问题与练习
问题与练习
如图是两个简谐运动的振动图象,它们的相位差是多少?
问题与练习
?
依题可分别写出甲、乙两个运动中x
随t变化的关系式
问题与练习
如图为A、B两个简谐运动的位移——时间图象。请根据图象写
出这两个简谐运动的位移随时间变化的关系式。
总结
简谐运动
的描述
描述简谐运
动的物理量
简谐运动的表达式
振幅A:振动物体离开平衡位置的最大距离
周期T:完成一次全振动所需要的时间
频率f:单位时间内完成全振动的次数
相位:周期性运动的物体在各个时刻所处的不
同的状态
相位差
