人教版高中物理选修3-4 11.3简谐运动的回复力和能量(共39张PPT)
文档属性
| 名称 | 人教版高中物理选修3-4 11.3简谐运动的回复力和能量(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 36.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览










文档简介
(共39张PPT)
简谐运动的回复力和能量
教学目标
理解回复力的概念
会用动力学的方法,分析简谐运动中位移、速度、回复力和加速度的变化规律
会用能量守恒的观点,分析水平弹簧振子中动能、势能、总能量的变化规律
教学重点
回复力的来源、特点
简谐运动的证明,简谐运动的能量特点
教学难点
回复力的特点
简谐运动的动力学分析及能量分析
什么是机械振动?机械振动具有什么特点?
简谐运动的表达式是什么?其振动图象具有什么特点?
简谐运动的表达式:?
前情提要
机械振动:物体在平衡位置附近所做的往复运动特点:①对称性;②周期性
其图象是正弦曲线
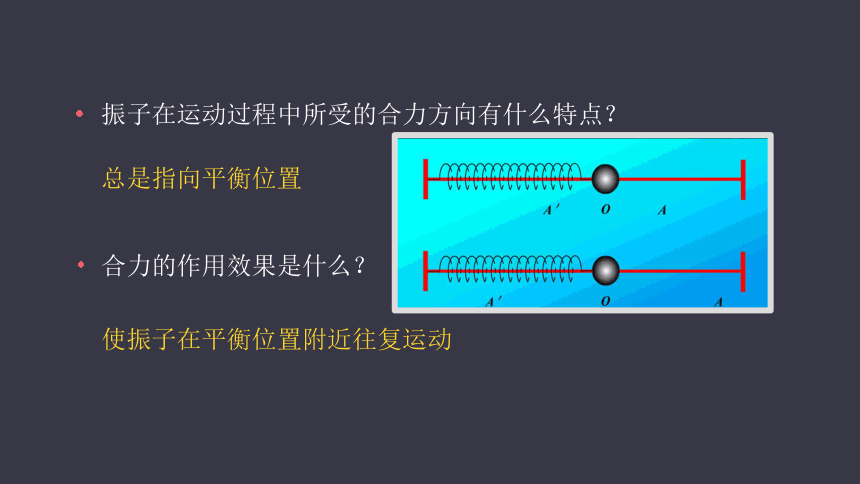
振子在运动过程中所受的合力方向有什么特点?
总是指向平衡位置
合力的作用效果是什么?
使振子在平衡位置附近往复运动
掌握简谐运动中的回复力方向
掌握判断简谐运动的回复力大小的方法
能根据回复力判断运动是否为简谐运动
简谐运动的回复力
简谐运动的回复力
定义:振动物体受到的总是指向平衡位置的力叫做回复力
方向:总是指向平衡位置
效果:总是把物体拉回到平衡位置
回复力是按力的作用效果命名的(类似向心力)
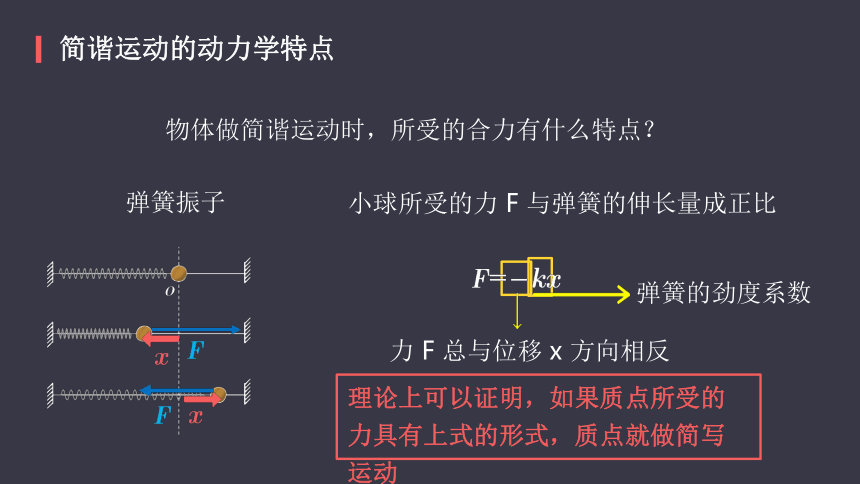
简谐运动的动力学特点
物体做简谐运动时,所受的合力有什么特点?
小球所受的力
F
与弹簧的伸长量成正比
弹簧的劲度系数
力
F
总与位移
x
方向相反
理论上可以证明,如果质点所受的力具有上式的形式,质点就做简写运动
弹簧振子
简谐运动的动力学特点
简谐运动的动力学特点
k
是比例系数,其值由振动系统决定,与振幅无关
“-”
表示回复力方向始终与位移方向相反
回复力满足
?
?
?
?
?
?
?的运动就是简谐运动
注意:
对一般的简谐运动,由于回复力不一定是弹簧的弹力,所以k不一定是劲度系数,而是回复力与位移的比例系数。
如果质点所受的回复力与它偏离平衡位置的位移大小成正比,并且总是指向平衡位置
(即与位移方向相反),质点的运动就是简谐运动
简谐运动的加速度
做简谐运动的物体,在运动的过程中,加速度是如何变化的?
简谐运动的加速度
a
总与位移的大小成正比,方向与位移的方向相反
a
与
F
的变化规律相同
简谐运动是一种变加速的往复运动
简谐运动的运动学特点
简谐运动的运动学特点
简谐运动的回复力随时间会如何变化?
回复力大小随时间按正弦曲线变化。
简谐运动的证明
简谐运动的动力学特征
简谐运动的运动学特征
常用两式来证明某个振动为简谐运动
需证明回复力与位移的大小关系;
需证明回复力与位移的方向关系;
证明振动的图象为正弦图象即可
振动图像是正弦曲线
简谐运动的证明
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
判断物体是否做简谐运动的方法:
运动学法:振动图像;
动力学法:
简谐运动的证明
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
证明:
平衡状态时有:
当向下拉动x长度时弹簧所受的合外力为
(符合简谐运动的公式)
简谐运动的证明
斜面上小球——弹簧振动系统
一个振动,如果回复力与偏离平衡位置的位移成正比而且方向与位移相反,就能判定它是简谐运动。请你据此证明:把下图中倾角为θ
的光滑斜面上的小球沿斜面拉下一段距离,然后松开,小球的运动是简谐运动。
小球静止时受到重力、斜面的支持力和弹簧的拉力三个力的作用。平衡时弹簧伸长了
?
?
,则
弹簧拉长后,设离开平衡位置的位移为
x,规定
x
方向为正方向,则弹簧的拉力
小球沿斜面方向受的合力即为小球受的回复力
这个力与偏离平衡位置的位移成正比且方向相反,因此小球的运动是简谐运动
简谐运动的证明
某人想判定以下振动是不是简谐运动,请你陈述求证的思路(可以不做定量证明)
1.
粗细均匀的一条木块,下端绕几圈铁丝,竖直浮在较大的筒中(如图)。把木筷往上提起一段距离后放手,木筷就在水中上下振动;
2.
光滑圆弧面上有一个小球,把它从最低点移开一小段距离,放手后,小球以最低点为平衡位置左右振动(如图)。
均匀木筷在水中的上下振动
圆弧面上小球的左右振动
(1)如果不考虑水的粘滞阻力,木筷受到重力和水的浮力,重力恒定不变,浮力与排开水的体积成正比,木筷静止时的位置看做平衡位置。以平衡位置为坐标原点,如果木筷所受合力与其偏离平衡位置的位移成正比,且方向相反,则可判定木筷做简谐运动。
(2)小球受到重力和圆弧面的支持力。重力恒定不变,支持力始终与运动方向垂直。如果重力沿圆弧面切线方向的分力与其偏离平衡位置的位移成正比,且方向相反,则可判定木筷做简谐运动
简谐运动的证明
物体沿直线振动时回复力就是合力;
沿圆弧振动时回复力是合力在圆弧切线方向上的分力。
物体做简谐运动到平衡位置时,回复力为零,但合力可能不为零
简谐运动回复力的来源
回复力的来源:
物体在振动方向上的合力
回复力由弹簧的弹力提供
回复力由弹簧的弹力与重力的合力提供
m随M
一起振动,
m的回复力是静摩擦力。
可以是一个力单独提供,也可由几个力的合力提供,或由某个力的分力提供
简谐运动中力及运动的分析
振子位置
物理量
位移
速度
大小
方向
大小
A'
A'→O
O
O→A
A
A→O
O
O→A'
最大
最大
向左
向左
减小
0
-
增大
0
-
增大
向右
减小
0
-
最大
向右
减小
向右?
增大
0
-
最大
增大
向左
减小
变化规律
方向
向右
向右
向右
向左
向左
向左
简谐运动中力及运动的分析
振子位置
物理量
变化规律
A'
A'→O
O
O→A
A
A→O
O
O→A'
回复力
?
?
F
加速度
?
?
?a
大小
方向
大小
最大
最大
减小
减小
0
-
0
-
增大
增大
最大
最大
减小
减小
0
-
0
-
增大
增大
方向
向右
向右
向右
向右
向右
向右
向左
向左
向左
向左
向左
向左
简谐运动中力及运动的分析
振子位置
物理量
变化规律
位移
回复力
?
?
?F
加速度
?
?
?a
速度
大小
方向
大小
大小
方向
大小
A'
A'→O
O
O→A
A
A→O
O
O→A'
最大
向左
向左
减小
0
-
增大
向右
最大
向右
减小
向右?
0
-
增大
向左
最大
0
-
增大
减小
0
-
增大
最大
减小
最大
最大
减小
减小
0
-
0
-
增大
增大
最大
最大
减小
减小
0
-
0
-
增大
增大
方向
方向
向右
向右
向右
向右
向右
向右
向右
向右
向右
向左
向左
向左
向左
向左
向左
向左
向左
向左
简谐运动中力及运动的分析
简谐运动的加速度大小和方向都随时间做周期性的变化,所以简谐运动是变加速运动。
①当物体从最大位移处向平衡位置运动时,由于v与a的方向一致,物体做加速度越来越小的加速运动。
②当物体从平衡位置向最大位移处运动时,由于v与a的方向相反,物体做加速度越来越大的减速运动。
简谐运动中力及运动的分析
简谐运动图象表示某个振动物体相对平衡位置的位移随时间变化的规律。
正弦或余弦曲线
从图线可以知道振幅周期(频率)、任一时刻物体对平衡位置的位移,还可以说明振动物体的速度、加速度大小和方向随时间变化的情况。
在简谐运动过程中,振子能量变化情况如何?
理解并掌握求解简谐运动的弹性势能
掌握简谐运动的动能与弹性势能的转化规律
简谐运动的能量
简谐运动的能量
弹簧振子的运动与能量的关系
速度与动能:
速度增加,动能也增加
弹簧形变量与势能:
弹簧形变量在变化,因而势能也在变化
水平弹簧振子在A、B之间往复运动
弹性势能最小的位置是________
A、B
弹性势能最大的位置是________
O
简谐运动的能量
在一个周期内,弹簧振子的能量是如何变化的?
从A→O的过程中,动能______,势能______;
从O→B,动能______,势能______;
从B→O,动能______,势能______;
从O→A,动能______,势能______;
在平衡位置,动能______,势能______;
在最大位移处,动能______,势能______;
在一个周期内动能和势能大小做___次周期性变化
增大
减小
最大
为零
两
增大
减小
增大
减小
最大
为零
增大
减小
简谐运动的能量
简谐运动中振子的能量变化情况分析
A'
A'→O
O
O→A
A
A→O
O
O→A'
动能
势能
0
最大
增大
减小
0
最大
增大
减小
0
最大
增大
减小
0
最大
增大
减小
简谐运动的能量
简谐运动的机械能大小跟什么因素有关?振幅还是频率?
简谐运动的机械能由振幅决定。
振幅越大,振动的能量越大。
不考虑阻力,
水平弹簧振子振动过程中只有______做功,
在任意时刻的动能与势能之和_____,
即机械能守恒
弹力
不变
只要没有能量损耗,简谐运动的振幅保持不变,它将永不停息地振动下去,因此简谐运动又称为等幅振动。
简谐运动的能量
简谐运动中振子的能量变化情况分析
A'
A'→O
O
O→A
A
A→O
O
O→A'
最大
减小
0
增大
增大
减小
最大
减小
增大
最大
增大
减小
动能
势能
总能
最大
0
不变
0
0
简谐运动的能量
简谐运动中动能和势能相互转换,总的机械能保持守恒。
在平衡位置动能最大,势能最小。
能量随空间变化
能量随时间变化
简谐运动的能量
动能和势能是互余的
简谐运动的能量
不同的弹簧,做相同振幅的水平简谐运动,其能量相同吗?水平弹簧振子的简谐运动中,能量除了与振幅有关外,还有什么因素有关?
简谐运动的能量由劲度系数和振幅决定。
劲度系数越大,振幅越大,振动的能量越大
简谐运动的两个特殊位置
最大位移处
x、F、a、Ep最大,v=0,Ek=0
平衡位置处
x=0、F=0、a=0、Ep最小,v,Ek最大
问题与练习
平衡位置在A、B之间,距A点4cm,距B点6cm
问题与练习
如图为某物体做简谐运动的图象,在所画曲线的范围内回答下列问题。(1)哪些时刻物体的回复力与0.4s时刻的回复力相同?
(2)哪些时刻物体的速度与0.4s时刻的速度相同?
(3)哪些时刻的动能与0.4s时刻的动能相同?
(4)哪些时间的加速度在减小?(5)哪些时间的势能在增大?
(1)0.6s、1.2s、1.4s
(2)0.2s、1.0s、1.2s
(3)0、0.2s、0.6s、0.8s、1.0s、1.2s、1.4s
(4)0.1~0.3s、0.5~0.7s、0.9~1.1s、1.3~1.5s
(5)0~0.1s、0.3~0.5s、0.7s~0.9s、1.1~1.3s
简谐运动的对称性
时间的对称性:
振动质点来回通过相同两点时间相等
质点经过关于平衡位置对称的两端距离时间相等
经过半周期后质点一定位于对称位置
简谐运动的对称性
位移和加速度的对称性
同一位置,位移和加速度相同
对称位置加速度大小相等、方向相反
位移大小相等、方向相反
速度的对称性
同一位置或对称位置,速度大小相等,方向未必相同
总结
简谐运动
回复力
特点
能量
回复力:振动物体受到的总是指向平衡位置的力。
是物体在振动方向上的合外力。
动力学特点:
运动学特点:
简谐运动中动能和势能在发生相互转化,但机械能的总量保持不变,即机械能守恒。
简谐运动的回复力和能量
教学目标
理解回复力的概念
会用动力学的方法,分析简谐运动中位移、速度、回复力和加速度的变化规律
会用能量守恒的观点,分析水平弹簧振子中动能、势能、总能量的变化规律
教学重点
回复力的来源、特点
简谐运动的证明,简谐运动的能量特点
教学难点
回复力的特点
简谐运动的动力学分析及能量分析
什么是机械振动?机械振动具有什么特点?
简谐运动的表达式是什么?其振动图象具有什么特点?
简谐运动的表达式:?
前情提要
机械振动:物体在平衡位置附近所做的往复运动特点:①对称性;②周期性
其图象是正弦曲线
振子在运动过程中所受的合力方向有什么特点?
总是指向平衡位置
合力的作用效果是什么?
使振子在平衡位置附近往复运动
掌握简谐运动中的回复力方向
掌握判断简谐运动的回复力大小的方法
能根据回复力判断运动是否为简谐运动
简谐运动的回复力
简谐运动的回复力
定义:振动物体受到的总是指向平衡位置的力叫做回复力
方向:总是指向平衡位置
效果:总是把物体拉回到平衡位置
回复力是按力的作用效果命名的(类似向心力)
简谐运动的动力学特点
物体做简谐运动时,所受的合力有什么特点?
小球所受的力
F
与弹簧的伸长量成正比
弹簧的劲度系数
力
F
总与位移
x
方向相反
理论上可以证明,如果质点所受的力具有上式的形式,质点就做简写运动
弹簧振子
简谐运动的动力学特点
简谐运动的动力学特点
k
是比例系数,其值由振动系统决定,与振幅无关
“-”
表示回复力方向始终与位移方向相反
回复力满足
?
?
?
?
?
?
?的运动就是简谐运动
注意:
对一般的简谐运动,由于回复力不一定是弹簧的弹力,所以k不一定是劲度系数,而是回复力与位移的比例系数。
如果质点所受的回复力与它偏离平衡位置的位移大小成正比,并且总是指向平衡位置
(即与位移方向相反),质点的运动就是简谐运动
简谐运动的加速度
做简谐运动的物体,在运动的过程中,加速度是如何变化的?
简谐运动的加速度
a
总与位移的大小成正比,方向与位移的方向相反
a
与
F
的变化规律相同
简谐运动是一种变加速的往复运动
简谐运动的运动学特点
简谐运动的运动学特点
简谐运动的回复力随时间会如何变化?
回复力大小随时间按正弦曲线变化。
简谐运动的证明
简谐运动的动力学特征
简谐运动的运动学特征
常用两式来证明某个振动为简谐运动
需证明回复力与位移的大小关系;
需证明回复力与位移的方向关系;
证明振动的图象为正弦图象即可
振动图像是正弦曲线
简谐运动的证明
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
判断物体是否做简谐运动的方法:
运动学法:振动图像;
动力学法:
简谐运动的证明
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
证明:
平衡状态时有:
当向下拉动x长度时弹簧所受的合外力为
(符合简谐运动的公式)
简谐运动的证明
斜面上小球——弹簧振动系统
一个振动,如果回复力与偏离平衡位置的位移成正比而且方向与位移相反,就能判定它是简谐运动。请你据此证明:把下图中倾角为θ
的光滑斜面上的小球沿斜面拉下一段距离,然后松开,小球的运动是简谐运动。
小球静止时受到重力、斜面的支持力和弹簧的拉力三个力的作用。平衡时弹簧伸长了
?
?
,则
弹簧拉长后,设离开平衡位置的位移为
x,规定
x
方向为正方向,则弹簧的拉力
小球沿斜面方向受的合力即为小球受的回复力
这个力与偏离平衡位置的位移成正比且方向相反,因此小球的运动是简谐运动
简谐运动的证明
某人想判定以下振动是不是简谐运动,请你陈述求证的思路(可以不做定量证明)
1.
粗细均匀的一条木块,下端绕几圈铁丝,竖直浮在较大的筒中(如图)。把木筷往上提起一段距离后放手,木筷就在水中上下振动;
2.
光滑圆弧面上有一个小球,把它从最低点移开一小段距离,放手后,小球以最低点为平衡位置左右振动(如图)。
均匀木筷在水中的上下振动
圆弧面上小球的左右振动
(1)如果不考虑水的粘滞阻力,木筷受到重力和水的浮力,重力恒定不变,浮力与排开水的体积成正比,木筷静止时的位置看做平衡位置。以平衡位置为坐标原点,如果木筷所受合力与其偏离平衡位置的位移成正比,且方向相反,则可判定木筷做简谐运动。
(2)小球受到重力和圆弧面的支持力。重力恒定不变,支持力始终与运动方向垂直。如果重力沿圆弧面切线方向的分力与其偏离平衡位置的位移成正比,且方向相反,则可判定木筷做简谐运动
简谐运动的证明
物体沿直线振动时回复力就是合力;
沿圆弧振动时回复力是合力在圆弧切线方向上的分力。
物体做简谐运动到平衡位置时,回复力为零,但合力可能不为零
简谐运动回复力的来源
回复力的来源:
物体在振动方向上的合力
回复力由弹簧的弹力提供
回复力由弹簧的弹力与重力的合力提供
m随M
一起振动,
m的回复力是静摩擦力。
可以是一个力单独提供,也可由几个力的合力提供,或由某个力的分力提供
简谐运动中力及运动的分析
振子位置
物理量
位移
速度
大小
方向
大小
A'
A'→O
O
O→A
A
A→O
O
O→A'
最大
最大
向左
向左
减小
0
-
增大
0
-
增大
向右
减小
0
-
最大
向右
减小
向右?
增大
0
-
最大
增大
向左
减小
变化规律
方向
向右
向右
向右
向左
向左
向左
简谐运动中力及运动的分析
振子位置
物理量
变化规律
A'
A'→O
O
O→A
A
A→O
O
O→A'
回复力
?
?
F
加速度
?
?
?a
大小
方向
大小
最大
最大
减小
减小
0
-
0
-
增大
增大
最大
最大
减小
减小
0
-
0
-
增大
增大
方向
向右
向右
向右
向右
向右
向右
向左
向左
向左
向左
向左
向左
简谐运动中力及运动的分析
振子位置
物理量
变化规律
位移
回复力
?
?
?F
加速度
?
?
?a
速度
大小
方向
大小
大小
方向
大小
A'
A'→O
O
O→A
A
A→O
O
O→A'
最大
向左
向左
减小
0
-
增大
向右
最大
向右
减小
向右?
0
-
增大
向左
最大
0
-
增大
减小
0
-
增大
最大
减小
最大
最大
减小
减小
0
-
0
-
增大
增大
最大
最大
减小
减小
0
-
0
-
增大
增大
方向
方向
向右
向右
向右
向右
向右
向右
向右
向右
向右
向左
向左
向左
向左
向左
向左
向左
向左
向左
简谐运动中力及运动的分析
简谐运动的加速度大小和方向都随时间做周期性的变化,所以简谐运动是变加速运动。
①当物体从最大位移处向平衡位置运动时,由于v与a的方向一致,物体做加速度越来越小的加速运动。
②当物体从平衡位置向最大位移处运动时,由于v与a的方向相反,物体做加速度越来越大的减速运动。
简谐运动中力及运动的分析
简谐运动图象表示某个振动物体相对平衡位置的位移随时间变化的规律。
正弦或余弦曲线
从图线可以知道振幅周期(频率)、任一时刻物体对平衡位置的位移,还可以说明振动物体的速度、加速度大小和方向随时间变化的情况。
在简谐运动过程中,振子能量变化情况如何?
理解并掌握求解简谐运动的弹性势能
掌握简谐运动的动能与弹性势能的转化规律
简谐运动的能量
简谐运动的能量
弹簧振子的运动与能量的关系
速度与动能:
速度增加,动能也增加
弹簧形变量与势能:
弹簧形变量在变化,因而势能也在变化
水平弹簧振子在A、B之间往复运动
弹性势能最小的位置是________
A、B
弹性势能最大的位置是________
O
简谐运动的能量
在一个周期内,弹簧振子的能量是如何变化的?
从A→O的过程中,动能______,势能______;
从O→B,动能______,势能______;
从B→O,动能______,势能______;
从O→A,动能______,势能______;
在平衡位置,动能______,势能______;
在最大位移处,动能______,势能______;
在一个周期内动能和势能大小做___次周期性变化
增大
减小
最大
为零
两
增大
减小
增大
减小
最大
为零
增大
减小
简谐运动的能量
简谐运动中振子的能量变化情况分析
A'
A'→O
O
O→A
A
A→O
O
O→A'
动能
势能
0
最大
增大
减小
0
最大
增大
减小
0
最大
增大
减小
0
最大
增大
减小
简谐运动的能量
简谐运动的机械能大小跟什么因素有关?振幅还是频率?
简谐运动的机械能由振幅决定。
振幅越大,振动的能量越大。
不考虑阻力,
水平弹簧振子振动过程中只有______做功,
在任意时刻的动能与势能之和_____,
即机械能守恒
弹力
不变
只要没有能量损耗,简谐运动的振幅保持不变,它将永不停息地振动下去,因此简谐运动又称为等幅振动。
简谐运动的能量
简谐运动中振子的能量变化情况分析
A'
A'→O
O
O→A
A
A→O
O
O→A'
最大
减小
0
增大
增大
减小
最大
减小
增大
最大
增大
减小
动能
势能
总能
最大
0
不变
0
0
简谐运动的能量
简谐运动中动能和势能相互转换,总的机械能保持守恒。
在平衡位置动能最大,势能最小。
能量随空间变化
能量随时间变化
简谐运动的能量
动能和势能是互余的
简谐运动的能量
不同的弹簧,做相同振幅的水平简谐运动,其能量相同吗?水平弹簧振子的简谐运动中,能量除了与振幅有关外,还有什么因素有关?
简谐运动的能量由劲度系数和振幅决定。
劲度系数越大,振幅越大,振动的能量越大
简谐运动的两个特殊位置
最大位移处
x、F、a、Ep最大,v=0,Ek=0
平衡位置处
x=0、F=0、a=0、Ep最小,v,Ek最大
问题与练习
平衡位置在A、B之间,距A点4cm,距B点6cm
问题与练习
如图为某物体做简谐运动的图象,在所画曲线的范围内回答下列问题。(1)哪些时刻物体的回复力与0.4s时刻的回复力相同?
(2)哪些时刻物体的速度与0.4s时刻的速度相同?
(3)哪些时刻的动能与0.4s时刻的动能相同?
(4)哪些时间的加速度在减小?(5)哪些时间的势能在增大?
(1)0.6s、1.2s、1.4s
(2)0.2s、1.0s、1.2s
(3)0、0.2s、0.6s、0.8s、1.0s、1.2s、1.4s
(4)0.1~0.3s、0.5~0.7s、0.9~1.1s、1.3~1.5s
(5)0~0.1s、0.3~0.5s、0.7s~0.9s、1.1~1.3s
简谐运动的对称性
时间的对称性:
振动质点来回通过相同两点时间相等
质点经过关于平衡位置对称的两端距离时间相等
经过半周期后质点一定位于对称位置
简谐运动的对称性
位移和加速度的对称性
同一位置,位移和加速度相同
对称位置加速度大小相等、方向相反
位移大小相等、方向相反
速度的对称性
同一位置或对称位置,速度大小相等,方向未必相同
总结
简谐运动
回复力
特点
能量
回复力:振动物体受到的总是指向平衡位置的力。
是物体在振动方向上的合外力。
动力学特点:
运动学特点:
简谐运动中动能和势能在发生相互转化,但机械能的总量保持不变,即机械能守恒。
