人教版数学九年级上册 21.1 一元二次方程 练习课件(共26张PPT)
文档属性
| 名称 | 人教版数学九年级上册 21.1 一元二次方程 练习课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 887.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 17:11:57 | ||
图片预览





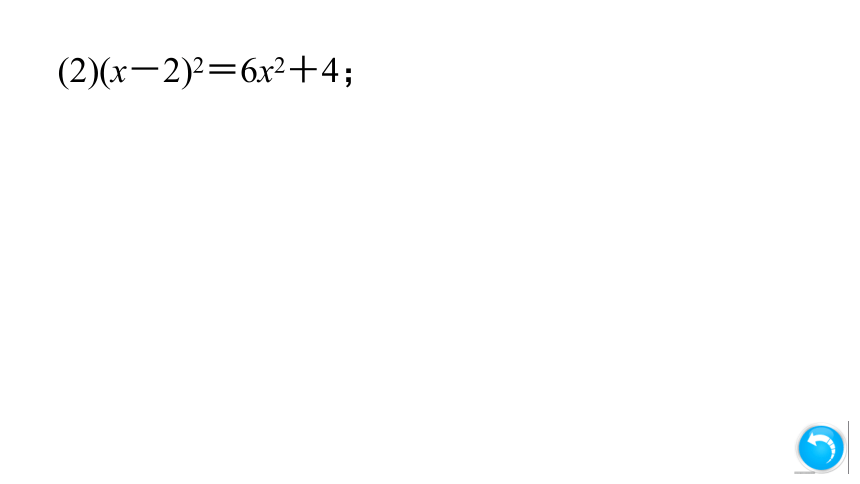

文档简介
21.1 一元二次方程
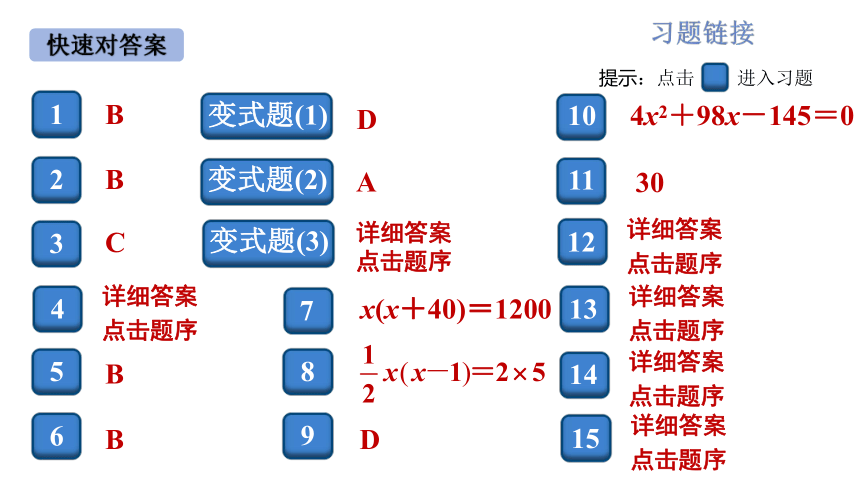
B
B
C
B
D
1
提示:点击 进入习题
快速对答案
B
A
10
9
8
7
变式题(2)
6
5
3
2
变式题(1)
11
30
D
4x2+98x-145=0
x(x+40)=1200
详细答案
点击题序
4
详细答案
点击题序
变式题(3)
详细答案
点击题序
12
详细答案
点击题序
13
详细答案
点击题序
14
详细答案
点击题序
15
知识点一 一元二次方程的概念及一般形式
1.(2019-2020·宜昌期中)下列方程中,是关于x的一元二次方程的是( B )
A.ax2+bx+c=0 B.x(x-2)=0
C. D.2x=x-1
2.若关于x的方程(a-1)x2-5x+1=0是一元二次方程,则a不能取( B )
A.0 B.1 C.-1 D.2
3.方程x(x+5)=0化成一般形式后,它的常数项是
( C )
A.-5 B.5 C.0 D.1
4.将下列一元二次方程化为一般形式,并指出其中的二次项系数、一次项系数和常数项:
(1)8x-21=x2;
解:(1)x2-8x+21=0,
二次项系数为1,
一次项系数为-8,
常数项为21.
(2)(x-2)2=6x2+4;
(2)5x2+4x=0,
二次项系数为5,
一次项系数为4,
常数项为0.
(3)2(t+2)=(t+1)2.
(3)t2-3=0,
二次项系数为1,
一次项系数为0,
常数项为-3.
知识点二 一元二次方程的解(根)
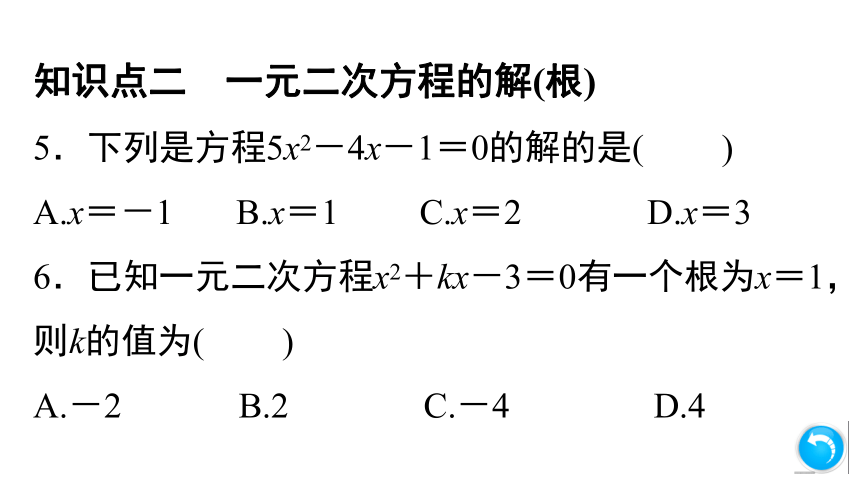
5.下列是方程5x2-4x-1=0的解的是( B )
A.x=-1 B.x=1 C.x=2 D.x=3
6.已知一元二次方程x2+kx-3=0有一个根为x=1,则k的值为( B )
A.-2 B.2 C.-4 D.4
【变式题】根据根的定义求字母的值→求代数式的值
(1)(2019·遂宁中考)已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0,则a的值为( D )
A.0 B.±1 C.1 D.-1
(2)(2019·兰州中考)已知x=1是关于x的一元二次方程x2+ax+2b=0的解,则2a+4b=( A )
A.-2 B.-3 C.-1 D.-6
(3)若2n(n≠0)是关于x的方程x2-2mx+2n=0的根,求m-n的值.
解:∵2n是方程x2-2mx+2n=0的根,
∴4n2-4mn+2n=0.
∵n≠0,
∴4n-4m+2=0.
∴4m-4n=2. ∴m-n= .
知识点三 用一元二次方程刻画实际问题中的数
量关系
7.为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为 .
x(x+40)=1200
8.某校要组织一次乒乓球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排2天,每天安排5场比赛.设比赛组织者应邀请x个队参赛,则x满足的方程为 .
9.(2019·潮南区一模)若关于x的一元二次方程(m-2)x2+5x+m2-4=0的常数项是0,则( D )
A.m=4 B.m=2
C.m=2或m=-2 D.m=-2
10.(2019·武汉期末)第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,小郑幸运获得了一张军运会吉祥物“兵兵”的照片.如图,该照片(中间的矩形)长29 cm、宽为20 cm,她想为此照片配一个四条边宽度相等的镜框(阴影部分),且镜框所占面积为照片面积的 .
为求镜框的宽度,她设镜框的宽度为x cm,依题意列方程,化成一般式为 .
4x2+98x-145=0
11.一元二次方程a(x2+1)+b(x+2)+c=0化为一般式后为6x2+10x-1=0,则以a、b为两条对角线长的菱形的面积为 .
30
12.(2019·右玉县期末)在一元二次方程x2-2ax+b=0中,若a2-b>0,则称a是该方程的中点值.
(1)方程x2-8x+3=0的中点值是 ;
4
(2)已知x2-mx+n=0的中点值是3,其中一个根是2,求mn的值.
解:∵ =3,∴m=6.
把x=2代入x2-mx+n=0,
得4-6×2+n=0,解得n=8.
∴mn=6×8=48.
13.已知方程(m-2) +(m-3)x+1=0.
(1)当m为何值时,它是一元二次方程?
解:若原方程为一元二次方程,
则 解得m=
∴所以当m为 或 时,原方程为一元二次方程.
(2)当m为何值时,它是一元一次方程?
解:若原方程为一元一次方程,
则 或 或m=0.
解得m=2,±1或0.
∴所以当m为2或±1或0时,原方程为一元一次方程.
14.已知m是方程x2-x-3=0的一个实数根,求代数式(m2-m)(m- +1)的值.
解:∵m是方程x2-x-3=0的一个实数根,
∴m2-m-3=0,即m2-m=3.
∴易知m≠0.
在m2-m-3=0两边同时除以m,得m-1- =0,
即m- =1.
∴(m2-m)(m- +1)=3×(1+1)=6.
15.【注重传统文化】《九章算术》中记载:今有户不知高、广,竿不知长短.横之不出四尺,纵之不出二尺,邪之适出.问户高、广、邪各几何?
译文是:今有门,不知其高、宽,有竿,不知其长短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.
问门高、宽、对角线的长分别是多少?若设门对角线的长为x尺,根据题意列出方程并化为一般形式.
解:如图,由题设可知对角线AB的长为x尺,则门的宽度AC长为(x-4)尺,
门的高度BC长为(x-2)尺.
根据勾股定理得(x-4)2+(x-2)2=x2,
整理得x2-12x+20=0.
B
B
C
B
D
1
提示:点击 进入习题
快速对答案
B
A
10
9
8
7
变式题(2)
6
5
3
2
变式题(1)
11
30
D
4x2+98x-145=0
x(x+40)=1200
详细答案
点击题序
4
详细答案
点击题序
变式题(3)
详细答案
点击题序
12
详细答案
点击题序
13
详细答案
点击题序
14
详细答案
点击题序
15
知识点一 一元二次方程的概念及一般形式
1.(2019-2020·宜昌期中)下列方程中,是关于x的一元二次方程的是( B )
A.ax2+bx+c=0 B.x(x-2)=0
C. D.2x=x-1
2.若关于x的方程(a-1)x2-5x+1=0是一元二次方程,则a不能取( B )
A.0 B.1 C.-1 D.2
3.方程x(x+5)=0化成一般形式后,它的常数项是
( C )
A.-5 B.5 C.0 D.1
4.将下列一元二次方程化为一般形式,并指出其中的二次项系数、一次项系数和常数项:
(1)8x-21=x2;
解:(1)x2-8x+21=0,
二次项系数为1,
一次项系数为-8,
常数项为21.
(2)(x-2)2=6x2+4;
(2)5x2+4x=0,
二次项系数为5,
一次项系数为4,
常数项为0.
(3)2(t+2)=(t+1)2.
(3)t2-3=0,
二次项系数为1,
一次项系数为0,
常数项为-3.
知识点二 一元二次方程的解(根)
5.下列是方程5x2-4x-1=0的解的是( B )
A.x=-1 B.x=1 C.x=2 D.x=3
6.已知一元二次方程x2+kx-3=0有一个根为x=1,则k的值为( B )
A.-2 B.2 C.-4 D.4
【变式题】根据根的定义求字母的值→求代数式的值
(1)(2019·遂宁中考)已知关于x的一元二次方程(a-1)x2-2x+a2-1=0有一个根为x=0,则a的值为( D )
A.0 B.±1 C.1 D.-1
(2)(2019·兰州中考)已知x=1是关于x的一元二次方程x2+ax+2b=0的解,则2a+4b=( A )
A.-2 B.-3 C.-1 D.-6
(3)若2n(n≠0)是关于x的方程x2-2mx+2n=0的根,求m-n的值.
解:∵2n是方程x2-2mx+2n=0的根,
∴4n2-4mn+2n=0.
∵n≠0,
∴4n-4m+2=0.
∴4m-4n=2. ∴m-n= .
知识点三 用一元二次方程刻画实际问题中的数
量关系
7.为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为 .
x(x+40)=1200
8.某校要组织一次乒乓球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排2天,每天安排5场比赛.设比赛组织者应邀请x个队参赛,则x满足的方程为 .
9.(2019·潮南区一模)若关于x的一元二次方程(m-2)x2+5x+m2-4=0的常数项是0,则( D )
A.m=4 B.m=2
C.m=2或m=-2 D.m=-2
10.(2019·武汉期末)第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,小郑幸运获得了一张军运会吉祥物“兵兵”的照片.如图,该照片(中间的矩形)长29 cm、宽为20 cm,她想为此照片配一个四条边宽度相等的镜框(阴影部分),且镜框所占面积为照片面积的 .
为求镜框的宽度,她设镜框的宽度为x cm,依题意列方程,化成一般式为 .
4x2+98x-145=0
11.一元二次方程a(x2+1)+b(x+2)+c=0化为一般式后为6x2+10x-1=0,则以a、b为两条对角线长的菱形的面积为 .
30
12.(2019·右玉县期末)在一元二次方程x2-2ax+b=0中,若a2-b>0,则称a是该方程的中点值.
(1)方程x2-8x+3=0的中点值是 ;
4
(2)已知x2-mx+n=0的中点值是3,其中一个根是2,求mn的值.
解:∵ =3,∴m=6.
把x=2代入x2-mx+n=0,
得4-6×2+n=0,解得n=8.
∴mn=6×8=48.
13.已知方程(m-2) +(m-3)x+1=0.
(1)当m为何值时,它是一元二次方程?
解:若原方程为一元二次方程,
则 解得m=
∴所以当m为 或 时,原方程为一元二次方程.
(2)当m为何值时,它是一元一次方程?
解:若原方程为一元一次方程,
则 或 或m=0.
解得m=2,±1或0.
∴所以当m为2或±1或0时,原方程为一元一次方程.
14.已知m是方程x2-x-3=0的一个实数根,求代数式(m2-m)(m- +1)的值.
解:∵m是方程x2-x-3=0的一个实数根,
∴m2-m-3=0,即m2-m=3.
∴易知m≠0.
在m2-m-3=0两边同时除以m,得m-1- =0,
即m- =1.
∴(m2-m)(m- +1)=3×(1+1)=6.
15.【注重传统文化】《九章算术》中记载:今有户不知高、广,竿不知长短.横之不出四尺,纵之不出二尺,邪之适出.问户高、广、邪各几何?
译文是:今有门,不知其高、宽,有竿,不知其长短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.
问门高、宽、对角线的长分别是多少?若设门对角线的长为x尺,根据题意列出方程并化为一般形式.
解:如图,由题设可知对角线AB的长为x尺,则门的宽度AC长为(x-4)尺,
门的高度BC长为(x-2)尺.
根据勾股定理得(x-4)2+(x-2)2=x2,
整理得x2-12x+20=0.
同课章节目录
