人教版数学六年级上册5.4圆的面积 课件(28张ppt)
文档属性
| 名称 | 人教版数学六年级上册5.4圆的面积 课件(28张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
第4课时 圆的面积
1.理解圆的面积的意义,掌握圆的面积的计算公式,
能正确地计算圆的面积,会运用圆面积的计算公式
解决实际问题。(重点)
2.理解圆的面积公式的推导过程。(难点)
我们学习过哪些平面图形的面积?它们的计算公式各是什么?
长方形:长×宽 正方形:边长×边长
平行四边形:底×高 三角形:底×高÷2
梯形:(上底+下底)×高÷2
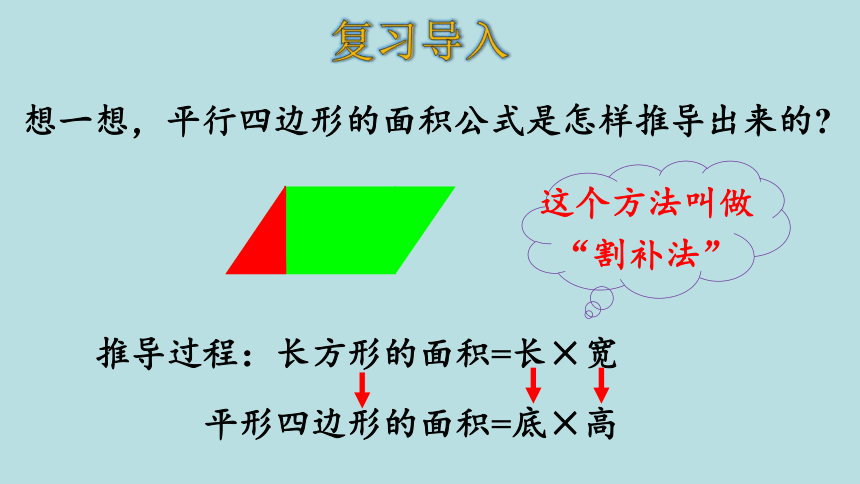
想一想,平行四边形的面积公式是怎样推导出来的
推导过程:长方形的面积=长×宽
平形四边形的面积=底×高
这个方法叫做
“割补法”
想一想长方形和正方形的面积。
圆的面积的意义
说一说你认为的圆的面积是什么?
圆所占平面的大小叫做圆的面积。
想一想,圆的面积公式应该如何推导出来呢?
圆的面积公式能不能通过 “割补法” 转化成我们已学过的图形来推导出来呢?
回想如何推导
平行四边形面
积公式的?
你想把圆转化成什么图形呢?与小组同学合作完成。
四
等
分
八
等
分
十六等分
三
十
二
等
分
以拼成的近似平行四边形为例:
圆面8等分时:
圆面16等分时:
圆面32等分时:
你有什么发现?
发现:把圆平均分成的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
从图中可以看出,长方形的长近似于圆的周长的一半(πr),宽近似于圆的半径(r)。
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
如果用S 表示圆的面积,那么圆的面积计算公式就是 :
长
宽
πr
r
πr
S=πr
知识提炼
1.圆所占平面的大小叫做圆的面积。
2.圆的面积近似等于拼成的长方形的面积,圆的面积公式是S=πr 。
圆形草坪的直径是20m,每平方米草皮8元,铺满草皮需要多少钱
20÷2=10(m)
314×8=2512(元)
3.14×10 =314(m )
答:铺满草皮需要2512元。
从题目中你都知道了什么?
要求铺满草坪需要多少钱,先要求出圆形草坪的面积是多少平方米。
知识提炼
计算圆的面积时,可根据条件选择相对应的公式。
(1)已知r 求S ,用公式 S =πr2;
(2)已知d 求S ,用公式 S =π( )2;
(3)已知C 求S ,用公式 S =π( )2。
d2
C
2π
小试牛刀
一个圆形茶几桌面的直径是1 m,它的面积是多少平方米?(选自教材P68做一做第1题)
3.14×0.52=0.785(平方米)
答:它的面积是0.785平方米。
1÷2=0.5(米)
正确答案:×
点拨: 两者数值虽然相同,但是表示的意义截然不同,无法进行
比较。
此题错在把长度单位和面积单位进行了比较。
37.68÷3.14÷2=6(米)
3.14×62=113.04(平方米)
1.
答:这个花坛的占地面积是113.04平方米。
答:这只羊最多可以吃到78.5平方米。
2.
3.14×52=78.5(平方米)
31.4×2÷3.14÷2=10(米)
3.
答:这个鸡圈占地面积是157平方米。
3.14×102÷2=157(平方米)
4. 完成下表。
半径 直径 圆面积
4 cm
9 cm
6 cm
20 cm
4.5 cm
3 cm
8 cm
40 cm
50.24 cm
63.585 cm
28.26 cm
1256 cm
(选自教材P71练习十五第1题)
5.计算下面各圆的周长和面积。(选自教材P71练习十五第2题)
大圆:3.14×10=31.4(cm)
3.14×(10÷2)2=78.5(cm2)
小圆:2×3.14×3=18.84(cm)
3.14×32=28.26(cm2)
6.公园草地上一个自动旋转喷灌装置的射程是10 m,它能喷灌的面积是多少?(选自教材P71练习十五第3题)
3.14×102=314(m2)
答:它能喷灌的面积是314m 。
1.圆所占平面的大小叫做圆的面积。
2.圆的面积近似等于拼成的长方形的面积,圆的面
积公式是S=πr 。
3.计算圆的面积时,可根据条件选择相对应的公式。
(1)已知 r 求 S ,用公式 S = πr2;
(2)已知 d 求 S ,用公式 S =π( )2;
(3)已知 C 求 S ,用公式 S =π( )2。
d2
C
2π
作业1:完成教材P71练习十五。
作业2:完成教材详解对应的练习题。
第4课时 圆的面积
1.理解圆的面积的意义,掌握圆的面积的计算公式,
能正确地计算圆的面积,会运用圆面积的计算公式
解决实际问题。(重点)
2.理解圆的面积公式的推导过程。(难点)
我们学习过哪些平面图形的面积?它们的计算公式各是什么?
长方形:长×宽 正方形:边长×边长
平行四边形:底×高 三角形:底×高÷2
梯形:(上底+下底)×高÷2
想一想,平行四边形的面积公式是怎样推导出来的
推导过程:长方形的面积=长×宽
平形四边形的面积=底×高
这个方法叫做
“割补法”
想一想长方形和正方形的面积。
圆的面积的意义
说一说你认为的圆的面积是什么?
圆所占平面的大小叫做圆的面积。
想一想,圆的面积公式应该如何推导出来呢?
圆的面积公式能不能通过 “割补法” 转化成我们已学过的图形来推导出来呢?
回想如何推导
平行四边形面
积公式的?
你想把圆转化成什么图形呢?与小组同学合作完成。
四
等
分
八
等
分
十六等分
三
十
二
等
分
以拼成的近似平行四边形为例:
圆面8等分时:
圆面16等分时:
圆面32等分时:
你有什么发现?
发现:把圆平均分成的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
从图中可以看出,长方形的长近似于圆的周长的一半(πr),宽近似于圆的半径(r)。
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
如果用S 表示圆的面积,那么圆的面积计算公式就是 :
长
宽
πr
r
πr
S=πr
知识提炼
1.圆所占平面的大小叫做圆的面积。
2.圆的面积近似等于拼成的长方形的面积,圆的面积公式是S=πr 。
圆形草坪的直径是20m,每平方米草皮8元,铺满草皮需要多少钱
20÷2=10(m)
314×8=2512(元)
3.14×10 =314(m )
答:铺满草皮需要2512元。
从题目中你都知道了什么?
要求铺满草坪需要多少钱,先要求出圆形草坪的面积是多少平方米。
知识提炼
计算圆的面积时,可根据条件选择相对应的公式。
(1)已知r 求S ,用公式 S =πr2;
(2)已知d 求S ,用公式 S =π( )2;
(3)已知C 求S ,用公式 S =π( )2。
d2
C
2π
小试牛刀
一个圆形茶几桌面的直径是1 m,它的面积是多少平方米?(选自教材P68做一做第1题)
3.14×0.52=0.785(平方米)
答:它的面积是0.785平方米。
1÷2=0.5(米)
正确答案:×
点拨: 两者数值虽然相同,但是表示的意义截然不同,无法进行
比较。
此题错在把长度单位和面积单位进行了比较。
37.68÷3.14÷2=6(米)
3.14×62=113.04(平方米)
1.
答:这个花坛的占地面积是113.04平方米。
答:这只羊最多可以吃到78.5平方米。
2.
3.14×52=78.5(平方米)
31.4×2÷3.14÷2=10(米)
3.
答:这个鸡圈占地面积是157平方米。
3.14×102÷2=157(平方米)
4. 完成下表。
半径 直径 圆面积
4 cm
9 cm
6 cm
20 cm
4.5 cm
3 cm
8 cm
40 cm
50.24 cm
63.585 cm
28.26 cm
1256 cm
(选自教材P71练习十五第1题)
5.计算下面各圆的周长和面积。(选自教材P71练习十五第2题)
大圆:3.14×10=31.4(cm)
3.14×(10÷2)2=78.5(cm2)
小圆:2×3.14×3=18.84(cm)
3.14×32=28.26(cm2)
6.公园草地上一个自动旋转喷灌装置的射程是10 m,它能喷灌的面积是多少?(选自教材P71练习十五第3题)
3.14×102=314(m2)
答:它能喷灌的面积是314m 。
1.圆所占平面的大小叫做圆的面积。
2.圆的面积近似等于拼成的长方形的面积,圆的面
积公式是S=πr 。
3.计算圆的面积时,可根据条件选择相对应的公式。
(1)已知 r 求 S ,用公式 S = πr2;
(2)已知 d 求 S ,用公式 S =π( )2;
(3)已知 C 求 S ,用公式 S =π( )2。
d2
C
2π
作业1:完成教材P71练习十五。
作业2:完成教材详解对应的练习题。
