人教版七年级数学上册第二章整式的加减复习课课件(20张ppt)
文档属性
| 名称 | 人教版七年级数学上册第二章整式的加减复习课课件(20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 256.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 22:00:59 | ||
图片预览






文档简介
(共20张PPT)
第二章
整式的加减
复习课
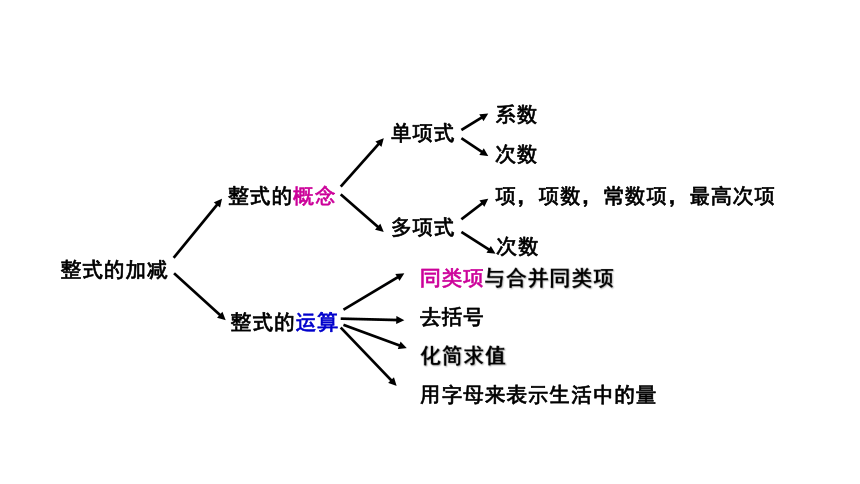
整式的加减
整式的概念
整式的运算
单项式
多项式
系数
次数
项,项数,常数项,最高次项
次数
同类项与合并同类项
去括号
化简求值
用字母来表示生活中的量
一、复习回顾
单项式:
定义:
系数:
次数:
由_________________组成的式子.
单独的
或
也是单项式.
数字或字母的乘积
一个数
一个字母
单项式中的_________.
单项式中的__________________.
数字因数
所有字母的指数和
注意的问题:
1.
当单项式的系数是
1
或
-1
时,“1”通常省略不写.
2.
当式子分母中出现字母时不是单项式.
3.
圆周率
π
是常数,不要看成字母.
4.
当单项式的系数是带分数时,通常写成假分数.
5.
单项式的系数应包括它前面的性质符号.
6.
单项式次数是指所有字母的次数的和,与数字的次数没有关系.
7.
单独的数字不含字母,规定它的次数是零次.
一、复习回顾
多项式
定义:几个__________.
项:组成多项式中的_____________.
有几项,就叫做_________.
常数项:多项式中_______________.
多项式的次数:____________________________.
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数
注意的问题:
1.
在确定多项式的项时,要连同它前面的符号.
2.
一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式.
3.
在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念.
一、复习回顾
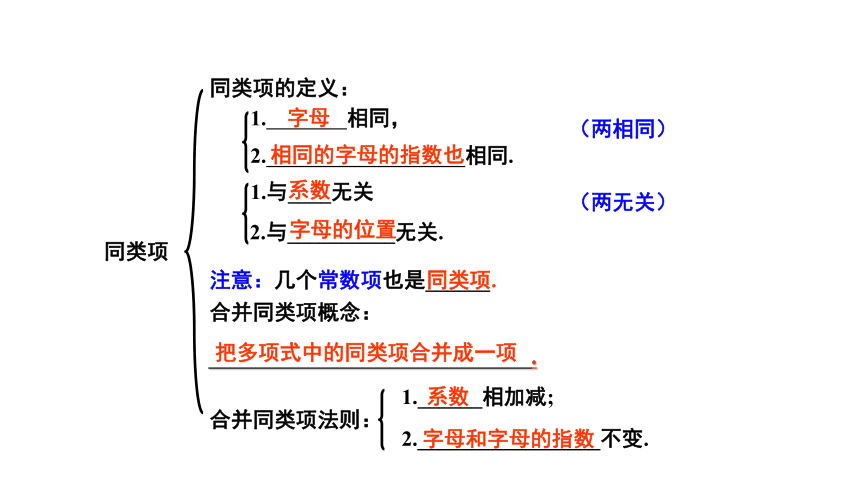
同类项
同类项的定义:
合并同类项概念:
合并同类项法则:
1.
相同,
2.
相同.
字母
相同的字母的指数也
(两相同)
1.与____无关
2.与__________无关.
系数
字母的位置
(两无关)
注意:几个常数项也是______
同类项.
.
把多项式中的同类项合并成一项
1.______相加减;
2._________________不变.
系数
字母和字母的指数
一、复习回顾
整式的加减混合运算步骤(有括号先去括号)
(一)去括号
(按照先小括号,再中括号,最后大括号的顺序)
1.
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
2.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
“去括号,看符号.是
‘+’号,不变号,是‘-’号,全变号”.
(二)计算
1.
找同类项,做好标记.
2.
利用加法的交换律和结合律把同类项放在一起.
3.
利用乘法分配律计算结果.
4.
按要求按“升”或“降”幂排列.
找
搬
并
排
一、复习回顾
1.
单项式的定义
例1
下列各式子中,是单项式的有______________(填序号).
注意:
1.
单个的字母或数字也是单项式;
2.
用加减号把数字或字母连接在一起的式子不是单项式;
3.
只用乘号把数字或字母连接在一起的式子仍是单项式;
4.
当式子中出现分母时,要留意分母里有没有字母,有字母的就不是单项式,如果分母没有字母的仍有可能是单项式.
(注:“π”
当作数字,而不是字母)
①②④⑦
二、典例精析
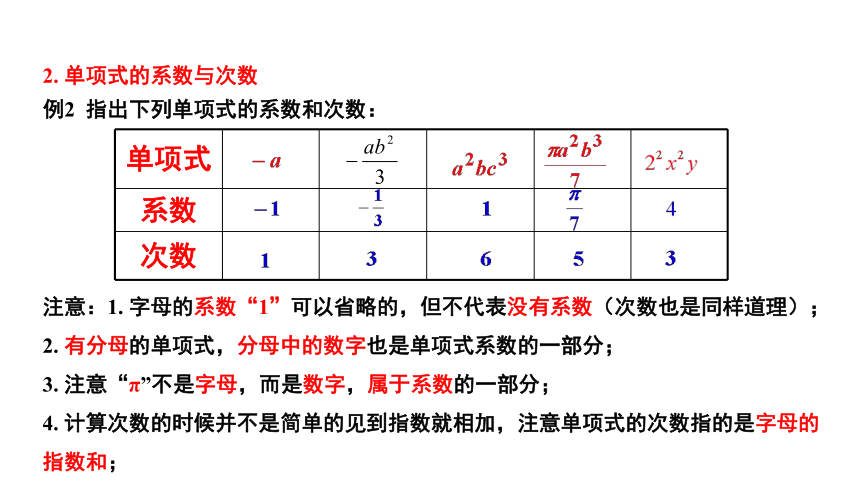
2.
单项式的系数与次数
例2
指出下列单项式的系数和次数:
单项式
系数
次数
注意:1.
字母的系数“1”可以省略的,但不代表没有系数(次数也是同样道理);
2.
有分母的单项式,分母中的数字也是单项式系数的一部分;
3.
注意“π”不是字母,而是数字,属于系数的一部分;
4.
计算次数的时候并不是简单的见到指数就相加,注意单项式的次数指的是字母的指数和;
二、典例精析
3.
多项式的项数与次数
例3
下列多项式次数为
3
的是(
)
C
注意:(1)多项式的次数不是所有项的次数的和,而是它的最高次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次,“π”当作数字,而不是字母.
例4
请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项.
四
三
二、典例精析
4.
书写格式中的易错点
例5
下列各个式子中,书写格式正确的是(
)
F
1.
代数式中用到乘法时,若是数字与数字乘,要用“×若是数字与字母乘,乘号通常写成“.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与字母相乘,乘号通常写成“·”
或省略不写.
2.
带分数与字母相乘,要写成假分数.
3.
代数式中出现除法运算时,一般用分数写,即用分数线代替除号.
4.
系数一般写在字母的前面,且系数“1”
往往会省略.
二、典例精析
例6
王强班上有男生
m
人,女生比男生的一半多
5
人,王强班上的总人数(用m表示)为______人.
易错点:结果不进行化简,直接写
点拨:结果中有
它们是同类项,应合并以保证最后的结果最简.
正确的写法是
二、典例精析
同类项的判定与合并同类项的法则:
1.
判断下列各式是否是同类项?
点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;
答:(2)、(4)是同类项,(1)(3)不是同类项.
三、随堂练习
2.下列合并同类项的结果错误的有
.
注意:1.
合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2.
合并同类项后也要注意书写格式;
3.
如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
①、②、③、④、⑤
三、随堂练习
3.合并同类项:
小明的解法:
(1)错在把所有项都当作同类项了;
正确的解法:
三、随堂练习
小明的解法:
正确的解法:
(2)错在把结合同类项时弄错了符号;
总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的.
三、随堂练习
3.合并同类项:
去括号中的易错题:
1.判断下列各式是否正确:
(
)
×
(
)
×
(
)
×
(
)
√
去括号时,注意:
1.
括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号.
2.外面有系数的,各项都要乘以那个系数.
三、随堂练习
化简求值中的易错题:
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时,
(代入)
(代入时注意添上括号,乘号改回“×”)
三、随堂练习
“A+2B”类型的易错题:
若多项式
计算多项式A
-
2B;
注意:列式时要先加上括号,再去括号.
三、随堂练习
通过对本章内容的复习,你有哪些新的收获?
对整式及其相关概念“是什么”、“之间有哪些联系”、
“有什么用”等方面的认识是否有所提高;
2.
是否更加清晰地认识到进行整式的加减实际上就是将整式化简,而化简的主要方法是合并多项式中的同类项和去括号.
四、小结
再
见
第二章
整式的加减
复习课
整式的加减
整式的概念
整式的运算
单项式
多项式
系数
次数
项,项数,常数项,最高次项
次数
同类项与合并同类项
去括号
化简求值
用字母来表示生活中的量
一、复习回顾
单项式:
定义:
系数:
次数:
由_________________组成的式子.
单独的
或
也是单项式.
数字或字母的乘积
一个数
一个字母
单项式中的_________.
单项式中的__________________.
数字因数
所有字母的指数和
注意的问题:
1.
当单项式的系数是
1
或
-1
时,“1”通常省略不写.
2.
当式子分母中出现字母时不是单项式.
3.
圆周率
π
是常数,不要看成字母.
4.
当单项式的系数是带分数时,通常写成假分数.
5.
单项式的系数应包括它前面的性质符号.
6.
单项式次数是指所有字母的次数的和,与数字的次数没有关系.
7.
单独的数字不含字母,规定它的次数是零次.
一、复习回顾
多项式
定义:几个__________.
项:组成多项式中的_____________.
有几项,就叫做_________.
常数项:多项式中_______________.
多项式的次数:____________________________.
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数
注意的问题:
1.
在确定多项式的项时,要连同它前面的符号.
2.
一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式.
3.
在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念.
一、复习回顾
同类项
同类项的定义:
合并同类项概念:
合并同类项法则:
1.
相同,
2.
相同.
字母
相同的字母的指数也
(两相同)
1.与____无关
2.与__________无关.
系数
字母的位置
(两无关)
注意:几个常数项也是______
同类项.
.
把多项式中的同类项合并成一项
1.______相加减;
2._________________不变.
系数
字母和字母的指数
一、复习回顾
整式的加减混合运算步骤(有括号先去括号)
(一)去括号
(按照先小括号,再中括号,最后大括号的顺序)
1.
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
2.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
“去括号,看符号.是
‘+’号,不变号,是‘-’号,全变号”.
(二)计算
1.
找同类项,做好标记.
2.
利用加法的交换律和结合律把同类项放在一起.
3.
利用乘法分配律计算结果.
4.
按要求按“升”或“降”幂排列.
找
搬
并
排
一、复习回顾
1.
单项式的定义
例1
下列各式子中,是单项式的有______________(填序号).
注意:
1.
单个的字母或数字也是单项式;
2.
用加减号把数字或字母连接在一起的式子不是单项式;
3.
只用乘号把数字或字母连接在一起的式子仍是单项式;
4.
当式子中出现分母时,要留意分母里有没有字母,有字母的就不是单项式,如果分母没有字母的仍有可能是单项式.
(注:“π”
当作数字,而不是字母)
①②④⑦
二、典例精析
2.
单项式的系数与次数
例2
指出下列单项式的系数和次数:
单项式
系数
次数
注意:1.
字母的系数“1”可以省略的,但不代表没有系数(次数也是同样道理);
2.
有分母的单项式,分母中的数字也是单项式系数的一部分;
3.
注意“π”不是字母,而是数字,属于系数的一部分;
4.
计算次数的时候并不是简单的见到指数就相加,注意单项式的次数指的是字母的指数和;
二、典例精析
3.
多项式的项数与次数
例3
下列多项式次数为
3
的是(
)
C
注意:(1)多项式的次数不是所有项的次数的和,而是它的最高次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次,“π”当作数字,而不是字母.
例4
请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项.
四
三
二、典例精析
4.
书写格式中的易错点
例5
下列各个式子中,书写格式正确的是(
)
F
1.
代数式中用到乘法时,若是数字与数字乘,要用“×若是数字与字母乘,乘号通常写成“.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与字母相乘,乘号通常写成“·”
或省略不写.
2.
带分数与字母相乘,要写成假分数.
3.
代数式中出现除法运算时,一般用分数写,即用分数线代替除号.
4.
系数一般写在字母的前面,且系数“1”
往往会省略.
二、典例精析
例6
王强班上有男生
m
人,女生比男生的一半多
5
人,王强班上的总人数(用m表示)为______人.
易错点:结果不进行化简,直接写
点拨:结果中有
它们是同类项,应合并以保证最后的结果最简.
正确的写法是
二、典例精析
同类项的判定与合并同类项的法则:
1.
判断下列各式是否是同类项?
点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;
答:(2)、(4)是同类项,(1)(3)不是同类项.
三、随堂练习
2.下列合并同类项的结果错误的有
.
注意:1.
合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2.
合并同类项后也要注意书写格式;
3.
如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
①、②、③、④、⑤
三、随堂练习
3.合并同类项:
小明的解法:
(1)错在把所有项都当作同类项了;
正确的解法:
三、随堂练习
小明的解法:
正确的解法:
(2)错在把结合同类项时弄错了符号;
总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的.
三、随堂练习
3.合并同类项:
去括号中的易错题:
1.判断下列各式是否正确:
(
)
×
(
)
×
(
)
×
(
)
√
去括号时,注意:
1.
括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号.
2.外面有系数的,各项都要乘以那个系数.
三、随堂练习
化简求值中的易错题:
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时,
(代入)
(代入时注意添上括号,乘号改回“×”)
三、随堂练习
“A+2B”类型的易错题:
若多项式
计算多项式A
-
2B;
注意:列式时要先加上括号,再去括号.
三、随堂练习
通过对本章内容的复习,你有哪些新的收获?
对整式及其相关概念“是什么”、“之间有哪些联系”、
“有什么用”等方面的认识是否有所提高;
2.
是否更加清晰地认识到进行整式的加减实际上就是将整式化简,而化简的主要方法是合并多项式中的同类项和去括号.
四、小结
再
见
