人教版高中物理选修3-3 8.3理想气体状态方程(共44张PPT)
文档属性
| 名称 | 人教版高中物理选修3-3 8.3理想气体状态方程(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-09 06:53:19 | ||
图片预览










文档简介
(共44张PPT)
理想气体的状态方程
教学目标
了解理想气体的模型,并知道实际气体在什么情况下可以看成理想气体
能够从气体定律推出理想气体的状态方程
掌握理想气体状态方程的内容和表达式,并能应用方程解决实际问题
通过由气体的实验定律推出理想气体的状态方程,培养学生的推力能力和抽象思维能力
教学重点
教学难点
理想气体的状态方程
理想气体状态方程的内容及表达式
知道理想气体状态方程的使用条件
利用理想气体状态方程求解有关问题
理想气体的理解
利用理想气体状态方程求解有关问题
前情回顾
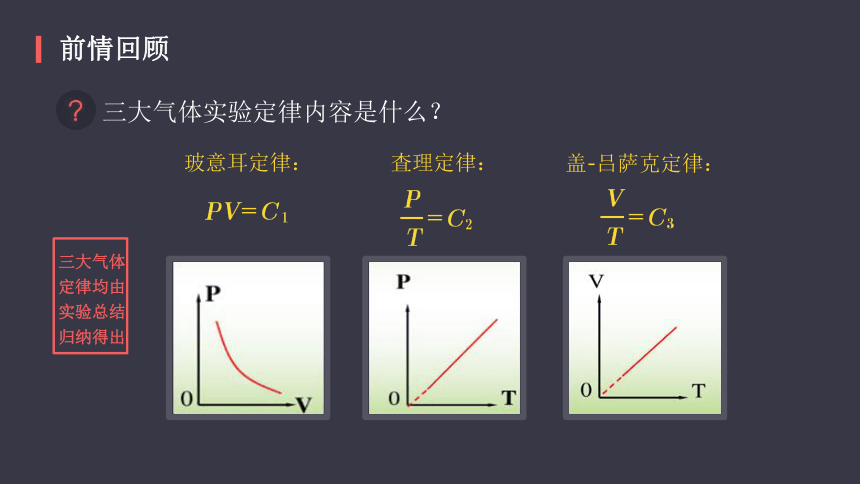
三大气体实验定律内容是什么?
玻意耳定律:
査理定律:
盖-吕萨克定律:
三大气体定律均由实验总结归纳得出
前情回顾
这些定律的适用范围是什么?
温度不太低(与常温比较),压强不太大(与大气压强相比)。
空气
1?
?
?
?
?
?
?
?
?1.000?
?
?
?
?
?
?
?1.000?
?
?
?
?
?
?
1.000?
?
?
?
?
?
?
?
?1.000
100?
?
?
?
?
?
?
?1.0690?
?
?
?
?
?
?0.9941?
?
?
?
?
?0.9265?
?
?
?
?
?
?
?0.9730
200?
?
?
?
?
?
?
?1.1380?
?
?
?
?
?
?1.0483?
?
?
?
?
?0.9140?
?
?
?
?
?
?
?1.0100
500?
?
?
?
?
?
?
?1.3565?
?
?
?
?
?
?1.3900?
?
?
?
?
?1.1560?
?
?
?
?
?
?
?1.3400
1000?
?
?
?
?
?
?
1.7200?
?
?
?
?
?
?2.0685?
?
?
?
?
?1.7355?
?
?
?
?
?
?
?1.9920
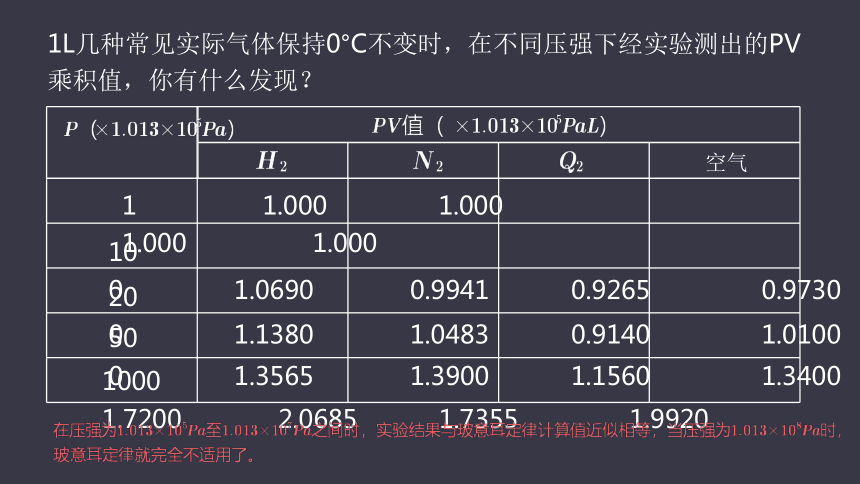
1L几种常见实际气体保持0°C不变时,在不同压强下经实验测出的PV乘积值,你有什么发现?
了解理想气体的模型
知道实际气体什么情况下可以看成理想气体
理想气体
理想气体
设想有这样一种气体,它在任何温度和任何压强下都能严格地遵从气体实验定律,我们把这样的气体叫做“理想气体”
理想气体的特点:
①严格遵守气体实验定律
②理想气体分子本身的大小与分子间的距离相比可以忽略不计,分子可视为质点;
③理想气体分子除碰撞外,无相互作用的引力和斥力。
理想气体
注意:
理想气体是为了研究问题方便而提出的一种理想模型,是实际气体的一种近似,实际上并不存在,就像力学中的质点、电学中的点电荷模型一样。
从宏观上讲,实际气体在压强不太大(不超过大气压的几倍)
、温度不太低(不低于零下几十摄氏度)的条件下,可视为理想气体。
如氢、氧气、氢气不易液化的气体。
理想气体
理想气体的理解
①理想气体是一种没有内部结构,不占有体积的刚性质点。
②气体分子在运动过程中,除碰撞的瞬间外,分子之间以及分子和器壁之间都无相互作用力。
③分子之间和分子与器壁之间的碰撞,都是完全弹性碰撞。除碰撞以外,分子的运动都是匀速直线运动,各个方向的运动机会均等。
理想气体
理想气体的理解
从微观上说:分子间以及分子和器壁间,除碰撞外无其他作用力,分子本身没有体积,即它所占据的空间认为都是可以被压缩的空间。
从能量上说:理想气体的微观本质是忽略了分子力,没有分子力做功,没有分子势能,于是理想气体的内能只有分子动能。
一定质量的理想气体的内能仅由温度决定,与气体的体积无关。
前面的三个实验定律都是对一定质量的气体在某一个量不变的情况下研究另外两个量的变化,那么这三个量都变化时三个量之间满足什么样的关系呢?
掌握理想气体状态方程的内容和表达式
会用理想气体状态方程解决实际问题
理想气体状态方程
探究三个量都变化时遵从的规律
如图所示,一定质量的某种理想气体
从A到B经历了一个等温过程,
从B到C经历了一个等容过程。
那么A、C状态的状态参量间有何关系呢?
探究三个量都变化时遵从的规律
从A→B为等温变化:由玻意耳定律
从B→C为等容变化:由查理定律
解得:
探究三个量都变化时遵从规律的反思
以上探究过程中先后经历了等温变化、等容变化两个过程,是否表示始末状态参量的关系与中间过程有关?
与中间过程无关,中间过程只是为了应用已学过的规律(如玻意耳定律、查理定律等)研究始末状态参量之间的关系而采用的一种手段。
探究三个量都变化时遵从规律的反思
从A→B为等容变化:由查理定律
从B→C为等压变化:由玻意耳定律
解得:
探究三个量都变化时遵从规律的反思
一般状态变化图象的处理方法:?
基本方法,化“一般”为“特殊”
如图是一定质量的某种气体的状态变化过程A-B-C-A。
在V-T图线上,等压线是一簇延长线过原点的直线,过A、B、C三点作三条等压线分别表示三个等压状态。
所以A→B压强增大,温度降低,体积缩小,
B
→
C温度升高,体积减小,压强增大,
C→A
温度降低,体积增大,压强减小。
理想气体状态方程
由于A、C两态是任意的,因此,上式可推广到任意的两态之间,即对一定质量的气体,无论其状态如何变化,都满足
理想气体状态方程
内容:一定质量的某种理想气体在从一个状态变化到另一个状态时,尽管p、V、T都可能改变,但是压强跟体积的乘积与热力学温度的比值保持不变
公式:
恒量C由理想气体的质量和种类决定,即由理想气体的物质的量决定
使用条件:一定质量的某种理想气体
不同种类的理想气体,具有相同的状态,同时具有相同的物质的量,这个恒量就相同。
或?
理想气体状态方程
理想气体状态方程与气体实验定律的关系
时,
时,
时,
(玻意耳定律)
(查理定律)
(盖·吕萨克定律)
由此可见,三个气体实验定律是理想气体状态方程的特例。
理想气体状态方程
P-V
P-T
P-t
名称?
?
?
?
?
?
?
?
?
?
?
?图象?
?
?
?
?
?
?
?
?
?
?
?特点?
?
?
?
?
?
?
?
?
?其他图象
等温线
等容线
pV=CT(C为常量),即pV之积越大的等温线对应的温度越高,离原点越远
斜率k=CT,即斜率越大,对应的温度越高
斜率k=C/V,即斜率越大,对应的体积越小
图线的延长线均过点(-273.12,0),斜率越大,对应的体积越小
一定质量的理想气体的各种图象
理想气体状态方程
名称?
?
?
?
?
?
?
?
?
?
?
?图象?
?
?
?
?
?
?
?
?
?
?
?特点?
?
?
?
?
?
?
?
?
?其他图象
等压线
V-T
V-t
斜率k=C/P,即斜率越大,对应的压强越小
V与t成线性关系,但不成正比,图线延长线均过(-273.12,0)点,斜率越大,对应的压强越小
理想气体状态方程的推论
请根据一定质量理想气体的状态方程推导出含有密度的表达式
理想气体状态方程的气体密度式
理想气体状态方程的应用
理想气体状态方程的应用
理想气体状态方程的应用
一水银气压计中混进了空气,因而在27℃,外界大气压为758mmHg时,这个水银气压计的读数为738mmHg,此时管中水银面距管顶80mm,当温度降至-3℃时,这个气压计的读数为743mmHg,求此时的实际大气压值为多少毫米汞柱?
解
以混进水银气压计的空气为研究对象
初状态:
末状态:
由理想气体状态方程得:
即:
解得
理想气体状态方程的应用
理想气体状态方程的应用要点
①选对象:根据题意,选出所研究的某一部分气体,这部分气体在状态变化过程中,其质量必须保持一定。
②找参量:找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值或表达式,压强的确定往往是个关键,常需结合力学知识(女力的平衡条件或牛顿运动定律)才能写出表达式。
理想气体状态方程的应用
理想气体状态方程的应用要点
③认过程:过程表示两个状态之间的一种变化式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定认清变化过程是正确选用物理规律的前提。
④列方程:根据研究对象状态变化的具体方式、选用理想气体状态方程或某一实验定律,代入具体数值。T必须用热力学温度,p、v的单位要统一,最后分析讨论所得结果的合理性及其物理意义。
克拉珀龙方程
常量的大小与什么有关?
令
则
克拉珀龙方程
或
?
门捷列夫
克拉伯龙
克拉珀龙方程
克拉伯龙方程
或
摩尔气体常量
P(atm),V
(L):
R=0.082
atm·L/mol·K
容器内装有质量为0.10kg的氧气,压强为p=10×?
?
?
pa,温度为47°C。因为容器漏气,经过若干时间后,压强降为原来的八分之五,温度降到27°C。问容器的容积有多大?漏去了多少氧气?(假设氧气看作理想气体)
克拉珀龙方程
解(1)根据理想气体的状态方程,
求得容器的体积V为
容器内装有质量为0.10kg的氧气,压强为P
=10×?
?
?
pa,温度为47°C。因为容器漏气,经过若干时间后,压强降为原来的八分之五,温度降到27°C。问容器的容积有多大?漏去了多少氧气?(假设氧气看作理想气体)
解(2)设漏气若干时间后,压强减少到P’,温度降到T’。如果用M’表示容器中剩余的氧气质量,由理想气体状态方程得
所以漏去氧气的质量为
混合理想气体的状态方程
前面的讨论只限于化学成分单一的理想气体,而在许多实际问题中,往往遇到包含多种不同组分的气体。如果混合气体的各组分可视为理想气体,而各组分之间又无化学反应,我们就可求得混合理想气体的状态方程。
道尔顿分压定律:
稀薄混合气体的总压强,等于各组分的分压强之和,即
说明:
①各组分的压强:这个组分在与混合气体同体积、同温度的条件下单独存在时的压强。
②定律只适用于理想气体。
混合理想气体的状态方程
方程的推导:
设混合气体由n种组分组成
当各组分与混合气体同体积同温度而单独存在时,对它们分别应用理想气体状态方程:
得:
……
……
各式想加,得:
即:
混合理想气体的状态方程
方程的推导:
其中P为混合气体的压强。
混合气体的状态方程
PV=vRT
可见,混合气体的状态方程与单一成分的相似,只是摩尔数等于各组分的摩尔数之和。
所以,从形式上看,混合气体好像也具有一定的摩尔质量,称为平均摩尔质量:
混合理想气体的状态方程
方程的推导:
所以,混合气体的状态方程可写为:
混合理想气体的状态方程
按质量百分比来说,空气中含有氮气76.9%,氧气23.1%.
求:
(1)空气的摩尔质量;
(2)空气在标准状态下的密度。
解:设空气质量为100g,则其中氮气76.9g,氧气23.1g。
混合理想气体的状态方程
按质量百分比来说,空气中含有氮气76.9%,氧气23.1%.
求:
(1)空气的摩尔质量;
(2)空气在标准状态下的密度。
解:
问题与练习
对一定质量的气体来说,能否做到以下各点?
(1)保持压强和体积不变而改变它的温度。
(2)保持压强不变,同时升高温度并减小体积。
(3)保持温度不变,同时增加体积并减小压强。
(4)保持体积不变,同时增加压强并降低温度。
不可能
不可能
不可能
不可能
问题与练习
根据理想气体状态方程:
有
换算成摄氏温度
即汽缸中的压缩空气的温度约为668°C
问题与练习
在做托里拆利实验时,玻璃管内有些残存的空气,此时玻璃管竖直放置,如图所示。假如把玻璃管竖直向上提起一段距离,玻璃管下端仍浸在水银中,则管内空气体积如何变化?管内水银柱长度如何变化?管内空气压强如何变化?
由于外界大气压不变,玻璃管内空气含量较少,对压强影响不是很大。因此,当玻璃管竖直向上提起时,管内水银柱的高度变化不会很大,管内空气柱长度增加,体积增大。我们可以把这个过程看做等温过程,由于体积增大,玻璃管内空气压强会减小,水银柱的长度会增加
总结
理想气体(理想化模型):
在任何温度和任何压强下都能严格地遵从气体实验定律的气体
理想气体的状态方程
或
注:恒量C由理想气体的质量和种类决定,即由气体的物质的量决定
气体密度式:
理想气体的状态方程
教学目标
了解理想气体的模型,并知道实际气体在什么情况下可以看成理想气体
能够从气体定律推出理想气体的状态方程
掌握理想气体状态方程的内容和表达式,并能应用方程解决实际问题
通过由气体的实验定律推出理想气体的状态方程,培养学生的推力能力和抽象思维能力
教学重点
教学难点
理想气体的状态方程
理想气体状态方程的内容及表达式
知道理想气体状态方程的使用条件
利用理想气体状态方程求解有关问题
理想气体的理解
利用理想气体状态方程求解有关问题
前情回顾
三大气体实验定律内容是什么?
玻意耳定律:
査理定律:
盖-吕萨克定律:
三大气体定律均由实验总结归纳得出
前情回顾
这些定律的适用范围是什么?
温度不太低(与常温比较),压强不太大(与大气压强相比)。
空气
1?
?
?
?
?
?
?
?
?1.000?
?
?
?
?
?
?
?1.000?
?
?
?
?
?
?
1.000?
?
?
?
?
?
?
?
?1.000
100?
?
?
?
?
?
?
?1.0690?
?
?
?
?
?
?0.9941?
?
?
?
?
?0.9265?
?
?
?
?
?
?
?0.9730
200?
?
?
?
?
?
?
?1.1380?
?
?
?
?
?
?1.0483?
?
?
?
?
?0.9140?
?
?
?
?
?
?
?1.0100
500?
?
?
?
?
?
?
?1.3565?
?
?
?
?
?
?1.3900?
?
?
?
?
?1.1560?
?
?
?
?
?
?
?1.3400
1000?
?
?
?
?
?
?
1.7200?
?
?
?
?
?
?2.0685?
?
?
?
?
?1.7355?
?
?
?
?
?
?
?1.9920
1L几种常见实际气体保持0°C不变时,在不同压强下经实验测出的PV乘积值,你有什么发现?
了解理想气体的模型
知道实际气体什么情况下可以看成理想气体
理想气体
理想气体
设想有这样一种气体,它在任何温度和任何压强下都能严格地遵从气体实验定律,我们把这样的气体叫做“理想气体”
理想气体的特点:
①严格遵守气体实验定律
②理想气体分子本身的大小与分子间的距离相比可以忽略不计,分子可视为质点;
③理想气体分子除碰撞外,无相互作用的引力和斥力。
理想气体
注意:
理想气体是为了研究问题方便而提出的一种理想模型,是实际气体的一种近似,实际上并不存在,就像力学中的质点、电学中的点电荷模型一样。
从宏观上讲,实际气体在压强不太大(不超过大气压的几倍)
、温度不太低(不低于零下几十摄氏度)的条件下,可视为理想气体。
如氢、氧气、氢气不易液化的气体。
理想气体
理想气体的理解
①理想气体是一种没有内部结构,不占有体积的刚性质点。
②气体分子在运动过程中,除碰撞的瞬间外,分子之间以及分子和器壁之间都无相互作用力。
③分子之间和分子与器壁之间的碰撞,都是完全弹性碰撞。除碰撞以外,分子的运动都是匀速直线运动,各个方向的运动机会均等。
理想气体
理想气体的理解
从微观上说:分子间以及分子和器壁间,除碰撞外无其他作用力,分子本身没有体积,即它所占据的空间认为都是可以被压缩的空间。
从能量上说:理想气体的微观本质是忽略了分子力,没有分子力做功,没有分子势能,于是理想气体的内能只有分子动能。
一定质量的理想气体的内能仅由温度决定,与气体的体积无关。
前面的三个实验定律都是对一定质量的气体在某一个量不变的情况下研究另外两个量的变化,那么这三个量都变化时三个量之间满足什么样的关系呢?
掌握理想气体状态方程的内容和表达式
会用理想气体状态方程解决实际问题
理想气体状态方程
探究三个量都变化时遵从的规律
如图所示,一定质量的某种理想气体
从A到B经历了一个等温过程,
从B到C经历了一个等容过程。
那么A、C状态的状态参量间有何关系呢?
探究三个量都变化时遵从的规律
从A→B为等温变化:由玻意耳定律
从B→C为等容变化:由查理定律
解得:
探究三个量都变化时遵从规律的反思
以上探究过程中先后经历了等温变化、等容变化两个过程,是否表示始末状态参量的关系与中间过程有关?
与中间过程无关,中间过程只是为了应用已学过的规律(如玻意耳定律、查理定律等)研究始末状态参量之间的关系而采用的一种手段。
探究三个量都变化时遵从规律的反思
从A→B为等容变化:由查理定律
从B→C为等压变化:由玻意耳定律
解得:
探究三个量都变化时遵从规律的反思
一般状态变化图象的处理方法:?
基本方法,化“一般”为“特殊”
如图是一定质量的某种气体的状态变化过程A-B-C-A。
在V-T图线上,等压线是一簇延长线过原点的直线,过A、B、C三点作三条等压线分别表示三个等压状态。
所以A→B压强增大,温度降低,体积缩小,
B
→
C温度升高,体积减小,压强增大,
C→A
温度降低,体积增大,压强减小。
理想气体状态方程
由于A、C两态是任意的,因此,上式可推广到任意的两态之间,即对一定质量的气体,无论其状态如何变化,都满足
理想气体状态方程
内容:一定质量的某种理想气体在从一个状态变化到另一个状态时,尽管p、V、T都可能改变,但是压强跟体积的乘积与热力学温度的比值保持不变
公式:
恒量C由理想气体的质量和种类决定,即由理想气体的物质的量决定
使用条件:一定质量的某种理想气体
不同种类的理想气体,具有相同的状态,同时具有相同的物质的量,这个恒量就相同。
或?
理想气体状态方程
理想气体状态方程与气体实验定律的关系
时,
时,
时,
(玻意耳定律)
(查理定律)
(盖·吕萨克定律)
由此可见,三个气体实验定律是理想气体状态方程的特例。
理想气体状态方程
P-V
P-T
P-t
名称?
?
?
?
?
?
?
?
?
?
?
?图象?
?
?
?
?
?
?
?
?
?
?
?特点?
?
?
?
?
?
?
?
?
?其他图象
等温线
等容线
pV=CT(C为常量),即pV之积越大的等温线对应的温度越高,离原点越远
斜率k=CT,即斜率越大,对应的温度越高
斜率k=C/V,即斜率越大,对应的体积越小
图线的延长线均过点(-273.12,0),斜率越大,对应的体积越小
一定质量的理想气体的各种图象
理想气体状态方程
名称?
?
?
?
?
?
?
?
?
?
?
?图象?
?
?
?
?
?
?
?
?
?
?
?特点?
?
?
?
?
?
?
?
?
?其他图象
等压线
V-T
V-t
斜率k=C/P,即斜率越大,对应的压强越小
V与t成线性关系,但不成正比,图线延长线均过(-273.12,0)点,斜率越大,对应的压强越小
理想气体状态方程的推论
请根据一定质量理想气体的状态方程推导出含有密度的表达式
理想气体状态方程的气体密度式
理想气体状态方程的应用
理想气体状态方程的应用
理想气体状态方程的应用
一水银气压计中混进了空气,因而在27℃,外界大气压为758mmHg时,这个水银气压计的读数为738mmHg,此时管中水银面距管顶80mm,当温度降至-3℃时,这个气压计的读数为743mmHg,求此时的实际大气压值为多少毫米汞柱?
解
以混进水银气压计的空气为研究对象
初状态:
末状态:
由理想气体状态方程得:
即:
解得
理想气体状态方程的应用
理想气体状态方程的应用要点
①选对象:根据题意,选出所研究的某一部分气体,这部分气体在状态变化过程中,其质量必须保持一定。
②找参量:找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值或表达式,压强的确定往往是个关键,常需结合力学知识(女力的平衡条件或牛顿运动定律)才能写出表达式。
理想气体状态方程的应用
理想气体状态方程的应用要点
③认过程:过程表示两个状态之间的一种变化式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定认清变化过程是正确选用物理规律的前提。
④列方程:根据研究对象状态变化的具体方式、选用理想气体状态方程或某一实验定律,代入具体数值。T必须用热力学温度,p、v的单位要统一,最后分析讨论所得结果的合理性及其物理意义。
克拉珀龙方程
常量的大小与什么有关?
令
则
克拉珀龙方程
或
?
门捷列夫
克拉伯龙
克拉珀龙方程
克拉伯龙方程
或
摩尔气体常量
P(atm),V
(L):
R=0.082
atm·L/mol·K
容器内装有质量为0.10kg的氧气,压强为p=10×?
?
?
pa,温度为47°C。因为容器漏气,经过若干时间后,压强降为原来的八分之五,温度降到27°C。问容器的容积有多大?漏去了多少氧气?(假设氧气看作理想气体)
克拉珀龙方程
解(1)根据理想气体的状态方程,
求得容器的体积V为
容器内装有质量为0.10kg的氧气,压强为P
=10×?
?
?
pa,温度为47°C。因为容器漏气,经过若干时间后,压强降为原来的八分之五,温度降到27°C。问容器的容积有多大?漏去了多少氧气?(假设氧气看作理想气体)
解(2)设漏气若干时间后,压强减少到P’,温度降到T’。如果用M’表示容器中剩余的氧气质量,由理想气体状态方程得
所以漏去氧气的质量为
混合理想气体的状态方程
前面的讨论只限于化学成分单一的理想气体,而在许多实际问题中,往往遇到包含多种不同组分的气体。如果混合气体的各组分可视为理想气体,而各组分之间又无化学反应,我们就可求得混合理想气体的状态方程。
道尔顿分压定律:
稀薄混合气体的总压强,等于各组分的分压强之和,即
说明:
①各组分的压强:这个组分在与混合气体同体积、同温度的条件下单独存在时的压强。
②定律只适用于理想气体。
混合理想气体的状态方程
方程的推导:
设混合气体由n种组分组成
当各组分与混合气体同体积同温度而单独存在时,对它们分别应用理想气体状态方程:
得:
……
……
各式想加,得:
即:
混合理想气体的状态方程
方程的推导:
其中P为混合气体的压强。
混合气体的状态方程
PV=vRT
可见,混合气体的状态方程与单一成分的相似,只是摩尔数等于各组分的摩尔数之和。
所以,从形式上看,混合气体好像也具有一定的摩尔质量,称为平均摩尔质量:
混合理想气体的状态方程
方程的推导:
所以,混合气体的状态方程可写为:
混合理想气体的状态方程
按质量百分比来说,空气中含有氮气76.9%,氧气23.1%.
求:
(1)空气的摩尔质量;
(2)空气在标准状态下的密度。
解:设空气质量为100g,则其中氮气76.9g,氧气23.1g。
混合理想气体的状态方程
按质量百分比来说,空气中含有氮气76.9%,氧气23.1%.
求:
(1)空气的摩尔质量;
(2)空气在标准状态下的密度。
解:
问题与练习
对一定质量的气体来说,能否做到以下各点?
(1)保持压强和体积不变而改变它的温度。
(2)保持压强不变,同时升高温度并减小体积。
(3)保持温度不变,同时增加体积并减小压强。
(4)保持体积不变,同时增加压强并降低温度。
不可能
不可能
不可能
不可能
问题与练习
根据理想气体状态方程:
有
换算成摄氏温度
即汽缸中的压缩空气的温度约为668°C
问题与练习
在做托里拆利实验时,玻璃管内有些残存的空气,此时玻璃管竖直放置,如图所示。假如把玻璃管竖直向上提起一段距离,玻璃管下端仍浸在水银中,则管内空气体积如何变化?管内水银柱长度如何变化?管内空气压强如何变化?
由于外界大气压不变,玻璃管内空气含量较少,对压强影响不是很大。因此,当玻璃管竖直向上提起时,管内水银柱的高度变化不会很大,管内空气柱长度增加,体积增大。我们可以把这个过程看做等温过程,由于体积增大,玻璃管内空气压强会减小,水银柱的长度会增加
总结
理想气体(理想化模型):
在任何温度和任何压强下都能严格地遵从气体实验定律的气体
理想气体的状态方程
或
注:恒量C由理想气体的质量和种类决定,即由气体的物质的量决定
气体密度式:
