人教B版(2019)高中数学选择性必修第二册 4.2.1 随机变量及其与事件的联系 4.2.2 离散型随机变量的分布列(共36张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第二册 4.2.1 随机变量及其与事件的联系 4.2.2 离散型随机变量的分布列(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 847.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览









文档简介
4.2.1 随机变量及其与事件的联系
4.2.2 离散型随机变量的分布列
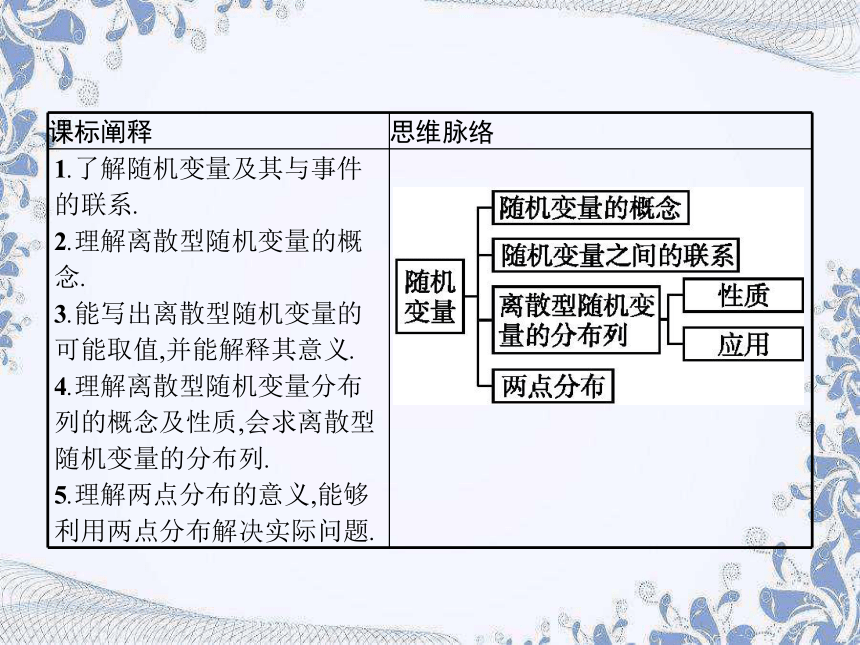
课标阐释
思维脉络
1.了解随机变量及其与事件的联系.
2.理解离散型随机变量的概念.
3.能写出离散型随机变量的可能取值,并能解释其意义.
4.理解离散型随机变量分布列的概念及性质,会求离散型随机变量的分布列.
5.理解两点分布的意义,能够利用两点分布解决实际问题.
激趣诱思
知识点拨
在射击比赛中,运动员射击一次,可能出现命中0环,命中1环,…,命中10环等结果,若用变量X来表示他一次射击所命中的环数,则变量X取值情况如何?(变量X的结果可能由0,1,…,10这11个数表示.)
激趣诱思
知识点拨
一、随机变量及其与事件的联系
1.随机变量
定义
一般地,如果随机试验的样本空间为Ω,而且对于Ω中的每一个样本点,变量X都对应有唯一确定的实数值,就称X为一个随机变量
表示
随机变量一般用大写英文字母X,Y,Z,…或小写希腊字母ξ,η,ζ,…表示
范围
随机变量所有可能的取值组成的集合,称为这个随机变量的取值范围
激趣诱思
知识点拨
2.随机变量与事件的联系
一般地,如果X是一个随机变量,a,b都是任意实数,那么X=a,X≤b,X>b等都表示事件,而且:
(1)当a≠b时,事件X=a与X=b互斥;
(2)事件X≤a与X>a相互对立,因此P(X≤a)+P(X>a)=1.
3.离散型随机变量
取值
特点
一一列出
对于随机变量所有可能取的值都能一一列举出来
有限性
离散型随机变量只取有限个值
激趣诱思
知识点拨
4.随机变量之间的关系
一般地,如果X是一个随机变量,a,b都是实数且a≠0,则Y=aX+b也是一个随机变量.
由于X=t的充要条件是Y=at+b,因此P(X=t)=P(Y=at+b).
名师点析 判断一个随机变量X是否为离散型随机变量的方法
(1)明确试验的所有可能结果;
(2)将随机试验的试验结果数量化;
(3)确定试验结果所对应的实数是否可按一定次序一一列出,如果能一一列举出来,那么该随机变量是离散型随机变量,否则不是.
激趣诱思
知识点拨
微思考1
若说随机变量就是函数,对吗?
提示:随机变量不一定为函数,函数是非空数集A,B间的一种对应,而随机变量间的对应是基本事件与实数间的对应.
微思考2
类似地,函数的定义域和值域相当于随机变量概念中的哪些量?
提示:随机变量与函数都是一种对应,试验结果的范围相当于函数的定义域,随机变量的取值范围相当于函数的值域.
微练习
若学校餐厅中午一共提供了1 000个馒头,则餐厅能卖出的馒头数X是否为随机变量?如果是,请写出它的取值.
解:是.X的所有可能取值为0,1,2,3,4,…,1 000.
激趣诱思
知识点拨
二、离散型随机变量的分布列
1.离散型随机变量的分布列
一般地,当离散型随机变量X的取值范围是{x1,x2,…,xn}时,如果对任意k∈{1,2,…,n},概率P(X=xk)=pk都是已知的,则称X的概率分布是已知的.离散型随机变量X的概率分布可以用如下形式的表格表示,这个表格称为X的概率分布或分布列.
X
x1
x2
…
xk
…
xn
P
p1
p2
…
pk
…
pn
离散型随机变量的分布列满足:
(1)pk≥0,k=1,2,…,n;
激趣诱思
知识点拨
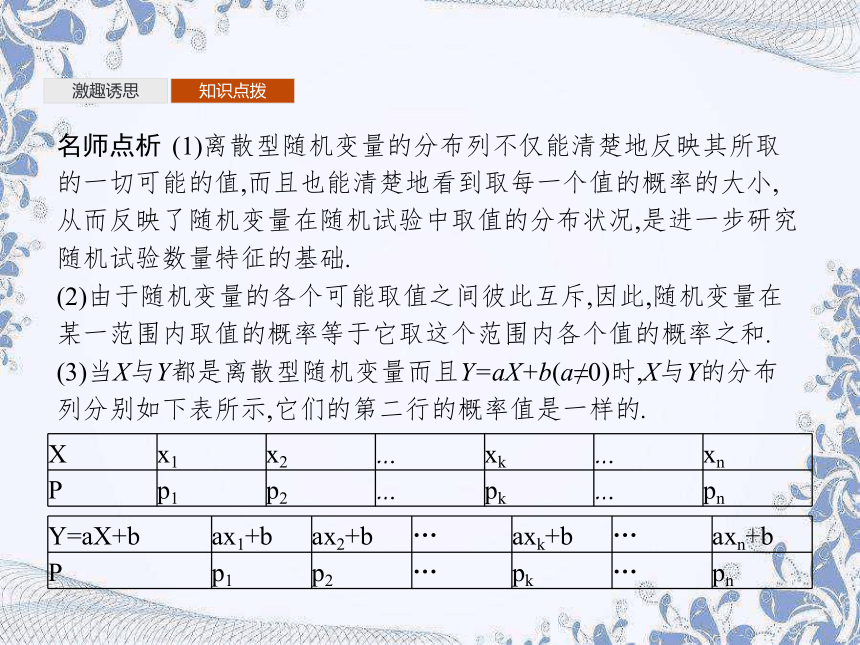
名师点析 (1)离散型随机变量的分布列不仅能清楚地反映其所取的一切可能的值,而且也能清楚地看到取每一个值的概率的大小,从而反映了随机变量在随机试验中取值的分布状况,是进一步研究随机试验数量特征的基础.
(2)由于随机变量的各个可能取值之间彼此互斥,因此,随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.
(3)当X与Y都是离散型随机变量而且Y=aX+b(a≠0)时,X与Y的分布列分别如下表所示,它们的第二行的概率值是一样的.
X
x1
x2
…
xk
…
xn
P
p1
p2
…
pk
…
pn
Y=aX+b
ax1+b
ax2+b
…
axk+b
…
axn+b
P
p1
p2
…
pk
…
pn
激趣诱思
知识点拨
2.两点分布
一般地,如果随机变量X的分布列为
其中0 名师点析 (1)两点分布又称为0-1分布或伯努利分布.
(2)两点分布的试验结果只有两个可能,且概率之和为1.
X
1
0
P
p
1-p
激趣诱思
知识点拨
微思考
如何根据定义求一个随机变量的分布列?
提示:其步骤为:①设出随机变量X,并确定X的所有可能取值,以及取每个值的意义;②计算X取每个值的概率;③写出X的分布列(一般列表).
激趣诱思
知识点拨
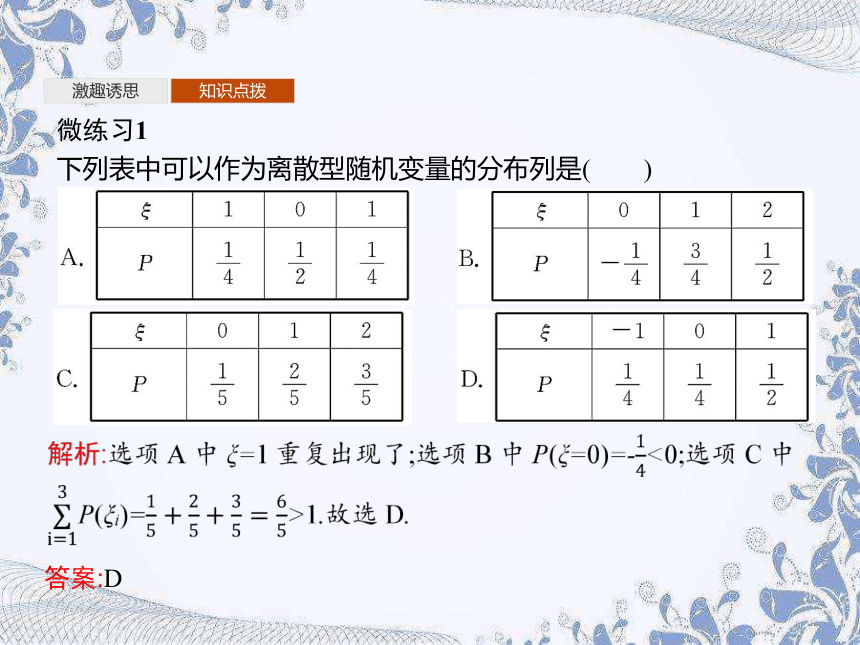
微练习1
下列表中可以作为离散型随机变量的分布列是( )
答案:D
激趣诱思
知识点拨
微练习2
X
0
1
P
?
?
探究一
探究二
探究三
探究四
素养形成
当堂检测
随机变量的可能取值及试验结果
例1写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果.
(1)一个袋中装有8个红球,3个白球,从中任取5个球,其中所含白球的个数为X.
(2)一个袋中有5个同样大小的黑球,编号为1,2,3,4,5,从中任取3个球,取出的球的最大号码记为X.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:(1)X=0表示取5个球全是红球;
X=1表示取1个白球,4个红球;
X=2表示取2个白球,3个红球;
X=3表示取3个白球,2个红球.
(2)X=3表示取出的球编号为1,2,3.
X=4表示取出的球编号为1,2,4;1,3,4或2,3,4.
X=5表示取出的球编号为1,2,5;1,3,5;1,4,5;2,3,5;2,4,5或3,4,5.
反思感悟 用随机变量表示随机试验的结果的关键点和注意点
(1)关键点:解决此类问题的关键是明确随机变量的所有可能取值,以及取每一个值对应的意义,即一个随机变量的取值对应一个或多个随机试验的结果.
(2)注意点:解答过程中不要漏掉某些试验结果.
探究一
探究二
探究三
探究四
素养形成
当堂检测
延伸探究 在本例(1)条件下,规定取出一个红球得2分,而每取出一个白球减1分,以ξ表示得的分数,结果如何?
解:ξ=10表示取5个球全是红球;
ξ=7表示取1个白球,4个红球;
ξ=4表示取2个白球,3个红球;
ξ=1表示取3个白球,2个红球.
探究一
探究二
探究三
探究四
素养形成
当堂检测
求离散型随机变量的分布列
例2一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的3只球中的最大号码,写出随机变量ξ的分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 求离散型随机变量分布列时应注意的问题
(1)确定离散型随机变量ξ的分布列的关键是要清楚ξ取每一个值对应的随机事件,进一步利用排列、组合知识求出ξ取每一个值的概率.
(2)在求离散型随机变量ξ的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可以验证分布列是否正确.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1某班有学生45人,其中是O型血的有10人,A型血的有12人,B型血的有8人,AB型血的有15人.现从中抽1人,其血型为随机变量X,求X的分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
离散型随机变量分布列的性质
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 利用离散型分布列的性质解题时要注意以下两个问题
(1)X=Xi(i=1,2,…,n)的各个取值表示的事件是互斥的.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练2若离散型随机变量X的分布列为
求常数a及相应的分布列.
X
0
1
P
4a-1
3a2+a
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
两点分布
例4已知一批200件的待出厂产品中,有1件不合格品,现从中任意抽取2件进行检查,若用随机变量X表示抽取的2件产品中的次品数,求X的分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 两点分布的4个特点
(1)两点分布中只有两个对应结果,且两结果是对立的;
(2)两点分布中的两个结果一个对应1,另一个对应0;
(3)由互斥事件的概率求法可知,已知P(X=0)(或P(X=1)),便可求出P(X=1)(或P(X=0)).
(4)在有多个结果的随机试验中,如果我们只关心一个随机事件是否发生,就可以利用两点分布来研究它.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练3设某项试验的成功率是失败率的2倍,用随机变量X描述一次试验的成功次数,则P(X=0)等于( )
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
求离散型随机变量y=f(ξ)的分布列
典例 设离散型随机变量X的分布列为
求:(1)2X+1的分布列;
(2)|X-1|的分布列.
X
0
1
2
3
4
P
0.2
0.1
0.1
0.3
m
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:由分布列的性质知0.2+0.1+0.1+0.3+m=1,
解得m=0.3.
首先列表为
从而由上表得两个分布列为
(1)2X+1的分布列
(2)|X-1|的分布列
X
0
1
2
3
4
2X+1
1
3
5
7
9
|X-1|
1
0
1
2
3
2X+1
1
3
5
7
9
P
0.2
0.1
0.1
0.3
0.3
|X-1|
0
1
2
3
P
0.1
0.3
0.3
0.3
探究一
探究二
探究三
探究四
素养形成
当堂检测
方法点睛 (1)若ξ是一个随机变量,a,b是常数,且a≠0,则η=aξ+b也是一个随机变量,推广到一般情况有:若ξ是随机变量,f(ξ)是连续函数或单调函数,则η=f(ξ)也是随机变量,也就是说,随机变量的某些函数值也是随机变量,并且若ξ为离散型随机变量,则η=f(ξ)也为离散型随机变量.
(2)已知离散型随机变量ξ的分布列,求离散型随机变量η=f(ξ)的分布列的关键是弄清楚ξ取每一个值时对应的η的值,再把η取相同的值时所对应的事件的概率相加,列出分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
1.将一颗骰子随机掷两次,下列选项中可以作为随机变量的是( )
A.第一次出现的点数 B.第二次出现的点数
C.两次出现点数之和 D.两次出现相同点的种数
解析:A,B中出现的点数虽然是随机的,但它们取值所反映的结果,都不是本题涉及试验的结果.C整体反映两次投掷的结果,可以预见两次出现数字的和是2,3,4,5,6,7,8,9,10,11,12,这11种结果,但每掷一次前,无法预见是11种中的哪一个,故是随机变量.D中出现相同点数的种数就是6种,不是变量.
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
2.袋中有大小相同的5个小球,分别标有1,2,3,4,5五个号码.在有放回地抽取条件下依次取出2个球,设两个球号码之和为随机变量ξ,则ξ所有可能取值的个数是( )
A.25 B.10
C.9 D.5
解析:第一次可取1,2,3,4,5中的任意一个,由于是有放回抽取,第二次也可取1,2,3,4,5中的任何一个,两次的号码和可能为2,3,4,5,6,7,8,9,10.
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.设X是一个离散型随机变量,其分布列为:
则q等于( )
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
4.随机变量η的分布列如下:
则x= ,P(η≤3)= .?
解析:由分布列的性质得0.2+x+0.25+0.1+0.15+0.2=1,解得x=0.1.故P(η≤3)=P(η=1)+P(η=2)+P(η=3)=0.1+0.2+0.25=0.55.
答案:0.1 0.55
5.随机变量ξ服从两点分布,且P(ξ=1)=0.8,η=3ξ-2,则P(η=-2)= .?
解析:当η=-2时,ξ=0,所以P(η=-2)=P(ξ=0)=1-P(ξ=1)=0.2.
答案:0.2
η
1
2
3
4
5
6
P
0.2
x
0.25
0.1
0.15
0.2
4.2.2 离散型随机变量的分布列
课标阐释
思维脉络
1.了解随机变量及其与事件的联系.
2.理解离散型随机变量的概念.
3.能写出离散型随机变量的可能取值,并能解释其意义.
4.理解离散型随机变量分布列的概念及性质,会求离散型随机变量的分布列.
5.理解两点分布的意义,能够利用两点分布解决实际问题.
激趣诱思
知识点拨
在射击比赛中,运动员射击一次,可能出现命中0环,命中1环,…,命中10环等结果,若用变量X来表示他一次射击所命中的环数,则变量X取值情况如何?(变量X的结果可能由0,1,…,10这11个数表示.)
激趣诱思
知识点拨
一、随机变量及其与事件的联系
1.随机变量
定义
一般地,如果随机试验的样本空间为Ω,而且对于Ω中的每一个样本点,变量X都对应有唯一确定的实数值,就称X为一个随机变量
表示
随机变量一般用大写英文字母X,Y,Z,…或小写希腊字母ξ,η,ζ,…表示
范围
随机变量所有可能的取值组成的集合,称为这个随机变量的取值范围
激趣诱思
知识点拨
2.随机变量与事件的联系
一般地,如果X是一个随机变量,a,b都是任意实数,那么X=a,X≤b,X>b等都表示事件,而且:
(1)当a≠b时,事件X=a与X=b互斥;
(2)事件X≤a与X>a相互对立,因此P(X≤a)+P(X>a)=1.
3.离散型随机变量
取值
特点
一一列出
对于随机变量所有可能取的值都能一一列举出来
有限性
离散型随机变量只取有限个值
激趣诱思
知识点拨
4.随机变量之间的关系
一般地,如果X是一个随机变量,a,b都是实数且a≠0,则Y=aX+b也是一个随机变量.
由于X=t的充要条件是Y=at+b,因此P(X=t)=P(Y=at+b).
名师点析 判断一个随机变量X是否为离散型随机变量的方法
(1)明确试验的所有可能结果;
(2)将随机试验的试验结果数量化;
(3)确定试验结果所对应的实数是否可按一定次序一一列出,如果能一一列举出来,那么该随机变量是离散型随机变量,否则不是.
激趣诱思
知识点拨
微思考1
若说随机变量就是函数,对吗?
提示:随机变量不一定为函数,函数是非空数集A,B间的一种对应,而随机变量间的对应是基本事件与实数间的对应.
微思考2
类似地,函数的定义域和值域相当于随机变量概念中的哪些量?
提示:随机变量与函数都是一种对应,试验结果的范围相当于函数的定义域,随机变量的取值范围相当于函数的值域.
微练习
若学校餐厅中午一共提供了1 000个馒头,则餐厅能卖出的馒头数X是否为随机变量?如果是,请写出它的取值.
解:是.X的所有可能取值为0,1,2,3,4,…,1 000.
激趣诱思
知识点拨
二、离散型随机变量的分布列
1.离散型随机变量的分布列
一般地,当离散型随机变量X的取值范围是{x1,x2,…,xn}时,如果对任意k∈{1,2,…,n},概率P(X=xk)=pk都是已知的,则称X的概率分布是已知的.离散型随机变量X的概率分布可以用如下形式的表格表示,这个表格称为X的概率分布或分布列.
X
x1
x2
…
xk
…
xn
P
p1
p2
…
pk
…
pn
离散型随机变量的分布列满足:
(1)pk≥0,k=1,2,…,n;
激趣诱思
知识点拨
名师点析 (1)离散型随机变量的分布列不仅能清楚地反映其所取的一切可能的值,而且也能清楚地看到取每一个值的概率的大小,从而反映了随机变量在随机试验中取值的分布状况,是进一步研究随机试验数量特征的基础.
(2)由于随机变量的各个可能取值之间彼此互斥,因此,随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.
(3)当X与Y都是离散型随机变量而且Y=aX+b(a≠0)时,X与Y的分布列分别如下表所示,它们的第二行的概率值是一样的.
X
x1
x2
…
xk
…
xn
P
p1
p2
…
pk
…
pn
Y=aX+b
ax1+b
ax2+b
…
axk+b
…
axn+b
P
p1
p2
…
pk
…
pn
激趣诱思
知识点拨
2.两点分布
一般地,如果随机变量X的分布列为
其中0
(2)两点分布的试验结果只有两个可能,且概率之和为1.
X
1
0
P
p
1-p
激趣诱思
知识点拨
微思考
如何根据定义求一个随机变量的分布列?
提示:其步骤为:①设出随机变量X,并确定X的所有可能取值,以及取每个值的意义;②计算X取每个值的概率;③写出X的分布列(一般列表).
激趣诱思
知识点拨
微练习1
下列表中可以作为离散型随机变量的分布列是( )
答案:D
激趣诱思
知识点拨
微练习2
X
0
1
P
?
?
探究一
探究二
探究三
探究四
素养形成
当堂检测
随机变量的可能取值及试验结果
例1写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果.
(1)一个袋中装有8个红球,3个白球,从中任取5个球,其中所含白球的个数为X.
(2)一个袋中有5个同样大小的黑球,编号为1,2,3,4,5,从中任取3个球,取出的球的最大号码记为X.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:(1)X=0表示取5个球全是红球;
X=1表示取1个白球,4个红球;
X=2表示取2个白球,3个红球;
X=3表示取3个白球,2个红球.
(2)X=3表示取出的球编号为1,2,3.
X=4表示取出的球编号为1,2,4;1,3,4或2,3,4.
X=5表示取出的球编号为1,2,5;1,3,5;1,4,5;2,3,5;2,4,5或3,4,5.
反思感悟 用随机变量表示随机试验的结果的关键点和注意点
(1)关键点:解决此类问题的关键是明确随机变量的所有可能取值,以及取每一个值对应的意义,即一个随机变量的取值对应一个或多个随机试验的结果.
(2)注意点:解答过程中不要漏掉某些试验结果.
探究一
探究二
探究三
探究四
素养形成
当堂检测
延伸探究 在本例(1)条件下,规定取出一个红球得2分,而每取出一个白球减1分,以ξ表示得的分数,结果如何?
解:ξ=10表示取5个球全是红球;
ξ=7表示取1个白球,4个红球;
ξ=4表示取2个白球,3个红球;
ξ=1表示取3个白球,2个红球.
探究一
探究二
探究三
探究四
素养形成
当堂检测
求离散型随机变量的分布列
例2一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的3只球中的最大号码,写出随机变量ξ的分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 求离散型随机变量分布列时应注意的问题
(1)确定离散型随机变量ξ的分布列的关键是要清楚ξ取每一个值对应的随机事件,进一步利用排列、组合知识求出ξ取每一个值的概率.
(2)在求离散型随机变量ξ的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可以验证分布列是否正确.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1某班有学生45人,其中是O型血的有10人,A型血的有12人,B型血的有8人,AB型血的有15人.现从中抽1人,其血型为随机变量X,求X的分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
离散型随机变量分布列的性质
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 利用离散型分布列的性质解题时要注意以下两个问题
(1)X=Xi(i=1,2,…,n)的各个取值表示的事件是互斥的.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练2若离散型随机变量X的分布列为
求常数a及相应的分布列.
X
0
1
P
4a-1
3a2+a
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
两点分布
例4已知一批200件的待出厂产品中,有1件不合格品,现从中任意抽取2件进行检查,若用随机变量X表示抽取的2件产品中的次品数,求X的分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 两点分布的4个特点
(1)两点分布中只有两个对应结果,且两结果是对立的;
(2)两点分布中的两个结果一个对应1,另一个对应0;
(3)由互斥事件的概率求法可知,已知P(X=0)(或P(X=1)),便可求出P(X=1)(或P(X=0)).
(4)在有多个结果的随机试验中,如果我们只关心一个随机事件是否发生,就可以利用两点分布来研究它.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练3设某项试验的成功率是失败率的2倍,用随机变量X描述一次试验的成功次数,则P(X=0)等于( )
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
求离散型随机变量y=f(ξ)的分布列
典例 设离散型随机变量X的分布列为
求:(1)2X+1的分布列;
(2)|X-1|的分布列.
X
0
1
2
3
4
P
0.2
0.1
0.1
0.3
m
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:由分布列的性质知0.2+0.1+0.1+0.3+m=1,
解得m=0.3.
首先列表为
从而由上表得两个分布列为
(1)2X+1的分布列
(2)|X-1|的分布列
X
0
1
2
3
4
2X+1
1
3
5
7
9
|X-1|
1
0
1
2
3
2X+1
1
3
5
7
9
P
0.2
0.1
0.1
0.3
0.3
|X-1|
0
1
2
3
P
0.1
0.3
0.3
0.3
探究一
探究二
探究三
探究四
素养形成
当堂检测
方法点睛 (1)若ξ是一个随机变量,a,b是常数,且a≠0,则η=aξ+b也是一个随机变量,推广到一般情况有:若ξ是随机变量,f(ξ)是连续函数或单调函数,则η=f(ξ)也是随机变量,也就是说,随机变量的某些函数值也是随机变量,并且若ξ为离散型随机变量,则η=f(ξ)也为离散型随机变量.
(2)已知离散型随机变量ξ的分布列,求离散型随机变量η=f(ξ)的分布列的关键是弄清楚ξ取每一个值时对应的η的值,再把η取相同的值时所对应的事件的概率相加,列出分布列.
探究一
探究二
探究三
探究四
素养形成
当堂检测
1.将一颗骰子随机掷两次,下列选项中可以作为随机变量的是( )
A.第一次出现的点数 B.第二次出现的点数
C.两次出现点数之和 D.两次出现相同点的种数
解析:A,B中出现的点数虽然是随机的,但它们取值所反映的结果,都不是本题涉及试验的结果.C整体反映两次投掷的结果,可以预见两次出现数字的和是2,3,4,5,6,7,8,9,10,11,12,这11种结果,但每掷一次前,无法预见是11种中的哪一个,故是随机变量.D中出现相同点数的种数就是6种,不是变量.
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
2.袋中有大小相同的5个小球,分别标有1,2,3,4,5五个号码.在有放回地抽取条件下依次取出2个球,设两个球号码之和为随机变量ξ,则ξ所有可能取值的个数是( )
A.25 B.10
C.9 D.5
解析:第一次可取1,2,3,4,5中的任意一个,由于是有放回抽取,第二次也可取1,2,3,4,5中的任何一个,两次的号码和可能为2,3,4,5,6,7,8,9,10.
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.设X是一个离散型随机变量,其分布列为:
则q等于( )
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
4.随机变量η的分布列如下:
则x= ,P(η≤3)= .?
解析:由分布列的性质得0.2+x+0.25+0.1+0.15+0.2=1,解得x=0.1.故P(η≤3)=P(η=1)+P(η=2)+P(η=3)=0.1+0.2+0.25=0.55.
答案:0.1 0.55
5.随机变量ξ服从两点分布,且P(ξ=1)=0.8,η=3ξ-2,则P(η=-2)= .?
解析:当η=-2时,ξ=0,所以P(η=-2)=P(ξ=0)=1-P(ξ=1)=0.2.
答案:0.2
η
1
2
3
4
5
6
P
0.2
x
0.25
0.1
0.15
0.2
