人教B版(2019)高中数学选择性必修第二册 4.2.4 第一课时 离散型随机变量的均值(共34张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第二册 4.2.4 第一课时 离散型随机变量的均值(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 11:39:30 | ||
图片预览











文档简介
第一课时 离散型随机变量的均值
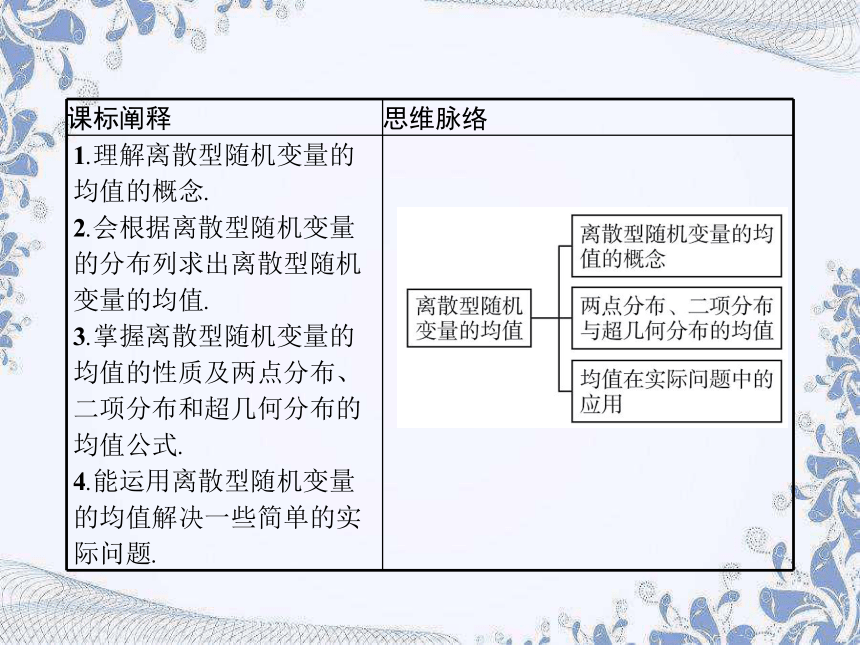
课标阐释
思维脉络
1.理解离散型随机变量的均值的概念.
2.会根据离散型随机变量的分布列求出离散型随机变量的均值.
3.掌握离散型随机变量的均值的性质及两点分布、二项分布和超几何分布的均值公式.
4.能运用离散型随机变量的均值解决一些简单的实际问题.
激趣诱思
知识点拨
某城市随机抽样调查了1 000户居民的住房情况,发现户型主要集中于160 m2,100 m2,60 m2三种,对应住房的比例为1∶5∶4,能否说该市的人均住房面积为
此种计算显然不合理,忽略了不同住房面积的居民所占的比例,造成了“被平均”现象.那么如何计算人均住房面积更为合理呢?通过本节的学习,我们就会得到答案.
激趣诱思
知识点拨
一、均值
一般地,如果离散型随机变量X的分布列如下表所示.
激趣诱思
知识点拨
名师点析 (1)均值E(X)刻画的是X取值的“中心位置”,这是随机变量X的一个重要特征,它反映或刻画的是随机变量取值的平均水平.由定义可知离散型随机变量的均值与它的本身有相同的单位.
(2)随机变量的均值与样本平均值的关系:
随机变量的均值是一个常数,它不依赖于样本的抽取,而样本的平均值是一个随机变量,它随样本的抽取的不同而变化.对于简单随机抽样,随着样本容量的增加,样本平均值越来越接近于总体的均值.随机变量X的均值反映了离散型随机变量的平均水平.
激趣诱思
知识点拨
微拓展
离散型随机变量的均值的性质
若X,Y是两个随机变量,且Y=aX+b,则有E(Y)=aE(X)+b,即随机变量X的线性函数的均值等于这个随机变量的均值E(X)的同一线性函数.特别地:
(1)当a=0时,E(b)=b,即常数的均值就是这个常数本身.
(2)当a=1时,E(X+b)=E(X)+b,即随机变量X与常数之和的均值等于X的均值与这个常数的和.
(3)当b=0时,E(aX)=aE(X),即常数与随机变量乘积的均值等于这个常数与随机变量的均值的乘积.
激趣诱思
知识点拨
微练习
掷一枚质地均匀的骰子n次,用X表示出现的点数.求离散型随机变量X的分布列和均值.
激趣诱思
知识点拨
二、常见的均值
1.若离散型随机变量X服从参数为p的两点分布,则E(X)=p.
2.若离散型随机变量X服从参数为n和p的二项分布,即X~B(n,p),则E(X)=np.
3.若离散型随机变量X服从参数为N,n,M的超几何分布,即X~H(N,n,M),则E(X)= .
激趣诱思
知识点拨
微练习
篮球运动员在比赛中每次罚球命中得1分,罚球不中得0分.已知某运动员罚球命中的概率为0.7,求他罚球1次的得分X的均值.
解:X的可能值为0,1.P(X=0)=1-0.7=0.3,P(X=1)=0.7.故X的分布列为
所以E(X)=1×0.7+0×0.3=0.7.
X
1
0
P
0.7
0.3
探究一
探究二
探究三
素养形成
当堂检测
求离散型随机变量的均值
例1某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样.购买一瓶,若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料.
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及均值E(ξ).
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 求离散型随机变量的均值的步骤
(1)确定取值:根据随机变量X的意义,写出X可能取得的全部值;
(2)求概率:求X取每个值的概率;
(3)写分布列:写出X的分布列;
(4)求均值:由均值的定义求出E(X).
其中准确写出随机变量的分布列是求解此类问题的关键.
探究一
探究二
探究三
素养形成
当堂检测
(1)求X的分布列;
(2)求X和Y的均值.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
离散型随机变量均值的性质
例2已知随机变量X的分布列为
若Y=-2X,则E(Y)= .?
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 与离散型随机变量性质有关问题的解题思路
若给出的随机变量ξ与X的关系为ξ=aX+b,a,b为常数.一般思路是先求出E(X),再利用公式E(aX+b)=aE(X)+b求E(ξ).也可以利用X的分布列得到ξ的分布列,由X的取值计算ξ的取值,对应的概率相等,再由定义法求得E(ξ).
探究一
探究二
探究三
素养形成
当堂检测
延伸探究 本例条件不变,若Y=2X-3,求E(Y).
探究一
探究二
探究三
素养形成
当堂检测
均值的实际应用
例3某商场经销某商品,根据以往资料统计,顾客采用的付款期数ξ的分布列为
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(1)求事件A“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
(2)求η的分布列及均值E(η).
ξ
1
2
3
4
5
P
0.4
0.2
0.2
0.1
0.1
探究一
探究二
探究三
素养形成
当堂检测
解:(1)由A表示事件“购买该商品的3位顾客中至少有1位采用1期付款”知, 表示事件“购买该商品的3位顾客中无人采用1期付款”.
(2)η的可能取值为200元,250元,300元.
P(η=200)=P(ξ=1)=0.4,
P(η=250)=P(ξ=2)+P(ξ=3)=0.2+0.2=0.4,
P(η=300)=P(ξ=4)+P(ξ=5)=0.1+0.1=0.2,
因此η的分布列为
E(η)=200×0.4+250×0.4+300×0.2=240(元).
η
200
250
300
P
0.4
0.4
0.2
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.实际问题中的均值问题
均值在实际中有着广泛的应用,如在体育比赛的安排和成绩预测、消费预测、工程方案的预测、产品合格率的预测、投资收益等,都可以通过随机变量的均值来进行估计.
2.概率模型的解答步骤
(1)审题,确定实际问题是哪一种概率模型,可能用到的事件类型,所用的公式有哪些.
(2)确定随机变量的分布列,计算随机变量的均值.
(3)对照实际意义,回答概率、均值等所表示的结论.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
特殊分布的数学期望
(1)两种大树各成活1棵的概率;
(2)成活的棵数ξ的分布列与数学期望.
分析本题主要考查独立重复试验和分布列的应用,求解时可由二项分布求数学期望.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
方法点睛 解决此类问题,首先应依据二项分布、两点分布及超几何分布的特点,判断随机变量属于哪一种分布,再写出随机变量的分布列,然后利用数学期望公式求解.
探究一
探究二
探究三
素养形成
当堂检测
1.已知随机变量X的分布列如下表,随机变量X的数学期望E(X)=1,则x的值为( )
A.0.3 B.0.24 C.0.4 D.0.2
X
0
1
2
P
0.4
x
y
答案:D
探究一
探究二
探究三
素养形成
当堂检测
2.某射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目X的数学期望为( )
A.2.44 B.3.376
C.2.376 D.2.4
解析:X的可能取值为3,2,1,0,P(X=3)=0.6;
P(X=2)=0.4×0.6=0.24;
P(X=1)=0.42×0.6=0.096;
P(X=0)=0.43=0.064.
所以E(X)=3×0.6+2×0.24+1×0.096+0×0.064=2.376.
答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.已知ξ的分布列如下表,若η=3ξ+2,则E(η)= .?
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
5.口袋里装有大小相同的8张卡片,其中3张标有数字1,3张标有数字2,2张标有数字3.第一次从口袋里任意抽取1张,放回口袋里后第二次再任意抽取1张,记第一次与第二次取到卡片上数字之和为ξ.求:
(1)ξ为何值时,其发生的概率最大?并说明理由.
(2)随机变量ξ的数学期望E(ξ).
探究一
探究二
探究三
素养形成
当堂检测
课标阐释
思维脉络
1.理解离散型随机变量的均值的概念.
2.会根据离散型随机变量的分布列求出离散型随机变量的均值.
3.掌握离散型随机变量的均值的性质及两点分布、二项分布和超几何分布的均值公式.
4.能运用离散型随机变量的均值解决一些简单的实际问题.
激趣诱思
知识点拨
某城市随机抽样调查了1 000户居民的住房情况,发现户型主要集中于160 m2,100 m2,60 m2三种,对应住房的比例为1∶5∶4,能否说该市的人均住房面积为
此种计算显然不合理,忽略了不同住房面积的居民所占的比例,造成了“被平均”现象.那么如何计算人均住房面积更为合理呢?通过本节的学习,我们就会得到答案.
激趣诱思
知识点拨
一、均值
一般地,如果离散型随机变量X的分布列如下表所示.
激趣诱思
知识点拨
名师点析 (1)均值E(X)刻画的是X取值的“中心位置”,这是随机变量X的一个重要特征,它反映或刻画的是随机变量取值的平均水平.由定义可知离散型随机变量的均值与它的本身有相同的单位.
(2)随机变量的均值与样本平均值的关系:
随机变量的均值是一个常数,它不依赖于样本的抽取,而样本的平均值是一个随机变量,它随样本的抽取的不同而变化.对于简单随机抽样,随着样本容量的增加,样本平均值越来越接近于总体的均值.随机变量X的均值反映了离散型随机变量的平均水平.
激趣诱思
知识点拨
微拓展
离散型随机变量的均值的性质
若X,Y是两个随机变量,且Y=aX+b,则有E(Y)=aE(X)+b,即随机变量X的线性函数的均值等于这个随机变量的均值E(X)的同一线性函数.特别地:
(1)当a=0时,E(b)=b,即常数的均值就是这个常数本身.
(2)当a=1时,E(X+b)=E(X)+b,即随机变量X与常数之和的均值等于X的均值与这个常数的和.
(3)当b=0时,E(aX)=aE(X),即常数与随机变量乘积的均值等于这个常数与随机变量的均值的乘积.
激趣诱思
知识点拨
微练习
掷一枚质地均匀的骰子n次,用X表示出现的点数.求离散型随机变量X的分布列和均值.
激趣诱思
知识点拨
二、常见的均值
1.若离散型随机变量X服从参数为p的两点分布,则E(X)=p.
2.若离散型随机变量X服从参数为n和p的二项分布,即X~B(n,p),则E(X)=np.
3.若离散型随机变量X服从参数为N,n,M的超几何分布,即X~H(N,n,M),则E(X)= .
激趣诱思
知识点拨
微练习
篮球运动员在比赛中每次罚球命中得1分,罚球不中得0分.已知某运动员罚球命中的概率为0.7,求他罚球1次的得分X的均值.
解:X的可能值为0,1.P(X=0)=1-0.7=0.3,P(X=1)=0.7.故X的分布列为
所以E(X)=1×0.7+0×0.3=0.7.
X
1
0
P
0.7
0.3
探究一
探究二
探究三
素养形成
当堂检测
求离散型随机变量的均值
例1某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样.购买一瓶,若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料.
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及均值E(ξ).
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 求离散型随机变量的均值的步骤
(1)确定取值:根据随机变量X的意义,写出X可能取得的全部值;
(2)求概率:求X取每个值的概率;
(3)写分布列:写出X的分布列;
(4)求均值:由均值的定义求出E(X).
其中准确写出随机变量的分布列是求解此类问题的关键.
探究一
探究二
探究三
素养形成
当堂检测
(1)求X的分布列;
(2)求X和Y的均值.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
离散型随机变量均值的性质
例2已知随机变量X的分布列为
若Y=-2X,则E(Y)= .?
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 与离散型随机变量性质有关问题的解题思路
若给出的随机变量ξ与X的关系为ξ=aX+b,a,b为常数.一般思路是先求出E(X),再利用公式E(aX+b)=aE(X)+b求E(ξ).也可以利用X的分布列得到ξ的分布列,由X的取值计算ξ的取值,对应的概率相等,再由定义法求得E(ξ).
探究一
探究二
探究三
素养形成
当堂检测
延伸探究 本例条件不变,若Y=2X-3,求E(Y).
探究一
探究二
探究三
素养形成
当堂检测
均值的实际应用
例3某商场经销某商品,根据以往资料统计,顾客采用的付款期数ξ的分布列为
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(1)求事件A“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
(2)求η的分布列及均值E(η).
ξ
1
2
3
4
5
P
0.4
0.2
0.2
0.1
0.1
探究一
探究二
探究三
素养形成
当堂检测
解:(1)由A表示事件“购买该商品的3位顾客中至少有1位采用1期付款”知, 表示事件“购买该商品的3位顾客中无人采用1期付款”.
(2)η的可能取值为200元,250元,300元.
P(η=200)=P(ξ=1)=0.4,
P(η=250)=P(ξ=2)+P(ξ=3)=0.2+0.2=0.4,
P(η=300)=P(ξ=4)+P(ξ=5)=0.1+0.1=0.2,
因此η的分布列为
E(η)=200×0.4+250×0.4+300×0.2=240(元).
η
200
250
300
P
0.4
0.4
0.2
探究一
探究二
探究三
素养形成
当堂检测
反思感悟 1.实际问题中的均值问题
均值在实际中有着广泛的应用,如在体育比赛的安排和成绩预测、消费预测、工程方案的预测、产品合格率的预测、投资收益等,都可以通过随机变量的均值来进行估计.
2.概率模型的解答步骤
(1)审题,确定实际问题是哪一种概率模型,可能用到的事件类型,所用的公式有哪些.
(2)确定随机变量的分布列,计算随机变量的均值.
(3)对照实际意义,回答概率、均值等所表示的结论.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
特殊分布的数学期望
(1)两种大树各成活1棵的概率;
(2)成活的棵数ξ的分布列与数学期望.
分析本题主要考查独立重复试验和分布列的应用,求解时可由二项分布求数学期望.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
方法点睛 解决此类问题,首先应依据二项分布、两点分布及超几何分布的特点,判断随机变量属于哪一种分布,再写出随机变量的分布列,然后利用数学期望公式求解.
探究一
探究二
探究三
素养形成
当堂检测
1.已知随机变量X的分布列如下表,随机变量X的数学期望E(X)=1,则x的值为( )
A.0.3 B.0.24 C.0.4 D.0.2
X
0
1
2
P
0.4
x
y
答案:D
探究一
探究二
探究三
素养形成
当堂检测
2.某射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目X的数学期望为( )
A.2.44 B.3.376
C.2.376 D.2.4
解析:X的可能取值为3,2,1,0,P(X=3)=0.6;
P(X=2)=0.4×0.6=0.24;
P(X=1)=0.42×0.6=0.096;
P(X=0)=0.43=0.064.
所以E(X)=3×0.6+2×0.24+1×0.096+0×0.064=2.376.
答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.已知ξ的分布列如下表,若η=3ξ+2,则E(η)= .?
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
5.口袋里装有大小相同的8张卡片,其中3张标有数字1,3张标有数字2,2张标有数字3.第一次从口袋里任意抽取1张,放回口袋里后第二次再任意抽取1张,记第一次与第二次取到卡片上数字之和为ξ.求:
(1)ξ为何值时,其发生的概率最大?并说明理由.
(2)随机变量ξ的数学期望E(ξ).
探究一
探究二
探究三
素养形成
当堂检测
