人教B版(2019)高中数学选择性必修第二册 4.3.2 独立性检验(共29张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第二册 4.3.2 独立性检验(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 708.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览







文档简介
4.3.2 独立性检验
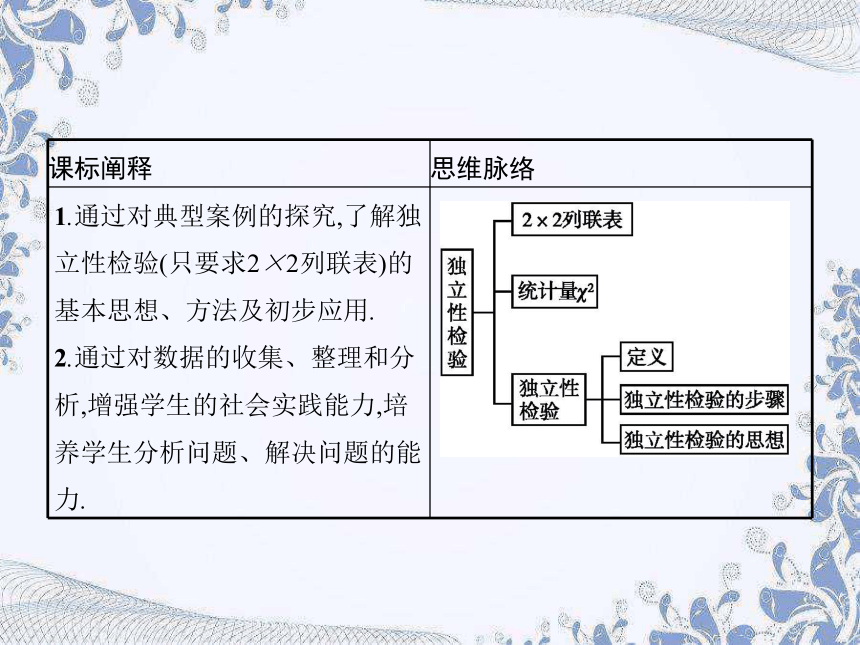
课标阐释
思维脉络
1.通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用.
2.通过对数据的收集、整理和分析,增强学生的社会实践能力,培养学生分析问题、解决问题的能力.
激趣诱思
知识点拨
我国相关法律规定:香烟盒上必须印上“吸烟有害健康”的警示语.那么吸烟和健康之间有因果关系吗?每一个吸烟者的健康问题都是由吸烟引起的吗?你认为“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法对吗?要回答这个问题,我们先一起来学习本课时的知识吧!
激趣诱思
知识点拨
独立性检验
1.如果随机事件A与B的样本数据的2×2列联表如下:
记n=a+b+c+d.统计学中有一个非常有用的统计量χ2(读作“卡方”).
?
A
?
总计
B
a
b
a+b
?
c
d
c+d
总计
a+c
b+d
a+b+c+d
激趣诱思
知识点拨
2.任意给定一个α(称为显著性水平,通常取为0.05,0.01等),可以找到满足条件P(χ2≥k)=α的数k(称为显著性水平α对应的分位数).χ2是一个随机变量,其分布能够求出,上面的概率是可以计算的.因此,如果根据样本数据算出χ2的值后,发现χ2≥k成立,就称在犯错误的概率不超过α的前提下,可以认为A与B不独立(也称为A与B有关);或说有1-α的把握认为A与B有关.若χ2 3.A与B独立时,也称为A与B无关.当χ2激趣诱思
知识点拨
4.独立性的判断方法
(1)当χ2<2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
(2)当χ2≥2.706时,有90%的把握判定变量A,B有关联;
(3)当χ2≥3.841时,有95%的把握判定变量A,B有关联;
(4)当χ2≥6.635时,有99%的把握判定变量A,B有关联.
激趣诱思
知识点拨
名师点析 独立性检验的思想来自统计上的假设检验思想,它与反证法类似,假设检验和反证法都是先假设不成立,然后根据是否能推出“矛盾”来判断是否成立,但二者“矛盾”的含义不同,反证法中的“矛盾”是指不符合逻辑的事件发生,而假设检验中的“矛盾”是指不符合逻辑的小概率事件发生.小概率事件在一次试验中通常是不会发生的,如果在假设“两个变量无关系”的前提下这个小概率事件发生,这只能说明假设不成立,所以认为原结论在很大程度上是成立的.
激趣诱思
知识点拨
微思考
独立性检验的结论是不是适用于总体中的所有个体?
提示:独立性检验的结论与实际问题的差异:独立性检验的结论是一个数学统计量,是用样本来估计总体,虽然能较为真实地反映出总体的情况,但它与实际问题的确定性是允许存在差异的,因为实质上它是一种统计关系,而不是一个确定的关系,我们不能期望所得的结论对于总体中的每一个个体都适用.
激趣诱思
知识点拨
微练习
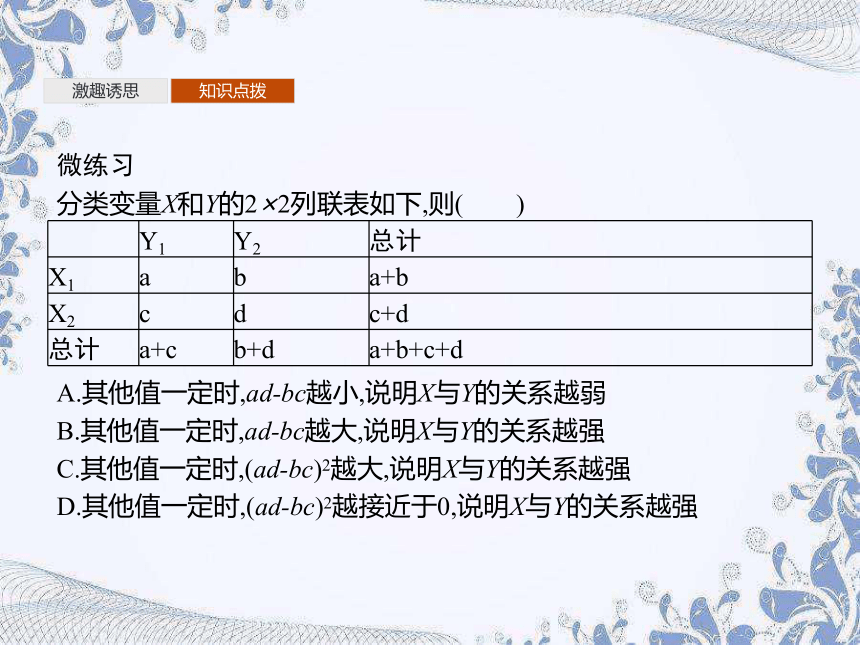
分类变量X和Y的2×2列联表如下,则( )
A.其他值一定时,ad-bc越小,说明X与Y的关系越弱
B.其他值一定时,ad-bc越大,说明X与Y的关系越强
C.其他值一定时,(ad-bc)2越大,说明X与Y的关系越强
D.其他值一定时,(ad-bc)2越接近于0,说明X与Y的关系越强
?
Y1
Y2
总计
X1
a
b
a+b
X2
c
d
c+d
总计
a+c
b+d
a+b+c+d
激趣诱思
知识点拨
解析:由 可知,其他值一定的情况下,(ad-bc)2越大,则χ2的值越大,则X与Y的关系越强,故选C.
答案:C
探究一
探究二
素养形成
当堂检测
由χ2进行独立性检验
例1某校高三年级举行一次全年级的大型考试,在数学成绩优秀和非优秀的学生中,物理、化学也为优秀的人数如下表所示,则我们能否在犯错误的概率不超过0.001 的前提下认为数学成绩优秀与物理、化学优秀有关系?
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
分析首先分别列出数学成绩与物理、化学的2×2列联表,再正确计算χ2的值,然后由χ2的值和临界值比较作出判断.
?
物理优秀
化学优秀
数学优秀
228
225
数学非优秀
143
156
探究一
探究二
素养形成
当堂检测
解:根据已知数据列出数学与物理优秀的2×2列联表如下:
?
物理优秀
物理非优秀
总计
数学优秀
228
b1
360
数学非优秀
143
d1
880
总计
371
b1+d1
1 240
∴b1=360-228=132,d1=880-143=737,b1+d1=132+737=869.
代入公式可得χ2≈270.114.
按照上述方法列出数学与化学优秀的2×2列联表如下:
探究一
探究二
素养形成
当堂检测
?
化学优秀
化学非优秀
总计
数学优秀
225
b2
360
数学非优秀
156
d2
880
总计
381
b2+d2
1 240
∴b2=360-225=135,d2=880-156=724,b2+d2=135+724=859.
代入公式可得χ2≈240.611.
综上,由于χ2的值都大于10.828,因此说明都能在犯错误的概率不超过0.001的前提下认为数学成绩优秀与物理、化学优秀有关系.
探究一
探究二
素养形成
当堂检测
反思感悟 1.利用χ2进行独立性检验的步骤
(1)列表:列出2×2列联表;
(2)求值:求出χ2;
(3)判断:与临界值比较,作出判断.
2.独立性检验的必要性
列联表中的数据是样本数据,它只是总体的代表,它具有随机性,所以只能利用列联表的数据和等高条形图粗略判断两个分类变量是否有关系.而χ2给出了不同样本容量的数据的统一评判标准.利用它能精确判断两个分类变量是否有关系的可靠程度.
探究一
探究二
素养形成
当堂检测
变式训练为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下,认为“学生选报文、理科与对外语的兴趣有关”?
探究一
探究二
素养形成
当堂检测
解:根据题目所给的数据得到如下列联表:
根据列联表中数据由公式计算得随机变量的观测值
因为1.871×10-4<2.706,所以在犯错误的概率不超过0.1的前提下,不能认为“学生选报文、理科与对外语的兴趣有关”.
?
理科
文科
总计
有兴趣
138
73
211
无兴趣
98
52
150
总计
236
125
361
探究一
探究二
素养形成
当堂检测
独立性检验与统计的综合应用
例2为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)表1和表2分别是注射药物A和B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表
疱疹面积
[60,65)
[65,70)
[70,75)
[75,80)
频数
30
40
20
10
探究一
探究二
素养形成
当堂检测
表2:注射药物B后皮肤疱疹面积的频数分布表
完成下面2×2列联表
疱疹面积
[60,65)
[65,70)
[70,75)
[75,80)
[80,85]
频数
10
25
20
30
15
?
疱疹面积小于
70 mm2
疱疹面积不小于
70 mm2
总计
注射药物A
a=
b=
?
注射药物B
c=
d=
?
总计
?
?
n=
探究一
探究二
素养形成
当堂检测
(2)2×2列联表如下
?
疱疹面积小于
70 mm2
疱疹面积不小于
70 mm2
总计
注射药物A
a=70
b=30
100
注射药物B
c=35
d=65
100
总计
105
95
n=200
探究一
探究二
素养形成
当堂检测
反思感悟 1.独立性检验在实际中有着广泛的应用,是对实际生活中数据进行分析的一种方法,通过这种分析得出的结论对实际生活或者生产都有一定的指导作用.
2.近几年高考中较少单独考查独立性检验,经常与统计、概率等知识综合,频率分布表、频率分布直方图与独立性检验融合在一起是常见的考查形式,一般需要根据条件列出2×2列联表,计算χ2,从而解决问题.
探究一
探究二
素养形成
当堂检测
延伸探究 本例条件不变,是否有99%的把握认为注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异?
由于χ2>6.635,所以有99%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
探究一
探究二
素养形成
当堂检测
规范解答
典例 随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康情况,得到2×2列联表如下:
?
室外工作
室内工作
总计
有呼吸系统疾病
150
?
?
无呼吸系统疾病
?
100
?
总 计
200
?
?
探究一
探究二
素养形成
当堂检测
(1)补全2×2列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关?
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机地抽取两人,求两人都有呼吸系统疾病的概率.
探究一
探究二
素养形成
当堂检测
解:(1)列联表如下:
所以能在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关.
?
室外工作
室内工作
总计
有呼吸系统疾病
150
200
350
无呼吸系统疾病
50
100
150
总 计
200
300
500
探究一
探究二
素养形成
当堂检测
(3)采用分层抽样从室内工作的居民中抽取6名,其中有呼吸系统疾病的抽4人,无呼吸系统疾病的抽2人,设A为“从中随机地抽取两人,两人都有呼吸系统疾病”,则
方法点睛 (1)依题意补全列联表;(2)结合χ2公式正确求解,对说法作出判断;(3)结合概率相关知识求解.
探究一
探究二
素养形成
当堂检测
1.给出下列实际问题:
①一种药物对某种病的治愈率;②两种药物治疗同一种病是否有区别;③吸烟者得肺病的概率;④吸烟是否与性别有关系;⑤网吧与青少年的犯罪是否有关系.其中用独立性检验可以解决的问题有( )
A.①②③ B.②④⑤
C.②③④⑤ D.①②③④⑤
解析:独立性检验是判断两个分类变量是否有关系的方法,而①③都是概率问题,不能用独立性检验解决.
答案:B
探究一
探究二
素养形成
当堂检测
2.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
下列叙述中,正确的是( )
A.有99%的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”
B.有95%的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”
C.有99%的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”
D.有95%的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”
答案:D
?
认为作业多
认为作业不多
总数
喜欢玩电脑游戏
18
9
27
不喜欢玩电脑游戏
8
15
23
总数
26
24
50
探究一
探究二
素养形成
当堂检测
3.某高校《统计》课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
?
为了判断主修统计专业是否与性别有关系,根据表中的数据,得到
因为4.844>3.841,所以有 的把握判定主修统计专业与性别有关系.?
答案:95%
专业
性别
非统计专业
统计专业
男
13
10
女
7
20
探究一
探究二
素养形成
当堂检测
4.调查者通过询问72名男、女大学生在购买食品时是否看营养说明得到的数据如下表所示:
大学生的性别和是否看营养说明之间 (填“有”或“没有”)关系.?
答案:有
?
看营养说明
不看营养说明
总计
男大学生
28
8
36
女大学生
16
20
36
总计
44
28
72
课标阐释
思维脉络
1.通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用.
2.通过对数据的收集、整理和分析,增强学生的社会实践能力,培养学生分析问题、解决问题的能力.
激趣诱思
知识点拨
我国相关法律规定:香烟盒上必须印上“吸烟有害健康”的警示语.那么吸烟和健康之间有因果关系吗?每一个吸烟者的健康问题都是由吸烟引起的吗?你认为“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法对吗?要回答这个问题,我们先一起来学习本课时的知识吧!
激趣诱思
知识点拨
独立性检验
1.如果随机事件A与B的样本数据的2×2列联表如下:
记n=a+b+c+d.统计学中有一个非常有用的统计量χ2(读作“卡方”).
?
A
?
总计
B
a
b
a+b
?
c
d
c+d
总计
a+c
b+d
a+b+c+d
激趣诱思
知识点拨
2.任意给定一个α(称为显著性水平,通常取为0.05,0.01等),可以找到满足条件P(χ2≥k)=α的数k(称为显著性水平α对应的分位数).χ2是一个随机变量,其分布能够求出,上面的概率是可以计算的.因此,如果根据样本数据算出χ2的值后,发现χ2≥k成立,就称在犯错误的概率不超过α的前提下,可以认为A与B不独立(也称为A与B有关);或说有1-α的把握认为A与B有关.若χ2
知识点拨
4.独立性的判断方法
(1)当χ2<2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
(2)当χ2≥2.706时,有90%的把握判定变量A,B有关联;
(3)当χ2≥3.841时,有95%的把握判定变量A,B有关联;
(4)当χ2≥6.635时,有99%的把握判定变量A,B有关联.
激趣诱思
知识点拨
名师点析 独立性检验的思想来自统计上的假设检验思想,它与反证法类似,假设检验和反证法都是先假设不成立,然后根据是否能推出“矛盾”来判断是否成立,但二者“矛盾”的含义不同,反证法中的“矛盾”是指不符合逻辑的事件发生,而假设检验中的“矛盾”是指不符合逻辑的小概率事件发生.小概率事件在一次试验中通常是不会发生的,如果在假设“两个变量无关系”的前提下这个小概率事件发生,这只能说明假设不成立,所以认为原结论在很大程度上是成立的.
激趣诱思
知识点拨
微思考
独立性检验的结论是不是适用于总体中的所有个体?
提示:独立性检验的结论与实际问题的差异:独立性检验的结论是一个数学统计量,是用样本来估计总体,虽然能较为真实地反映出总体的情况,但它与实际问题的确定性是允许存在差异的,因为实质上它是一种统计关系,而不是一个确定的关系,我们不能期望所得的结论对于总体中的每一个个体都适用.
激趣诱思
知识点拨
微练习
分类变量X和Y的2×2列联表如下,则( )
A.其他值一定时,ad-bc越小,说明X与Y的关系越弱
B.其他值一定时,ad-bc越大,说明X与Y的关系越强
C.其他值一定时,(ad-bc)2越大,说明X与Y的关系越强
D.其他值一定时,(ad-bc)2越接近于0,说明X与Y的关系越强
?
Y1
Y2
总计
X1
a
b
a+b
X2
c
d
c+d
总计
a+c
b+d
a+b+c+d
激趣诱思
知识点拨
解析:由 可知,其他值一定的情况下,(ad-bc)2越大,则χ2的值越大,则X与Y的关系越强,故选C.
答案:C
探究一
探究二
素养形成
当堂检测
由χ2进行独立性检验
例1某校高三年级举行一次全年级的大型考试,在数学成绩优秀和非优秀的学生中,物理、化学也为优秀的人数如下表所示,则我们能否在犯错误的概率不超过0.001 的前提下认为数学成绩优秀与物理、化学优秀有关系?
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
分析首先分别列出数学成绩与物理、化学的2×2列联表,再正确计算χ2的值,然后由χ2的值和临界值比较作出判断.
?
物理优秀
化学优秀
数学优秀
228
225
数学非优秀
143
156
探究一
探究二
素养形成
当堂检测
解:根据已知数据列出数学与物理优秀的2×2列联表如下:
?
物理优秀
物理非优秀
总计
数学优秀
228
b1
360
数学非优秀
143
d1
880
总计
371
b1+d1
1 240
∴b1=360-228=132,d1=880-143=737,b1+d1=132+737=869.
代入公式可得χ2≈270.114.
按照上述方法列出数学与化学优秀的2×2列联表如下:
探究一
探究二
素养形成
当堂检测
?
化学优秀
化学非优秀
总计
数学优秀
225
b2
360
数学非优秀
156
d2
880
总计
381
b2+d2
1 240
∴b2=360-225=135,d2=880-156=724,b2+d2=135+724=859.
代入公式可得χ2≈240.611.
综上,由于χ2的值都大于10.828,因此说明都能在犯错误的概率不超过0.001的前提下认为数学成绩优秀与物理、化学优秀有关系.
探究一
探究二
素养形成
当堂检测
反思感悟 1.利用χ2进行独立性检验的步骤
(1)列表:列出2×2列联表;
(2)求值:求出χ2;
(3)判断:与临界值比较,作出判断.
2.独立性检验的必要性
列联表中的数据是样本数据,它只是总体的代表,它具有随机性,所以只能利用列联表的数据和等高条形图粗略判断两个分类变量是否有关系.而χ2给出了不同样本容量的数据的统一评判标准.利用它能精确判断两个分类变量是否有关系的可靠程度.
探究一
探究二
素养形成
当堂检测
变式训练为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下,认为“学生选报文、理科与对外语的兴趣有关”?
探究一
探究二
素养形成
当堂检测
解:根据题目所给的数据得到如下列联表:
根据列联表中数据由公式计算得随机变量的观测值
因为1.871×10-4<2.706,所以在犯错误的概率不超过0.1的前提下,不能认为“学生选报文、理科与对外语的兴趣有关”.
?
理科
文科
总计
有兴趣
138
73
211
无兴趣
98
52
150
总计
236
125
361
探究一
探究二
素养形成
当堂检测
独立性检验与统计的综合应用
例2为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)表1和表2分别是注射药物A和B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表
疱疹面积
[60,65)
[65,70)
[70,75)
[75,80)
频数
30
40
20
10
探究一
探究二
素养形成
当堂检测
表2:注射药物B后皮肤疱疹面积的频数分布表
完成下面2×2列联表
疱疹面积
[60,65)
[65,70)
[70,75)
[75,80)
[80,85]
频数
10
25
20
30
15
?
疱疹面积小于
70 mm2
疱疹面积不小于
70 mm2
总计
注射药物A
a=
b=
?
注射药物B
c=
d=
?
总计
?
?
n=
探究一
探究二
素养形成
当堂检测
(2)2×2列联表如下
?
疱疹面积小于
70 mm2
疱疹面积不小于
70 mm2
总计
注射药物A
a=70
b=30
100
注射药物B
c=35
d=65
100
总计
105
95
n=200
探究一
探究二
素养形成
当堂检测
反思感悟 1.独立性检验在实际中有着广泛的应用,是对实际生活中数据进行分析的一种方法,通过这种分析得出的结论对实际生活或者生产都有一定的指导作用.
2.近几年高考中较少单独考查独立性检验,经常与统计、概率等知识综合,频率分布表、频率分布直方图与独立性检验融合在一起是常见的考查形式,一般需要根据条件列出2×2列联表,计算χ2,从而解决问题.
探究一
探究二
素养形成
当堂检测
延伸探究 本例条件不变,是否有99%的把握认为注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异?
由于χ2>6.635,所以有99%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
探究一
探究二
素养形成
当堂检测
规范解答
典例 随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康情况,得到2×2列联表如下:
?
室外工作
室内工作
总计
有呼吸系统疾病
150
?
?
无呼吸系统疾病
?
100
?
总 计
200
?
?
探究一
探究二
素养形成
当堂检测
(1)补全2×2列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关?
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机地抽取两人,求两人都有呼吸系统疾病的概率.
探究一
探究二
素养形成
当堂检测
解:(1)列联表如下:
所以能在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关.
?
室外工作
室内工作
总计
有呼吸系统疾病
150
200
350
无呼吸系统疾病
50
100
150
总 计
200
300
500
探究一
探究二
素养形成
当堂检测
(3)采用分层抽样从室内工作的居民中抽取6名,其中有呼吸系统疾病的抽4人,无呼吸系统疾病的抽2人,设A为“从中随机地抽取两人,两人都有呼吸系统疾病”,则
方法点睛 (1)依题意补全列联表;(2)结合χ2公式正确求解,对说法作出判断;(3)结合概率相关知识求解.
探究一
探究二
素养形成
当堂检测
1.给出下列实际问题:
①一种药物对某种病的治愈率;②两种药物治疗同一种病是否有区别;③吸烟者得肺病的概率;④吸烟是否与性别有关系;⑤网吧与青少年的犯罪是否有关系.其中用独立性检验可以解决的问题有( )
A.①②③ B.②④⑤
C.②③④⑤ D.①②③④⑤
解析:独立性检验是判断两个分类变量是否有关系的方法,而①③都是概率问题,不能用独立性检验解决.
答案:B
探究一
探究二
素养形成
当堂检测
2.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
下列叙述中,正确的是( )
A.有99%的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”
B.有95%的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”
C.有99%的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”
D.有95%的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”
答案:D
?
认为作业多
认为作业不多
总数
喜欢玩电脑游戏
18
9
27
不喜欢玩电脑游戏
8
15
23
总数
26
24
50
探究一
探究二
素养形成
当堂检测
3.某高校《统计》课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
?
为了判断主修统计专业是否与性别有关系,根据表中的数据,得到
因为4.844>3.841,所以有 的把握判定主修统计专业与性别有关系.?
答案:95%
专业
性别
非统计专业
统计专业
男
13
10
女
7
20
探究一
探究二
素养形成
当堂检测
4.调查者通过询问72名男、女大学生在购买食品时是否看营养说明得到的数据如下表所示:
大学生的性别和是否看营养说明之间 (填“有”或“没有”)关系.?
答案:有
?
看营养说明
不看营养说明
总计
男大学生
28
8
36
女大学生
16
20
36
总计
44
28
72
