人教B版(2019)高中数学选择性必修第二册 3.3 第二课时 二项式系数的性质与杨辉三角(共31张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第二册 3.3 第二课时 二项式系数的性质与杨辉三角(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览











文档简介
第二课时 二项式系数的性质与杨辉三角
课标阐释
思维脉络
1.掌握二项式系数的有关性质,并应用性质解决简单问题.
2.记住杨辉三角,会应用杨辉三角求二项式次数不大时各项的二项式系数.
激趣诱思
知识点拨
同学们根据二项式定理写出(a+b)n(n=0,1,2,3,4,5,6)的二项式系数.可以写成如下形式:
这个表早在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的仅在于这里的表是用阿拉伯数学表示,在那本书里是用汉字表示的,称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.
你能根据上述规律写出下一行的数值吗?
激趣诱思
知识点拨
杨辉三角与二项式系数的性质
因为(a+b)0=1,所以可以把n=0对应的二项式系数看成1.把n=0,1,2,3,4,5,6对应的二项式系数逐个写出,并排成如下数表形式:
激趣诱思
知识点拨
上面的二项式系数表称为“杨辉三角”或“贾宪三角”,在欧洲称为“帕斯卡三角”.
杨辉三角至少具有下面的性质:
(1)每一行都是对称的,且两端的数都是1.
激趣诱思
知识点拨
激趣诱思
知识点拨
微思考1
杨辉三角的第n行数字规律与二项展开式有何联系?
提示:杨辉三角的第n行数字规律是二项式(a+b)n-1展开式的二项式系数.
微思考2
如何求二项展开式中各项系数和或部分系数和?
提示:通常利用赋值法.
微练习
在(a+b)n的展开式中,第2项与第6项的二项式系数相等,则n=( )
A.6 B.7 C.8 D.9
答案:A
探究一
探究二
探究三
探究四
素养形成
当堂检测
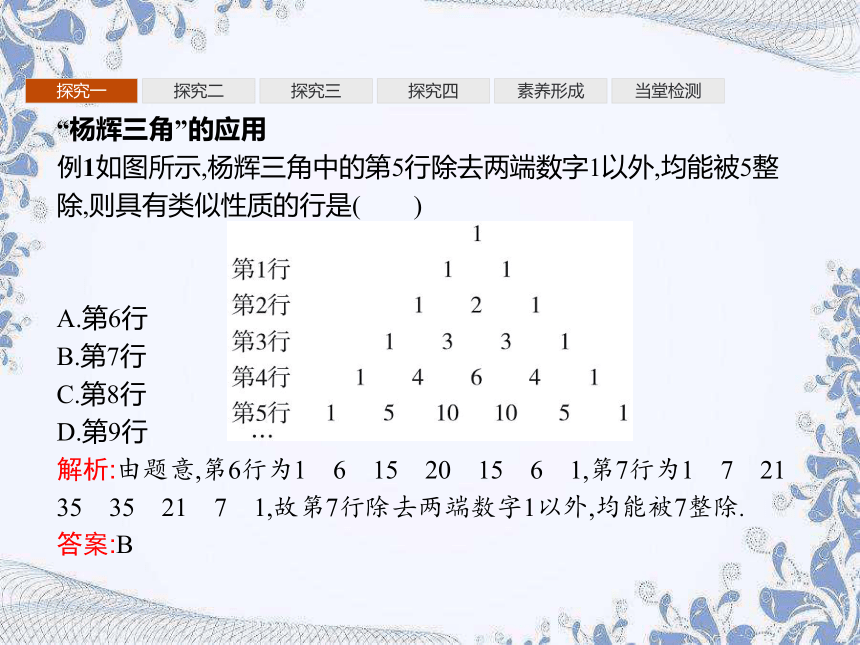
“杨辉三角”的应用
例1如图所示,杨辉三角中的第5行除去两端数字1以外,均能被5整除,则具有类似性质的行是( )
A.第6行
B.第7行
C.第8行
D.第9行
解析:由题意,第6行为1 6 15 20 15 6 1,第7行为1 7 21 35 35 21 7 1,故第7行除去两端数字1以外,均能被7整除.
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 解决与杨辉三角有关的问题的一般思路
(1)观察:对题目进行多角度观察,找出每一行的数与数之间,行与行之间的数的规律.
(2)表达:将发现的规律用数学式子表达.
(3)结论:由数学表达式得出结论.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1如图,在由二项式系数所构成的杨辉三角中,第 行中从左到右第14与第15个数的比为2∶3.?
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:34
探究一
探究二
探究三
探究四
素养形成
当堂检测
求展开式的系数和
例2设(1-2x)2 020=a0+a1x+a2x2+…+a2 020·x2 020(x∈R).
(1)求a0+a1+a2+…+a2 020的值;
(2)求a1+a3+a5+…+a2 019的值;
(3)求|a0|+|a1|+|a2|+…+|a2 020|的值.
分析先观察所求式子与展开式各项的特点,利用赋值法求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:(1)令x=1,得
a0+a1+a2+…+a2 020=(-1)2 020=1.①
(2)令x=-1,得a0-a1+a2-…-a2 019+a2 020=32 020.②
①-②得2(a1+a3+…+a2 019)=1-32 020,
∴a2k-1<0(k∈N+),a2k>0(k∈N).
∴|a0|+|a1|+|a2|+|a3|+…+|a2 019|+|a2 020|=a0-a1+a2-a3+…-a2 019+a2 020=32 020.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 1.解决二项式系数和问题的思维流程.
2.对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R,m,n∈N+)的式子求其展开式的各项系数之和,常用赋值法,只需令x=1;对(ax+by)n(a,b∈R,n∈N+)的式子求其展开式各项系数之和,只需令x=y=1.
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.一般地,若f(x)=a0+a1x+a2x2+…+anxn,则f(x)展开式中各项系数之和为f(1),
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练2已知(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,求:
(1)a0+a1+a2+a3+a4;
(2)(a0+a2+a4)2-(a1+a3)2.
解:(1)由(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,
令x=1得(2-3)4=a0+a1+a2+a3+a4,
所以a0+a1+a2+a3+a4=1.
(2)在(2x-3)4=a0+a1x+a2x2+a3x3+a4x4中,
令x=1得(2-3)4=a0+a1+a2+a3+a4,①
令x=-1得(-2-3)4=a0-a1+a2-a3+a4.②
所以(a0+a2+a4)2-(a1+a3)2
=(a0-a1+a2-a3+a4)(a0+a1+a2+a3+a4)
=(-2-3)4(2-3)4=(2+3)4(2-3)4=625.
探究一
探究二
探究三
探究四
素养形成
当堂检测
求展开式中系数或二项式系数的最大项
(1)求二项式系数最大的项;
(2)系数的绝对值最大的项是第几项?
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 二项式系数的最大项的求法
求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
(1)当n为奇数时,中间两项的二项式系数最大.
(2)当n为偶数时,中间一项的二项式系数最大.
探究一
探究二
探究三
探究四
素养形成
当堂检测
延伸探究 在本例条件下求系数最大的项与系数最小的项.
解:由本例(2)知,展开式中的第6项和第7项系数的绝对值最大,第6项的系数为负,第7项的系数为正.
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用二项式定理解整除问题及求余数问题
例4(1)用二项式定理证明1110-1能被100整除;
(2)求9192被100除所得的余数.
分析利用二项式定理证明整除问题的关键是判断所证式子与除数之间的联系,要掌握好对式子的拆分,如本例的第(1)小题,可以利用1110=(10+1)10的展开式进行证明,第(2)小题则可利用9192=(100-9)92的展开式,或利用(90+1)92的展开式进行求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 利用二项式定理可以解决求余数和整除的问题,通常需将底数化成两数的和或差的形式,且这种转化形式与除数有密切的关系.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练3(1)试求2 02060除以7所得的余数;
(2)求证:32n+2-8n-9(n∈N+)能被64整除.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用二项式定理证明不等式
先根据正整数n的最小值确定展开的最少项,然后视具体情况取定其中多少项,再结合不等式的性质和证明不等式的方法进行证明.
典例 证明:3n>(n+2)·2n-1(n∈N+,且n>2).
分析该题不等式不是一般的一元一次不等式或一元二次不等式,也不是可转化为一元一次不等式、一元二次不等式的指数不等式、对数不等式,不可能用常见不等式的证明方法处理,考虑到不等式两边均含有幂值,且底不同,可用二项式定理将两边化为同底的幂的形式进行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:因为n∈N+,且n>2,
所以3n=(2+1)n展开后至少有四项.
所以3n>(n+2)·2n-1.
方法点睛 将不等式左边3n变形为(2+1)n,将(2+1)n的二项展开式与不等式的右边对比,发现二项展开式与不等式的右边的联系.此外,决定二项式的展开式中项的取舍是证明的关键.
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.在由二项式系数所构成的杨辉三角形中,第 行中从左至右第12个数与第13个数的比为1∶2.?
答案:35
探究一
探究二
探究三
探究四
素养形成
当堂检测
4.若(2x-1)4=a0x4+a1x3+a2x2+a3x+a4,则-a0+a1-a2+a3-a4= .?
解析:令x=-1,得a0-a1+a2-a3+a4=(-3)4=81,所以-a0+a1-a2+a3-a4=-81.
答案:-81
课标阐释
思维脉络
1.掌握二项式系数的有关性质,并应用性质解决简单问题.
2.记住杨辉三角,会应用杨辉三角求二项式次数不大时各项的二项式系数.
激趣诱思
知识点拨
同学们根据二项式定理写出(a+b)n(n=0,1,2,3,4,5,6)的二项式系数.可以写成如下形式:
这个表早在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的仅在于这里的表是用阿拉伯数学表示,在那本书里是用汉字表示的,称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.
你能根据上述规律写出下一行的数值吗?
激趣诱思
知识点拨
杨辉三角与二项式系数的性质
因为(a+b)0=1,所以可以把n=0对应的二项式系数看成1.把n=0,1,2,3,4,5,6对应的二项式系数逐个写出,并排成如下数表形式:
激趣诱思
知识点拨
上面的二项式系数表称为“杨辉三角”或“贾宪三角”,在欧洲称为“帕斯卡三角”.
杨辉三角至少具有下面的性质:
(1)每一行都是对称的,且两端的数都是1.
激趣诱思
知识点拨
激趣诱思
知识点拨
微思考1
杨辉三角的第n行数字规律与二项展开式有何联系?
提示:杨辉三角的第n行数字规律是二项式(a+b)n-1展开式的二项式系数.
微思考2
如何求二项展开式中各项系数和或部分系数和?
提示:通常利用赋值法.
微练习
在(a+b)n的展开式中,第2项与第6项的二项式系数相等,则n=( )
A.6 B.7 C.8 D.9
答案:A
探究一
探究二
探究三
探究四
素养形成
当堂检测
“杨辉三角”的应用
例1如图所示,杨辉三角中的第5行除去两端数字1以外,均能被5整除,则具有类似性质的行是( )
A.第6行
B.第7行
C.第8行
D.第9行
解析:由题意,第6行为1 6 15 20 15 6 1,第7行为1 7 21 35 35 21 7 1,故第7行除去两端数字1以外,均能被7整除.
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 解决与杨辉三角有关的问题的一般思路
(1)观察:对题目进行多角度观察,找出每一行的数与数之间,行与行之间的数的规律.
(2)表达:将发现的规律用数学式子表达.
(3)结论:由数学表达式得出结论.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1如图,在由二项式系数所构成的杨辉三角中,第 行中从左到右第14与第15个数的比为2∶3.?
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:34
探究一
探究二
探究三
探究四
素养形成
当堂检测
求展开式的系数和
例2设(1-2x)2 020=a0+a1x+a2x2+…+a2 020·x2 020(x∈R).
(1)求a0+a1+a2+…+a2 020的值;
(2)求a1+a3+a5+…+a2 019的值;
(3)求|a0|+|a1|+|a2|+…+|a2 020|的值.
分析先观察所求式子与展开式各项的特点,利用赋值法求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:(1)令x=1,得
a0+a1+a2+…+a2 020=(-1)2 020=1.①
(2)令x=-1,得a0-a1+a2-…-a2 019+a2 020=32 020.②
①-②得2(a1+a3+…+a2 019)=1-32 020,
∴a2k-1<0(k∈N+),a2k>0(k∈N).
∴|a0|+|a1|+|a2|+|a3|+…+|a2 019|+|a2 020|=a0-a1+a2-a3+…-a2 019+a2 020=32 020.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 1.解决二项式系数和问题的思维流程.
2.对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R,m,n∈N+)的式子求其展开式的各项系数之和,常用赋值法,只需令x=1;对(ax+by)n(a,b∈R,n∈N+)的式子求其展开式各项系数之和,只需令x=y=1.
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.一般地,若f(x)=a0+a1x+a2x2+…+anxn,则f(x)展开式中各项系数之和为f(1),
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练2已知(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,求:
(1)a0+a1+a2+a3+a4;
(2)(a0+a2+a4)2-(a1+a3)2.
解:(1)由(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,
令x=1得(2-3)4=a0+a1+a2+a3+a4,
所以a0+a1+a2+a3+a4=1.
(2)在(2x-3)4=a0+a1x+a2x2+a3x3+a4x4中,
令x=1得(2-3)4=a0+a1+a2+a3+a4,①
令x=-1得(-2-3)4=a0-a1+a2-a3+a4.②
所以(a0+a2+a4)2-(a1+a3)2
=(a0-a1+a2-a3+a4)(a0+a1+a2+a3+a4)
=(-2-3)4(2-3)4=(2+3)4(2-3)4=625.
探究一
探究二
探究三
探究四
素养形成
当堂检测
求展开式中系数或二项式系数的最大项
(1)求二项式系数最大的项;
(2)系数的绝对值最大的项是第几项?
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 二项式系数的最大项的求法
求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
(1)当n为奇数时,中间两项的二项式系数最大.
(2)当n为偶数时,中间一项的二项式系数最大.
探究一
探究二
探究三
探究四
素养形成
当堂检测
延伸探究 在本例条件下求系数最大的项与系数最小的项.
解:由本例(2)知,展开式中的第6项和第7项系数的绝对值最大,第6项的系数为负,第7项的系数为正.
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用二项式定理解整除问题及求余数问题
例4(1)用二项式定理证明1110-1能被100整除;
(2)求9192被100除所得的余数.
分析利用二项式定理证明整除问题的关键是判断所证式子与除数之间的联系,要掌握好对式子的拆分,如本例的第(1)小题,可以利用1110=(10+1)10的展开式进行证明,第(2)小题则可利用9192=(100-9)92的展开式,或利用(90+1)92的展开式进行求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟 利用二项式定理可以解决求余数和整除的问题,通常需将底数化成两数的和或差的形式,且这种转化形式与除数有密切的关系.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练3(1)试求2 02060除以7所得的余数;
(2)求证:32n+2-8n-9(n∈N+)能被64整除.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用二项式定理证明不等式
先根据正整数n的最小值确定展开的最少项,然后视具体情况取定其中多少项,再结合不等式的性质和证明不等式的方法进行证明.
典例 证明:3n>(n+2)·2n-1(n∈N+,且n>2).
分析该题不等式不是一般的一元一次不等式或一元二次不等式,也不是可转化为一元一次不等式、一元二次不等式的指数不等式、对数不等式,不可能用常见不等式的证明方法处理,考虑到不等式两边均含有幂值,且底不同,可用二项式定理将两边化为同底的幂的形式进行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:因为n∈N+,且n>2,
所以3n=(2+1)n展开后至少有四项.
所以3n>(n+2)·2n-1.
方法点睛 将不等式左边3n变形为(2+1)n,将(2+1)n的二项展开式与不等式的右边对比,发现二项展开式与不等式的右边的联系.此外,决定二项式的展开式中项的取舍是证明的关键.
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.在由二项式系数所构成的杨辉三角形中,第 行中从左至右第12个数与第13个数的比为1∶2.?
答案:35
探究一
探究二
探究三
探究四
素养形成
当堂检测
4.若(2x-1)4=a0x4+a1x3+a2x2+a3x+a4,则-a0+a1-a2+a3-a4= .?
解析:令x=-1,得a0-a1+a2-a3+a4=(-3)4=81,所以-a0+a1-a2+a3-a4=-81.
答案:-81
