人教B版(2019)高中数学选择性必修第一册 1.2.2 空间中的平面与空间向量word含答案
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 1.2.2 空间中的平面与空间向量word含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 351.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 18:19:35 | ||
图片预览



文档简介
1.2.2 空间中的平面与空间向量
课后篇巩固提升
基础达标练
1.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( )
A.(0,1,2) B.(3,6,9)
C.(-1,-2,3) D.(3,6,8)
解析向量(1,2,3)与向量(3,6,9)共线.
答案B
2.若直线l的方向向量为a,平面α的法向量为μ,则能使l∥α的是( )
A.a=(1,0,0),μ=(-2,0,0)
B.a=(1,3,5),μ=(1,0,1)
C.a=(0,2,1),μ=(-1,0,1)
D.a=(1,-1,3),μ=(0,3,1)
解析由l∥α,故a⊥μ,即a·μ=0,故选D.
答案D
3.(多选)因为v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.n1∥n2?α∥β
B.n1⊥n2?α⊥β
C.v∥n1?l∥α
D.v⊥n1?l∥α
解析v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),
则n1∥n2?α∥β,n1⊥n2?α⊥β,,v∥n1?l⊥α,v⊥n1?l∥α或l?α.
因此AB正确.
答案AB
4.若平面α,β的法向量分别为a=(-1,2,4), b=(x,-1,-2),并且α⊥β,则x的值为( )
A.10
B.-10
C.12
D.-12
解析因为α⊥β,所以它们的法向量也互相垂直,
所以a·b=(-1,2,4)·(x,-1,-2)=0,
解得x=-10.
答案B
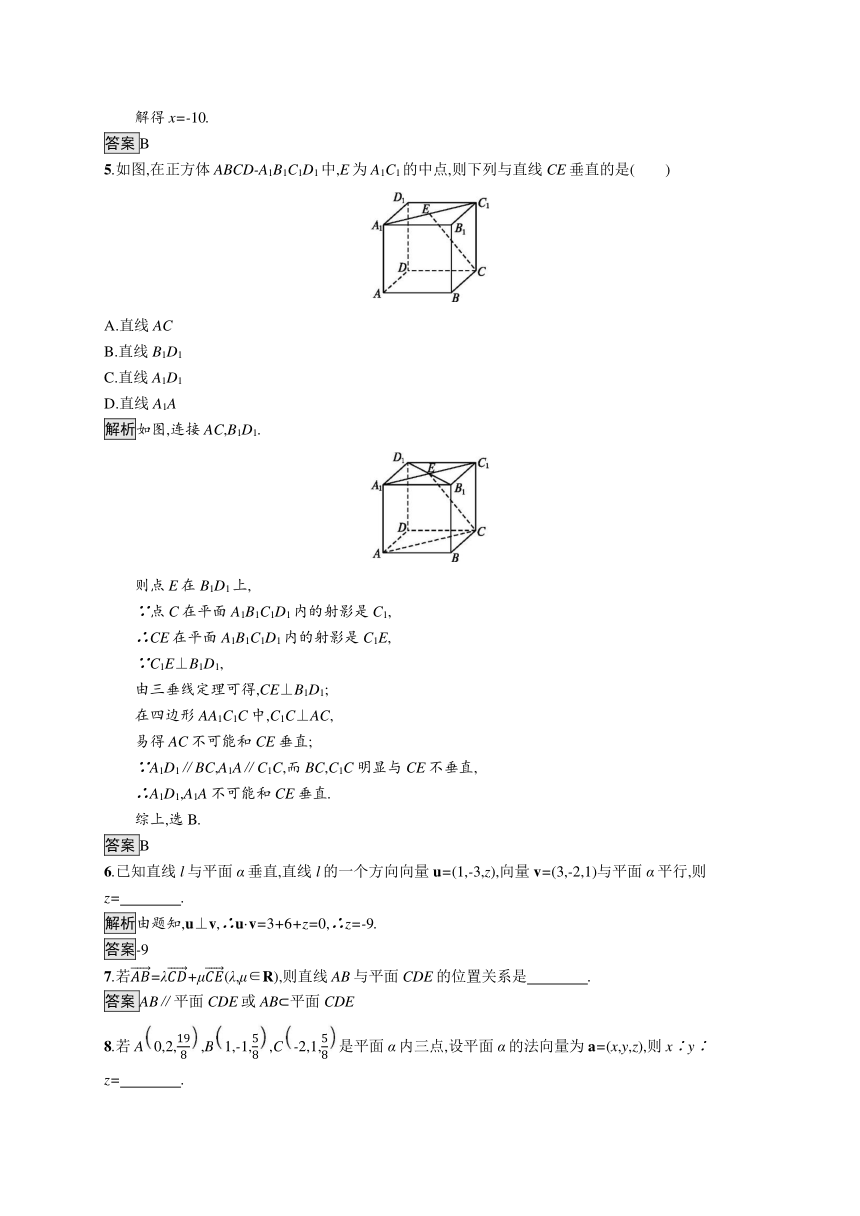
5.如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则下列与直线CE垂直的是( )
A.直线AC
B.直线B1D1
C.直线A1D1
D.直线A1A
解析如图,连接AC,B1D1.
则点E在B1D1上,
∵点C在平面A1B1C1D1内的射影是C1,
∴CE在平面A1B1C1D1内的射影是C1E,
∵C1E⊥B1D1,
由三垂线定理可得,CE⊥B1D1;
在四边形AA1C1C中,C1C⊥AC,
易得AC不可能和CE垂直;
∵A1D1∥BC,A1A∥C1C,而BC,C1C明显与CE不垂直,
∴A1D1,A1A不可能和CE垂直.
综上,选B.
答案B
6.已知直线l与平面α垂直,直线l的一个方向向量u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z= .?
解析由题知,u⊥v,∴u·v=3+6+z=0,∴z=-9.
答案-9
7.若AB=λCD+μCE(λ,μ∈R),则直线AB与平面CDE的位置关系是 .?
答案AB∥平面CDE或AB?平面CDE
8.若A0,2,198,B1,-1,58,C-2,1,58是平面α内三点,设平面α的法向量为a=(x,y,z),则x∶y∶z= .?
解析由已知得,AB=1,-3,-74,
AC=-2,-1,-74,
∵a是平面α的一个法向量,
∴a·AB=0,a·AC=0,
即x-3y-74z=0,-2x-y-74z=0,解得x=23y,z=-43y,
∴x∶y∶z=23y∶y∶-43y=2∶3∶(-4).
答案2∶3∶(-4)
9.在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:
①直线DD1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).
其中正确的是 .(填序号)?
解析DD1∥AA1,AA1=(0,0,1),故①正确;BC1∥AD1,AD1=(0,1,1),故②正确;直线AD⊥平面ABB1A1,AD=(0,1,0),故③正确;点C1的坐标为(1,1,1),AC1与平面B1CD不垂直,故④错误.
答案①②③
10.如图所示,在四棱锥S-ABCD中,底面是直角梯形,AD∥BC,∠ABC=90°,SA⊥底面ABCD,且SA=AB=BC=1,AD=12,建立适当的空间直角坐标系,求平面SCD与平面SBA的一个法向量.
解以A为坐标原点,AD,AB,AS所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),D12,0,0,C(1,1,0),S(0,0,1),
则DC=12,1,0,DS=-12,0,1,
向量AD=12,0,0是平面SBA的一个法向量.
设n=(x,y,z)为平面SCD的一个法向量,
则n·DC=12x+y=0,n·DS=-12x+z=0,
即y=-12x,z=12x.
取x=2,得y=-1,z=1,
故平面SCD的一个法向量为(2,-1,1).
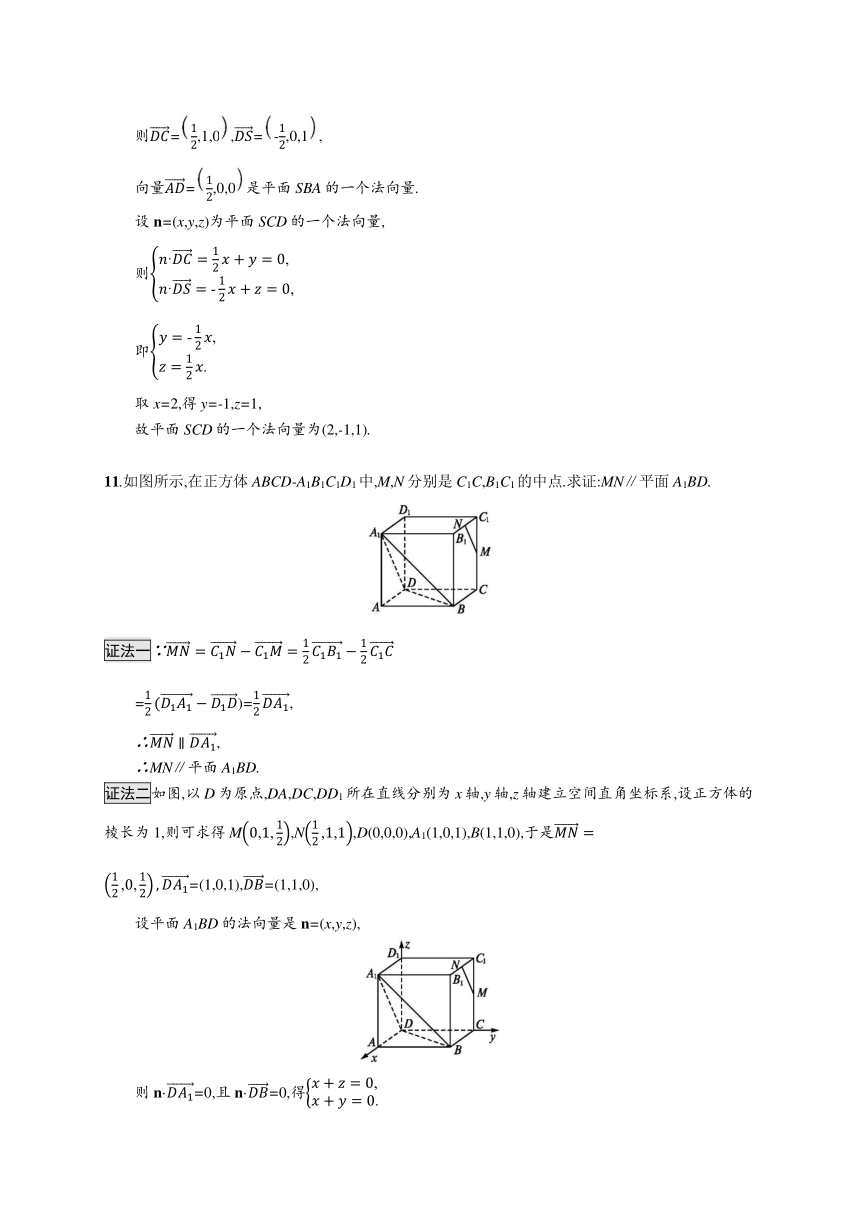
11.如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
证法一∵MN=C1N-C1M=12C1B1-12C1C
=12(D1A1-D1D)=12DA1,
∴MN∥DA1,
∴MN∥平面A1BD.
证法二如图,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设正方体的棱长为1,则可求得M0,1,12,N12,1,1,D(0,0,0),A1(1,0,1),B(1,1,0),于是MN=12,0,12,DA1=(1,0,1),DB=(1,1,0),
设平面A1BD的法向量是n=(x,y,z),
则n·DA1=0,且n·DB=0,得x+z=0,x+y=0.
取x=1,得y=-1,z=-1.∴n=(1,-1,-1).
又MN·n=12,0,12·(1,-1,-1)=0,
∴MN⊥n,且MN?平面A1BD.
∴MN∥平面A1BD.
证法三∵MN=C1N-C1M=12D1A1-12D1D
=12(DB+BA)-12(D1A1+A1D)
=12DB+12BA-12D1A1-12A1D
=12DB+12DA1+12(BA-DA)
=12DB+12DA1+12BD=12DA1.
即MN可以用DA1与DB线性表示,
∴MN与DA1,DB是共面向量,
∴MN∥平面A1BD,即MN∥平面A1BD.
12.
如图,在四棱锥P - ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
求证:(1)AE⊥CD;
(2)PD⊥平面ABE.
证明(1)∵AB,AD,AP两两垂直,∴建立如图所示的空间直角坐标系.
设PA=AB=BC=1,则P(0,0,1).
∵∠ABC=60°,
∴△ABC为正三角形.
∴C12,32,0,E14,34,12,A(0,0,0).
设D(0,y,0),AC=12,32,0,CD=-12,y-32,0.
由AC⊥CD,得AC·CD=0,
即y=233,则D0,233,0,
∴CD=-12,36,0.
又AE=14,34,12,
∴AE·CD=-12×14+36×34=0,
∴AE⊥CD,即AE⊥CD.
(2)证法一:∵AB=(1,0,0),AE=14,34,12,
∴设平面ABE的一个法向量为n=(x,y,z),
则x=0,14x+34y+12z=0,
令y=2,则z=-3,∴n=(0,2,-3).
∵PD=0,233,-1,显然PD=33n.
∴PD∥n,∴PD⊥平面ABE,即PD⊥平面ABE.
证法二:∵P(0,0,1),
∴PD=0,233,-1.
又AE·PD=34×233+12×(-1)=0,
∴PD⊥AE,即PD⊥AE.
又∵AB=(1,0,0),∴PD·AB=0,
∴PD⊥AB.又AB∩AE=A,
∴PD⊥平面ABE.
能力提升练
1.已知平面α内两向量a=(1,1,1),b=(0,2,-1),且c=ma+nb+(4,-4,1).若c为平面α的法向量,则m,n的值分别为( )
A.-1,2
B.1,-2
C.1,2
D.-1,-2
解析c=ma+nb+(4,-4,1)=(m,m,m)+(0,2n,-n)+(4,-4,1)=(m+4,m+2n-4,m-n+1),
由c为平面α的法向量,得c·a=0,c·b=0,即3m+n+1=0,m+5n-9=0,
解得m=-1,n=2.
答案A
2.已知直线l的方向向量为a,且直线l不在平面α内,平面α内两共点向量OA,OB,下列关系中一定能表示l∥α的是( )
A.a=OA B.a=kOB
C.a=pOA+λOB D.以上均不能
解析A,B,C中均能推出l∥α,或l?α,但不能确定一定能表示为l∥α.
答案D
3.如图,AO⊥平面α,垂足为点O,BC?平面α,BC⊥OB,若∠ABO=45°,∠COB=30°,则∠BAC的余弦值为( )
A.77 B.427
C.66 D.6
解析∵AO⊥平面α,BC?平面α,BC⊥OB,
由三垂线定理可得,AB⊥BC,
设OB=2.
∵∠ABO=45°,∠COB=30°,
∴AO=2,AB=22,BC=233,
在Rt△ABC中,AB=22,BC=233,∠ABC=90°,
∴AC=(22)2+(233)?2 =2213.
∴cos∠BAC=ABAC=222213=427.
故选B.
答案B
4.(多选)在正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=23A1D,AF=13AC,则以下结论不正确的有( )
A.EF至多与A1D,AC中的一个垂直
B.EF⊥A1D,EF⊥AC
C.EF与BD1相交
D.EF与BD1异面
解析以D为坐标原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系Dxyz,设正方体的棱长为1,则A1(1,0,1),D(0,0,0),A(1,0,0),C(0,1,0),E13,0,13,F23,13,0,B(1,1,0),D1(0,0,1),
∴A1D=(-1,0,-1),AC=(-1,1,0),
EF=13,13,-13,BD1=(-1,-1,1),
∴EF=-13BD1,A1D·EF=0,AC·EF=0,
从而EF∥BD1,EF⊥A1D,EF⊥AC.
答案ACD
5.
如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF∶FD的比值为( )
A.1∶2 B.1∶1 C.3∶1 D.2∶1
解析以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Axyz,
设正方形边长为1,PA=a,
则B(1,0,0),E12,1,0,P(0,0,a).
设点F的坐标为(0,y,0),
则BF=(-1,y,0),PE=12,1,-a.
因为BF⊥PE,所以BF·PE=0,
解得y=12,即点F的坐标为0,12,0,
所以F为AD的中点,所以AF∶FD=1∶1.
答案B
6.在空间直角坐标系Oxyz中,已知平面α的一个法向量是n=(1,-1,2),且平面α过点A(0,3,1).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是 .?
解析由题意知AP·n=0,且AP=(x,y-3,z-1),则(x,y-3,z-1)·(1,-1,2)=0.
化简得,x-y+2z+1=0.
答案x-y+2z+1=0
7.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n与平面ABC垂直,且|n|=21,则n的坐标为 .?
解析据题意,得AB=(-1,-1,2),AC=(1,0,2).
设n=(x,y,z),∵n与平面ABC垂直,
∴n·AB=0,n·AC=0,即-x-y+2z=0,x+2z=0,
可得x=-y2,z=y4.
∵|n|=21,∴x2+y2+z2 =21,
解得y=4或y=-4.
当y=4时,x=-2,z=1;当y=-4时,x=2,z=-1.
∴n的坐标为(-2,4,1)或(2,-4,-1).
答案(-2,4,1)或(2,-4,-1)
8.如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N,Q分别是PC,AB,CD的中点.
求证:(1)MN∥平面PAD;
(2)平面QMN∥平面PAD.
证明(1)如图,以A为原点,以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
设B(b,0,0),D(0,d,0),P(0,0,d),则C(b,d,0),
因为M,N,Q分别是PC,AB,CD的中点,
所以Mb2,d2,d2,Nb2,0,0,Qb2,d,0,
所以MN=0,-d2,-d2.因为平面PAD的一个法向量为m=(1,0,0),
且MN·m=0,即MN⊥m.又MN不在平面PAD内,故MN∥平面PAD.
(2)因为QN=(0,-d,0),
所以QN·m=0,即QN⊥m,
又QN不在平面PAD内,所以QN∥平面PAD.
又因为MN∩QN=N,所以平面MNQ∥平面PAD.
9.如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=2.
证明:A1C⊥平面BB1D1D.
证明由题设易知OA,OB,OA1两两垂直,以O为坐标原点建立空间直角坐标系,如图所示,
∵AB=AA1=2,
∴OA=OB=OA1=1,
∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),A1(0,0,1).
∴A1C=(-1,0,-1),BD=(0,-2,0),
BB1=AA1=(-1,0,1),∴A1C·BD=0,A1C·BB1=0,
∴A1C⊥BD,A1C⊥BB1,又BD∩BB1=B,
∴A1C⊥平面BB1D1D.
素养培优练
1.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,过动点P(1,2),法向量为n=(-2,3)的直线的点法式方程为-2(x-1)+3(y-2)=0,化简得2x-3y+4=0,类比上述方法,在空间直角坐标系中,经过点P(1,2,-1),且法向量为n=(-2,3,1)的平面的点法式方程应为( )
A.2x-3y+z+5=0
B.2x-3y-z+3=0
C.2x+3y+z-7=0
D.2x+3y-z-9=0
解析通过类比,易得点法式方程为
-2(x-1)+3(y-2)+(z+1)=0,
整理可得2x-3y-z+3=0,故选B.
答案B
2.在正方体ABCD-A1B1C1D1中,E,F分别为棱BB1和DD1的中点.
(1)求证:平面B1FC1∥平面ADE;
(2)试在棱DC上求一点M,使D1M⊥平面ADE.
(1)证明建立如图所示的空间直角坐标系,设正方体的棱长为2,则A(2,0,0),D(0,0,0),E(2,2,1),F(0,0,1),C1(0,2,2),B1(2,2,2).
则AE=(0,2,1),DA=(2,0,0),FC1=(0,2,1),C1B1=(2,0,0),
∴AE=FC1,DA=C1B1.
∴可得AD∥平面FB1C1,AE∥平面FB1C1.
又AD∩AE=A,
∴平面ADE∥平面FB1C1.
(2)解M应为DC的中点.M(0,1,0),D1(0,0,2),
则D1M=(0,1,-2),DE=(2,2,1),AD=(-2,0,0).
∵D1M·DE=0,D1M·AD=0,
∴D1M⊥DE,D1M⊥AD.
∵AD,DE?平面ADE,AD∩DE=D,
∴D1M⊥平面ADE.
课后篇巩固提升
基础达标练
1.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( )
A.(0,1,2) B.(3,6,9)
C.(-1,-2,3) D.(3,6,8)
解析向量(1,2,3)与向量(3,6,9)共线.
答案B
2.若直线l的方向向量为a,平面α的法向量为μ,则能使l∥α的是( )
A.a=(1,0,0),μ=(-2,0,0)
B.a=(1,3,5),μ=(1,0,1)
C.a=(0,2,1),μ=(-1,0,1)
D.a=(1,-1,3),μ=(0,3,1)
解析由l∥α,故a⊥μ,即a·μ=0,故选D.
答案D
3.(多选)因为v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.n1∥n2?α∥β
B.n1⊥n2?α⊥β
C.v∥n1?l∥α
D.v⊥n1?l∥α
解析v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),
则n1∥n2?α∥β,n1⊥n2?α⊥β,,v∥n1?l⊥α,v⊥n1?l∥α或l?α.
因此AB正确.
答案AB
4.若平面α,β的法向量分别为a=(-1,2,4), b=(x,-1,-2),并且α⊥β,则x的值为( )
A.10
B.-10
C.12
D.-12
解析因为α⊥β,所以它们的法向量也互相垂直,
所以a·b=(-1,2,4)·(x,-1,-2)=0,
解得x=-10.
答案B
5.如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则下列与直线CE垂直的是( )
A.直线AC
B.直线B1D1
C.直线A1D1
D.直线A1A
解析如图,连接AC,B1D1.
则点E在B1D1上,
∵点C在平面A1B1C1D1内的射影是C1,
∴CE在平面A1B1C1D1内的射影是C1E,
∵C1E⊥B1D1,
由三垂线定理可得,CE⊥B1D1;
在四边形AA1C1C中,C1C⊥AC,
易得AC不可能和CE垂直;
∵A1D1∥BC,A1A∥C1C,而BC,C1C明显与CE不垂直,
∴A1D1,A1A不可能和CE垂直.
综上,选B.
答案B
6.已知直线l与平面α垂直,直线l的一个方向向量u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z= .?
解析由题知,u⊥v,∴u·v=3+6+z=0,∴z=-9.
答案-9
7.若AB=λCD+μCE(λ,μ∈R),则直线AB与平面CDE的位置关系是 .?
答案AB∥平面CDE或AB?平面CDE
8.若A0,2,198,B1,-1,58,C-2,1,58是平面α内三点,设平面α的法向量为a=(x,y,z),则x∶y∶z= .?
解析由已知得,AB=1,-3,-74,
AC=-2,-1,-74,
∵a是平面α的一个法向量,
∴a·AB=0,a·AC=0,
即x-3y-74z=0,-2x-y-74z=0,解得x=23y,z=-43y,
∴x∶y∶z=23y∶y∶-43y=2∶3∶(-4).
答案2∶3∶(-4)
9.在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:
①直线DD1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).
其中正确的是 .(填序号)?
解析DD1∥AA1,AA1=(0,0,1),故①正确;BC1∥AD1,AD1=(0,1,1),故②正确;直线AD⊥平面ABB1A1,AD=(0,1,0),故③正确;点C1的坐标为(1,1,1),AC1与平面B1CD不垂直,故④错误.
答案①②③
10.如图所示,在四棱锥S-ABCD中,底面是直角梯形,AD∥BC,∠ABC=90°,SA⊥底面ABCD,且SA=AB=BC=1,AD=12,建立适当的空间直角坐标系,求平面SCD与平面SBA的一个法向量.
解以A为坐标原点,AD,AB,AS所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),D12,0,0,C(1,1,0),S(0,0,1),
则DC=12,1,0,DS=-12,0,1,
向量AD=12,0,0是平面SBA的一个法向量.
设n=(x,y,z)为平面SCD的一个法向量,
则n·DC=12x+y=0,n·DS=-12x+z=0,
即y=-12x,z=12x.
取x=2,得y=-1,z=1,
故平面SCD的一个法向量为(2,-1,1).
11.如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
证法一∵MN=C1N-C1M=12C1B1-12C1C
=12(D1A1-D1D)=12DA1,
∴MN∥DA1,
∴MN∥平面A1BD.
证法二如图,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设正方体的棱长为1,则可求得M0,1,12,N12,1,1,D(0,0,0),A1(1,0,1),B(1,1,0),于是MN=12,0,12,DA1=(1,0,1),DB=(1,1,0),
设平面A1BD的法向量是n=(x,y,z),
则n·DA1=0,且n·DB=0,得x+z=0,x+y=0.
取x=1,得y=-1,z=-1.∴n=(1,-1,-1).
又MN·n=12,0,12·(1,-1,-1)=0,
∴MN⊥n,且MN?平面A1BD.
∴MN∥平面A1BD.
证法三∵MN=C1N-C1M=12D1A1-12D1D
=12(DB+BA)-12(D1A1+A1D)
=12DB+12BA-12D1A1-12A1D
=12DB+12DA1+12(BA-DA)
=12DB+12DA1+12BD=12DA1.
即MN可以用DA1与DB线性表示,
∴MN与DA1,DB是共面向量,
∴MN∥平面A1BD,即MN∥平面A1BD.
12.
如图,在四棱锥P - ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
求证:(1)AE⊥CD;
(2)PD⊥平面ABE.
证明(1)∵AB,AD,AP两两垂直,∴建立如图所示的空间直角坐标系.
设PA=AB=BC=1,则P(0,0,1).
∵∠ABC=60°,
∴△ABC为正三角形.
∴C12,32,0,E14,34,12,A(0,0,0).
设D(0,y,0),AC=12,32,0,CD=-12,y-32,0.
由AC⊥CD,得AC·CD=0,
即y=233,则D0,233,0,
∴CD=-12,36,0.
又AE=14,34,12,
∴AE·CD=-12×14+36×34=0,
∴AE⊥CD,即AE⊥CD.
(2)证法一:∵AB=(1,0,0),AE=14,34,12,
∴设平面ABE的一个法向量为n=(x,y,z),
则x=0,14x+34y+12z=0,
令y=2,则z=-3,∴n=(0,2,-3).
∵PD=0,233,-1,显然PD=33n.
∴PD∥n,∴PD⊥平面ABE,即PD⊥平面ABE.
证法二:∵P(0,0,1),
∴PD=0,233,-1.
又AE·PD=34×233+12×(-1)=0,
∴PD⊥AE,即PD⊥AE.
又∵AB=(1,0,0),∴PD·AB=0,
∴PD⊥AB.又AB∩AE=A,
∴PD⊥平面ABE.
能力提升练
1.已知平面α内两向量a=(1,1,1),b=(0,2,-1),且c=ma+nb+(4,-4,1).若c为平面α的法向量,则m,n的值分别为( )
A.-1,2
B.1,-2
C.1,2
D.-1,-2
解析c=ma+nb+(4,-4,1)=(m,m,m)+(0,2n,-n)+(4,-4,1)=(m+4,m+2n-4,m-n+1),
由c为平面α的法向量,得c·a=0,c·b=0,即3m+n+1=0,m+5n-9=0,
解得m=-1,n=2.
答案A
2.已知直线l的方向向量为a,且直线l不在平面α内,平面α内两共点向量OA,OB,下列关系中一定能表示l∥α的是( )
A.a=OA B.a=kOB
C.a=pOA+λOB D.以上均不能
解析A,B,C中均能推出l∥α,或l?α,但不能确定一定能表示为l∥α.
答案D
3.如图,AO⊥平面α,垂足为点O,BC?平面α,BC⊥OB,若∠ABO=45°,∠COB=30°,则∠BAC的余弦值为( )
A.77 B.427
C.66 D.6
解析∵AO⊥平面α,BC?平面α,BC⊥OB,
由三垂线定理可得,AB⊥BC,
设OB=2.
∵∠ABO=45°,∠COB=30°,
∴AO=2,AB=22,BC=233,
在Rt△ABC中,AB=22,BC=233,∠ABC=90°,
∴AC=(22)2+(233)?2 =2213.
∴cos∠BAC=ABAC=222213=427.
故选B.
答案B
4.(多选)在正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=23A1D,AF=13AC,则以下结论不正确的有( )
A.EF至多与A1D,AC中的一个垂直
B.EF⊥A1D,EF⊥AC
C.EF与BD1相交
D.EF与BD1异面
解析以D为坐标原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系Dxyz,设正方体的棱长为1,则A1(1,0,1),D(0,0,0),A(1,0,0),C(0,1,0),E13,0,13,F23,13,0,B(1,1,0),D1(0,0,1),
∴A1D=(-1,0,-1),AC=(-1,1,0),
EF=13,13,-13,BD1=(-1,-1,1),
∴EF=-13BD1,A1D·EF=0,AC·EF=0,
从而EF∥BD1,EF⊥A1D,EF⊥AC.
答案ACD
5.
如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF∶FD的比值为( )
A.1∶2 B.1∶1 C.3∶1 D.2∶1
解析以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Axyz,
设正方形边长为1,PA=a,
则B(1,0,0),E12,1,0,P(0,0,a).
设点F的坐标为(0,y,0),
则BF=(-1,y,0),PE=12,1,-a.
因为BF⊥PE,所以BF·PE=0,
解得y=12,即点F的坐标为0,12,0,
所以F为AD的中点,所以AF∶FD=1∶1.
答案B
6.在空间直角坐标系Oxyz中,已知平面α的一个法向量是n=(1,-1,2),且平面α过点A(0,3,1).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是 .?
解析由题意知AP·n=0,且AP=(x,y-3,z-1),则(x,y-3,z-1)·(1,-1,2)=0.
化简得,x-y+2z+1=0.
答案x-y+2z+1=0
7.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n与平面ABC垂直,且|n|=21,则n的坐标为 .?
解析据题意,得AB=(-1,-1,2),AC=(1,0,2).
设n=(x,y,z),∵n与平面ABC垂直,
∴n·AB=0,n·AC=0,即-x-y+2z=0,x+2z=0,
可得x=-y2,z=y4.
∵|n|=21,∴x2+y2+z2 =21,
解得y=4或y=-4.
当y=4时,x=-2,z=1;当y=-4时,x=2,z=-1.
∴n的坐标为(-2,4,1)或(2,-4,-1).
答案(-2,4,1)或(2,-4,-1)
8.如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N,Q分别是PC,AB,CD的中点.
求证:(1)MN∥平面PAD;
(2)平面QMN∥平面PAD.
证明(1)如图,以A为原点,以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
设B(b,0,0),D(0,d,0),P(0,0,d),则C(b,d,0),
因为M,N,Q分别是PC,AB,CD的中点,
所以Mb2,d2,d2,Nb2,0,0,Qb2,d,0,
所以MN=0,-d2,-d2.因为平面PAD的一个法向量为m=(1,0,0),
且MN·m=0,即MN⊥m.又MN不在平面PAD内,故MN∥平面PAD.
(2)因为QN=(0,-d,0),
所以QN·m=0,即QN⊥m,
又QN不在平面PAD内,所以QN∥平面PAD.
又因为MN∩QN=N,所以平面MNQ∥平面PAD.
9.如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=2.
证明:A1C⊥平面BB1D1D.
证明由题设易知OA,OB,OA1两两垂直,以O为坐标原点建立空间直角坐标系,如图所示,
∵AB=AA1=2,
∴OA=OB=OA1=1,
∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),A1(0,0,1).
∴A1C=(-1,0,-1),BD=(0,-2,0),
BB1=AA1=(-1,0,1),∴A1C·BD=0,A1C·BB1=0,
∴A1C⊥BD,A1C⊥BB1,又BD∩BB1=B,
∴A1C⊥平面BB1D1D.
素养培优练
1.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,过动点P(1,2),法向量为n=(-2,3)的直线的点法式方程为-2(x-1)+3(y-2)=0,化简得2x-3y+4=0,类比上述方法,在空间直角坐标系中,经过点P(1,2,-1),且法向量为n=(-2,3,1)的平面的点法式方程应为( )
A.2x-3y+z+5=0
B.2x-3y-z+3=0
C.2x+3y+z-7=0
D.2x+3y-z-9=0
解析通过类比,易得点法式方程为
-2(x-1)+3(y-2)+(z+1)=0,
整理可得2x-3y-z+3=0,故选B.
答案B
2.在正方体ABCD-A1B1C1D1中,E,F分别为棱BB1和DD1的中点.
(1)求证:平面B1FC1∥平面ADE;
(2)试在棱DC上求一点M,使D1M⊥平面ADE.
(1)证明建立如图所示的空间直角坐标系,设正方体的棱长为2,则A(2,0,0),D(0,0,0),E(2,2,1),F(0,0,1),C1(0,2,2),B1(2,2,2).
则AE=(0,2,1),DA=(2,0,0),FC1=(0,2,1),C1B1=(2,0,0),
∴AE=FC1,DA=C1B1.
∴可得AD∥平面FB1C1,AE∥平面FB1C1.
又AD∩AE=A,
∴平面ADE∥平面FB1C1.
(2)解M应为DC的中点.M(0,1,0),D1(0,0,2),
则D1M=(0,1,-2),DE=(2,2,1),AD=(-2,0,0).
∵D1M·DE=0,D1M·AD=0,
∴D1M⊥DE,D1M⊥AD.
∵AD,DE?平面ADE,AD∩DE=D,
∴D1M⊥平面ADE.
